11.2 Modèle sans interactions

La version la plus simple consiste à considérer simplement deux facteurs successivement, c’est-à-dire que la variance est décomposée d’abord selon le premier facteur, et ensuite selon le second.

\[y_{ijk} = \mu + \tau1_j + \tau2_k + \epsilon_i \mathrm{\ avec\ } \epsilon \sim N(0, \sigma)\]

avec \(\tau1_j\) correspondant à l’écart de la moyenne générale \(µ\) à la moyenne selon la j^ème population pour la variable fact1, et \(\tau2_k\) correspondant à l’écart vers le k^ème niveau d’une seconde variable fact2. La formule qui spécifie ce modèle dans R avec les trois variables y, fact1 et fact2 s’écrit :

\[y \sim fact1 + fact2\]

Notez que, quel que soit le niveau considéré pour \(\tau1\), un niveau donné de \(\tau2\) est constant dans l’équation qui décrit ce modèle. Cela signifie que l’on considère que les écarts pour les moyennes de la variable fact2 sont toujours les mêmes depuis les moyennes de fact1. Donc, si une sous-population de fact2 tend à avoir une moyenne, disons, supérieure pour la première sous-population de fact1, elle sera considérée comme ayant les mêmes écarts pour toutes les autres sous-populations de fact1. Évidemment, cette condition n’est pas toujours rencontrée dans la pratique. Le graphique des interactions (Fig. 11.1) permets de visualiser les écarts des moyennes respectives des différentes sous-populations. Si les segments de droites sont parallèles ou presque parallèles, nous pouvons considérer que les interactions sont faibles, voire nulles, et le présent modèle sera adapté.

read("crabs", package = "MASS", lang = "fr") %>.%
  mutate(., aspect = labelise(
    as.numeric(rear / width),
    "Ratio largeur arrière / max", units = NA)) %>.%
  mutate(., aspect5 = labelise(
    aspect^5,
    "(Ratio largeur arrière /max)^5", units = NA)) %>.%
  select(., species, sex, aspect, aspect5) %->%
  crabs2
# Graphique de base pour visualiser les interactions
#chart$base(interaction.plot(crabs2$species, crabs2$sex, crabs2$aspect5))
# Version avec ggplot2
crabs2 %>.%
  sgroup_by(., species, sex) %>.%
  ssummarise(., aspect5_groups = mean(aspect5)) %>.%
  print(.) %>.% # Tableau des moyennes par groupes
  chart(data = ., aspect5_groups ~ species %col=% sex %group=% sex) +
    geom_line() +
    geom_point()

# # A data.table: 4 x 3
#   species sex   aspect5_groups
#   <fct>   <fct>          <dbl>
# 1 B       F            0.00727
# 2 B       M            0.00363
# 3 O       F            0.00811
# 4 O       M            0.00427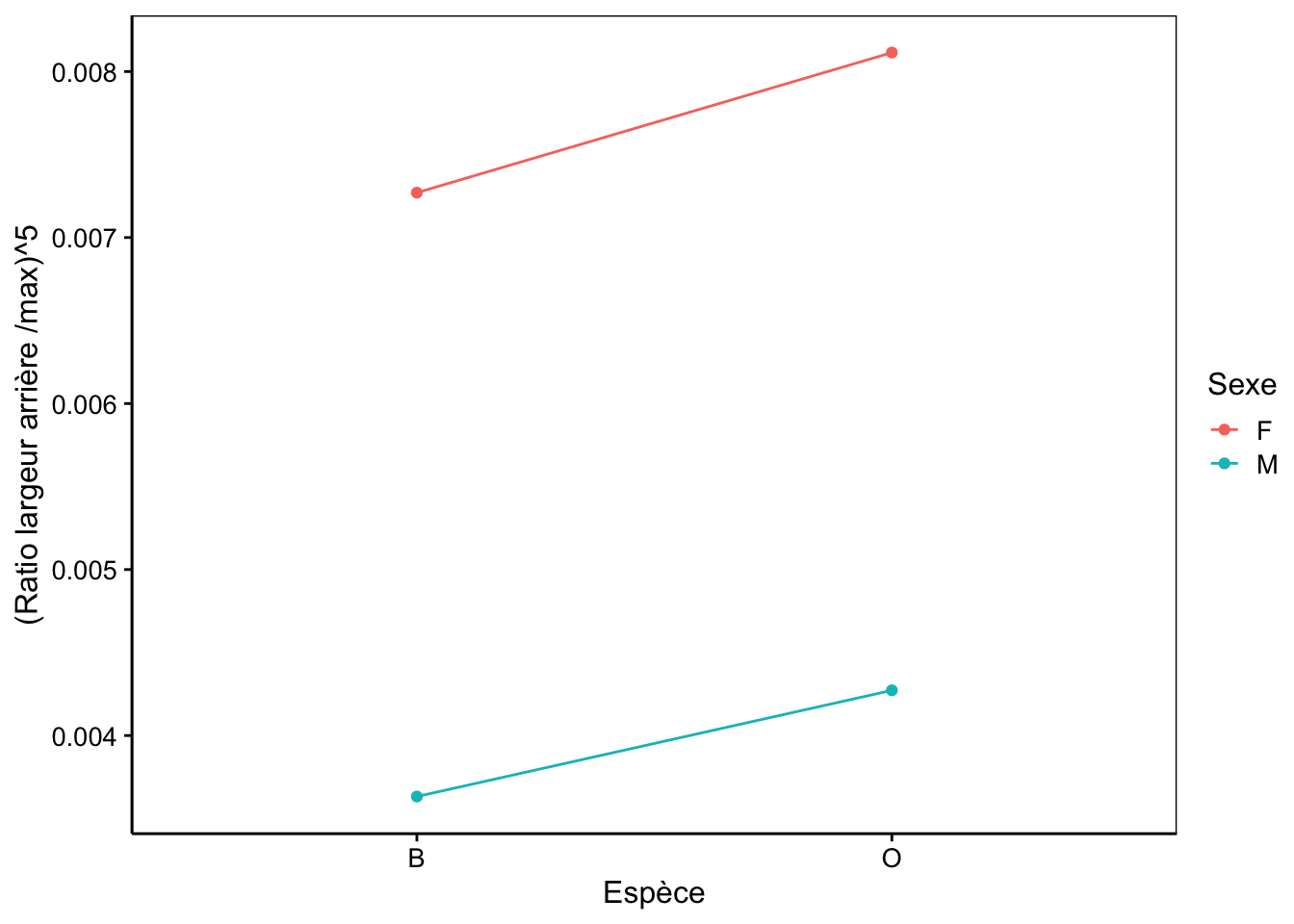

Graphique des interactions entre les variables facteurs (espèce et sexe). Les traits (pratiquement) parallèles indiquent qu'il n'y a pas d'interactions, comme c'est le cas ici.

Figure 11.1: Graphique des interactions entre les variables facteurs (espèce et sexe). Les traits (pratiquement) parallèles indiquent qu’il n’y a pas d’interactions, comme c’est le cas ici.

À vous de jouer !

Au niveau de la description préliminaire des données, nous pourrons utiliser un tableau qui résume la moyenne, l’écart type et le nombre d’observations pour chaque combinaison des deux variables facteurs.

crabs2 %>.%
  sgroup_by(., species, sex) %>.%
  ssummarise(.,
    mean  = fmean(aspect5),
    sd    = fsd(aspect5),
    count = fnobs(aspect5))

# # A data.table: 4 x 5
#   species sex      mean      sd count
#   <fct>   <fct>   <dbl>   <dbl> <int>
# 1 B       F     0.00727 0.00115    50
# 2 B       M     0.00363 0.00124    50
# 3 O       F     0.00811 0.00138    50
# 4 O       M     0.00427 0.00130    50

Pour la visualisation graphique, nous sommes tributaires du nombre d’observations. Avec moins d’une petite dizaine d’observations, nous représenterons des points pour chaque observation et superposerons les moyennes. Lorsque le nombre est plus grand, nous pourrons utiliser soit les boites de dispersion, soit le graphique en violon si ce nombre est encore plus élevé. Voyons cela sur notre exemple. La Fig. 11.2 montre ce que cela donne si l’on opte pour les boites de dispersion.

chart(data = crabs2, aspect5 ~ species | sex) +
  geom_boxplot()

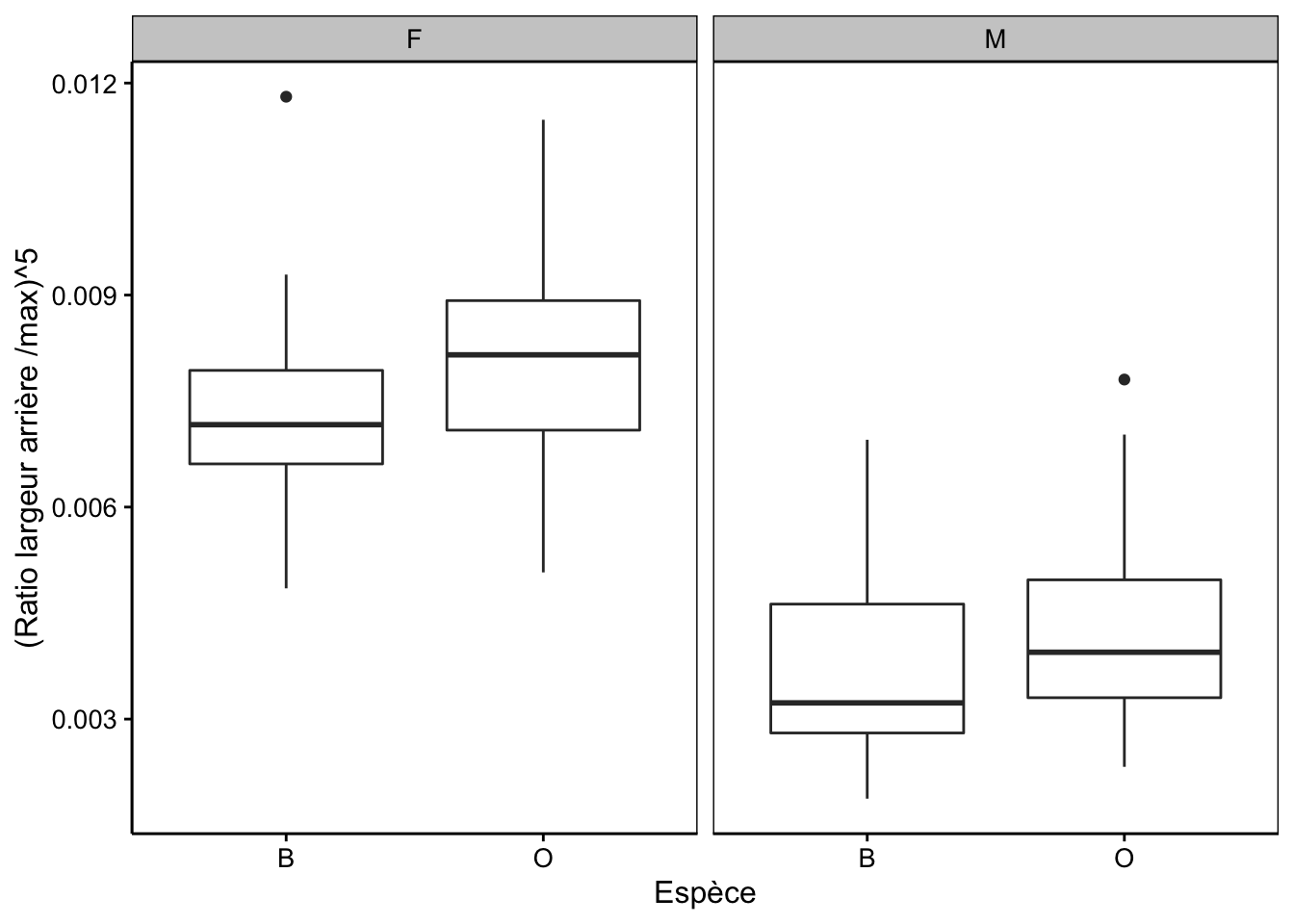
Figure 11.2: Taille relative de la carapace à l’arrière de crabes L. variegatus (deux variétés et deux sexes), version simple.

La Fig. 11.3 est une version améliorée avec les observations et les moyennes pour chaque sous-groupe ajouté au graphique selon la même technique que nous avions utilisée pour l’ANOVA à un facteur.

chart(data = crabs2, aspect5 ~ species | sex) +
  geom_boxplot() +
  geom_jitter(width = 0.05, alpha = 0.3) +
  stat_summary(geom = "point", fun = "mean", color = "red", size = 3)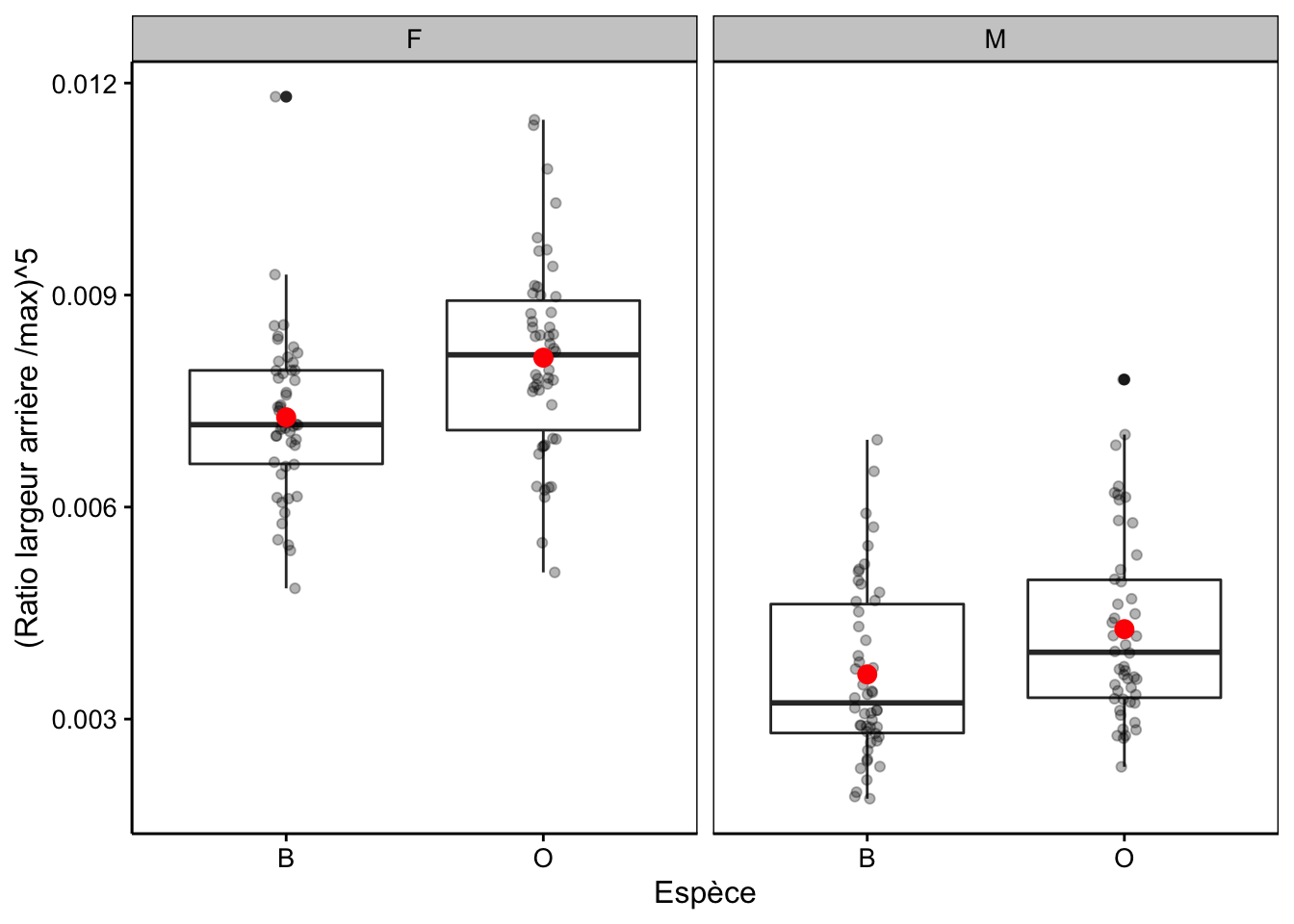

Figure 11.3: Taille relative de la carapace à l’arrière de crabes L. variegatus (deux variétés et deux sexes), version annotée.

Maintenant que nous avons décrit correctement nos données par rapport à l’analyse que nous souhaitons faire, nous pouvons réaliser notre ANOVA à deux facteurs. Nous devons vérifier l’homoscédasticité, mais le test de Bartlett que nous réalisons revient au même que celui que nous avons fait en décomposant toutes les sous-populations. Comme nous n’avons pas nécessairement ce calcul réalisé (la variable group que nous avions calculée au module 10), nous utilisons la fonction interaction() qui effectue ce calcul pour nous directement dans la formule :

bartlett.test(data = crabs2, aspect5 ~ interaction(species, sex))

# 
#   Bartlett test of homogeneity of variances
# 
# data:  aspect5 by interaction(species, sex)
# Bartlett's K-squared = 1.7948, df = 3, p-value = 0.6161

À vous de jouer !

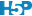
Si vous comparez avec le test que nous avions fait dans le cas de l’ANOVA à un facteur sur la variable group, vous constaterez qu’il donne exactement le même résultat. Nous continuons avec notre ANOVA.

anova(crabs2_anova2 <- lm(data = crabs2, aspect5 ~ species + sex))

# Analysis of Variance Table
# 
# Response: aspect5
#            Df     Sum Sq    Mean Sq F value    Pr(>F)    
# species     1 0.00002753 0.00002753   17.15  5.12e-05 ***
# sex         1 0.00069935 0.00069935  435.66 < 2.2e-16 ***
# Residuals 197 0.00031624 0.00000161                      
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Comme la variance est décomposée en trois étapes (selon l’espèce, puis selon le sexe, puis les résidus), nous avons trois lignes dans le tableau de l’ANOVA. Nous effectuons deux tests. Le premier consiste à comparer les carrés moyens (Mean Sq) pour l’espèce par rapport aux résidus, lignes 1 et 3. Donc, la valeur F (F value) est le ratio de la somme des carrés species divisé par la somme des carrés des résidus (0.0000275 / 0.00000161 = 17,1), et cette valeur est reportée sur la loi de distribution théorique F pour obtenir une première valeur P (ici 5,12 . 10^-5). De même, le second test qui s’intéresse au sexe calcule la valeur F via le ratio de la somme des carrés pour sex divisé par la somme des carrés des résidus (lignes 2 et 3, 0.000700 / 0.00000161 = 434,7), et la loi F nous permet de calculer une valeur P pour ce second test (ici 2,2 . 10^-16).

Nous interprétons chacun des deux tests séparément. Dans notre cas, nous pouvons dire avec un seuil \(\alpha\) de 5% que nous rejetons \(H_0\) dans les deux cas (P < \(\alpha\)). Donc le rapport largeur arrière sur largeur max de la carapace (à la puissance 5) est significativement différent au seuil \(\alpha\) de 5% à la fois en fonction de l’espèce (F = 17,15, ddl = 1 et 197, valeur P << 0,001) et du sexe (F = 436, ddl = 1 et 197, valeur P << 0,001)⁴⁷.

La suite logique consiste à réaliser des tests “post hoc”. Ils ne sont pas vraiment nécessaires ici puisque nous n’avons que deux niveaux pour chacune des deux variables, mais nous les réalisons quand même pour montrer le code correspondant.

summary(crabs2_posthoc2 <- confint(multcomp::glht(crabs2_anova2,
  linfct = multcomp::mcp(species = "Tukey", sex = "Tukey"))))

# 
#    Simultaneous Tests for General Linear Hypotheses
# 
# Multiple Comparisons of Means: Tukey Contrasts
# 
# 
# Fit: lm(formula = aspect5 ~ species + sex, data = crabs2)
# 
# Linear Hypotheses:
#                       Estimate Std. Error t value Pr(>|t|)    
# species: O - B == 0  0.0007420  0.0001792   4.141 0.000102 ***
# sex: M - F == 0     -0.0037399  0.0001792 -20.872  < 1e-10 ***
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# (Adjusted p values reported -- single-step method)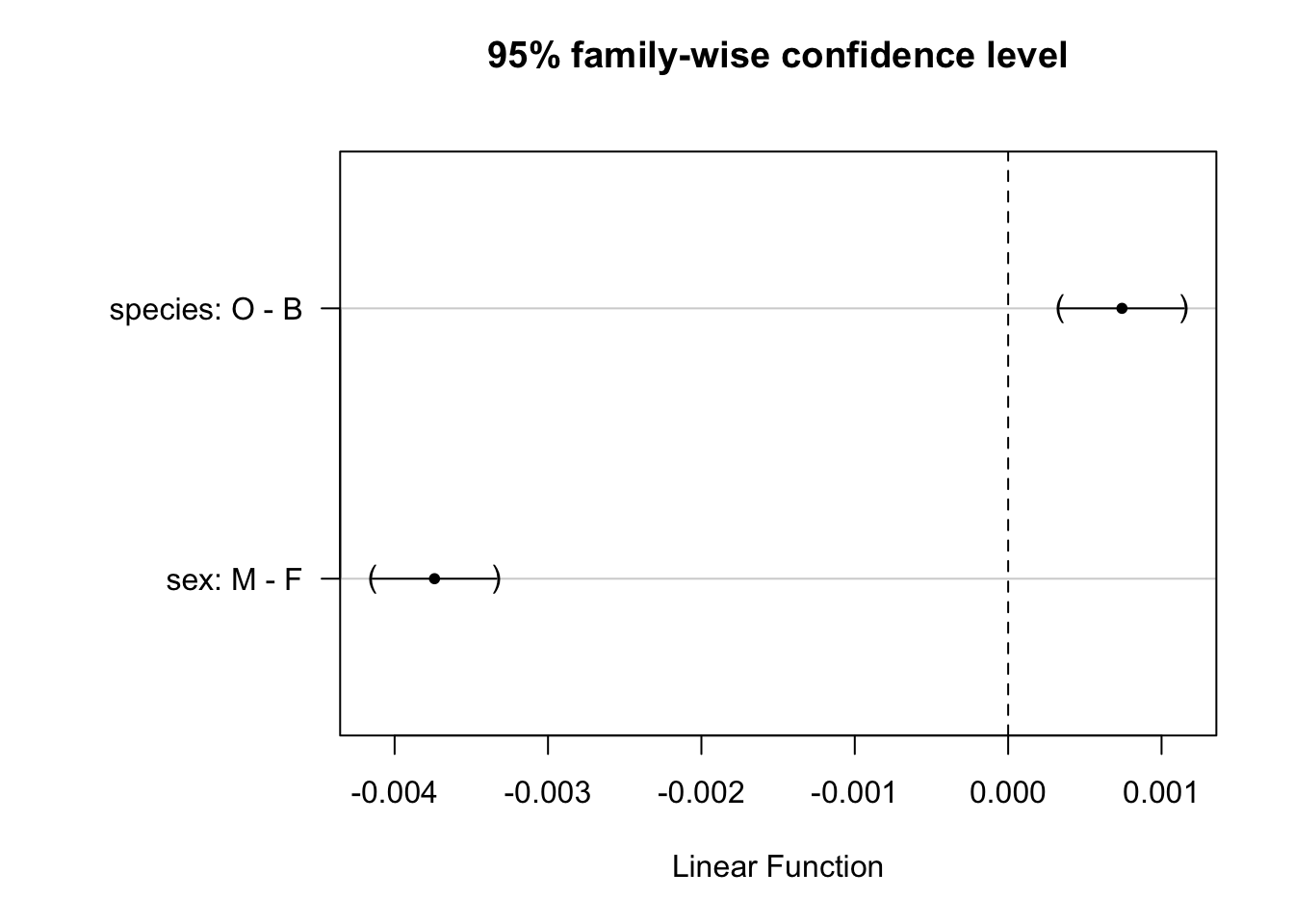

oma <- par(oma = c(0, 5.1, 0, 0))
plot(crabs2_posthoc2)

par(oma)
rm(oma)

Ceci confirme que les différences sont significatives au seuil \(\alpha\) de 5% puisque les valeurs P pour les comparaisons deux à deux sont inférieures à \(\alpha\) et les intervalles de confiance sur le graphique ne contiennent pas zéro. Il ne nous reste plus qu’à vérifier la distribution des résidus de l’ANOVA pour que notre analyse soit complète (Fig. 11.4).

Figure 11.4: Graphique quantile-quantile des résidus pour l’ANOVA à deux facteurs sans interactions de aspect^5.

Encore une fois, nous voyons que les résidus sont quasiment les mêmes que précédemment, mais cela n’aurait pas été le cas si des interactions étaient présentes. La distribution s’éloigne un peu d’une Gaussienne pour les valeurs élevées surtout. Mais comme l’ANOVA est robuste à ce critère, et que l’homoscédasticité a été vérifiée sur la transformation puissance 5 de notre variable, nous pouvons conserver notre analyse moyennant une précaution supplémentaire : vérifier que les valeurs P sont beaucoup plus petites que notre seuil comme sécurité supplémentaires contre les approximations liées à la légère violation de la contrainte de distribution normale des résidus. C’est le cas ici, et nous pouvons donc conclure notre analyse.

Conditions d’application

échantillon représentatif (par exemple, aléatoire),
observations indépendantes,
variable réponse quantitative,
deux variables explicatives qualitatives à deux niveaux ou plus,
distribution normale des résidus \(\epsilon_i\),
homoscédasticité (même variance intragroupes),
pas d’interactions entre les deux variables explicatives.

Notez que si vous incluez le tableau de l’ANOVA dans votre rapport ou dans une publication, il n’est pas nécessaire de répéter les résultats des tests entre parenthèses. Vous pouvez juste vous référer au tableau en question.↩︎