7.3 Distribution uniforme
La loi de la distribution uniforme se rapporte à un mécanisme qui génère tous les évènements de manière équiprobable.
7.3.1 Distribution discrète
Dans le cas d’évènements discrets, si \(n_E\) est le nombre total d’évènements possibles, la probabilité d’un de ces évènements vaut donc :
\[\mathrm{P}(E) = \frac{1}{n_E}\]
La distribution uniforme est d’application pour les jeux de hasard (dés, boules de loto …). En biologie, elle est plus rare. Dans le cas d’un sexe-ratio de 1:1 (autant de mâles que de femelles), la probabilité qu’un nouveau-né soit un mâle ou une femelle suit une distribution uniforme et vaut 1/2. La distribution spatiale des individus dans une population biologique peut être uniforme lorsque les individus interagissent de telle manière que la distance entre eux soit identique (par exemple, dans un groupe de manchots Aptenodytes patagonicus sur la banquise). Imaginons un animal hypothétique pour lequel la portée peut être de 1 à 4 petits de manière équiprobable. Nous avons alors 1/4 des portées qui présentent respectivement, 1, 2, 3 ou 4 petits (Fig. 7.1).
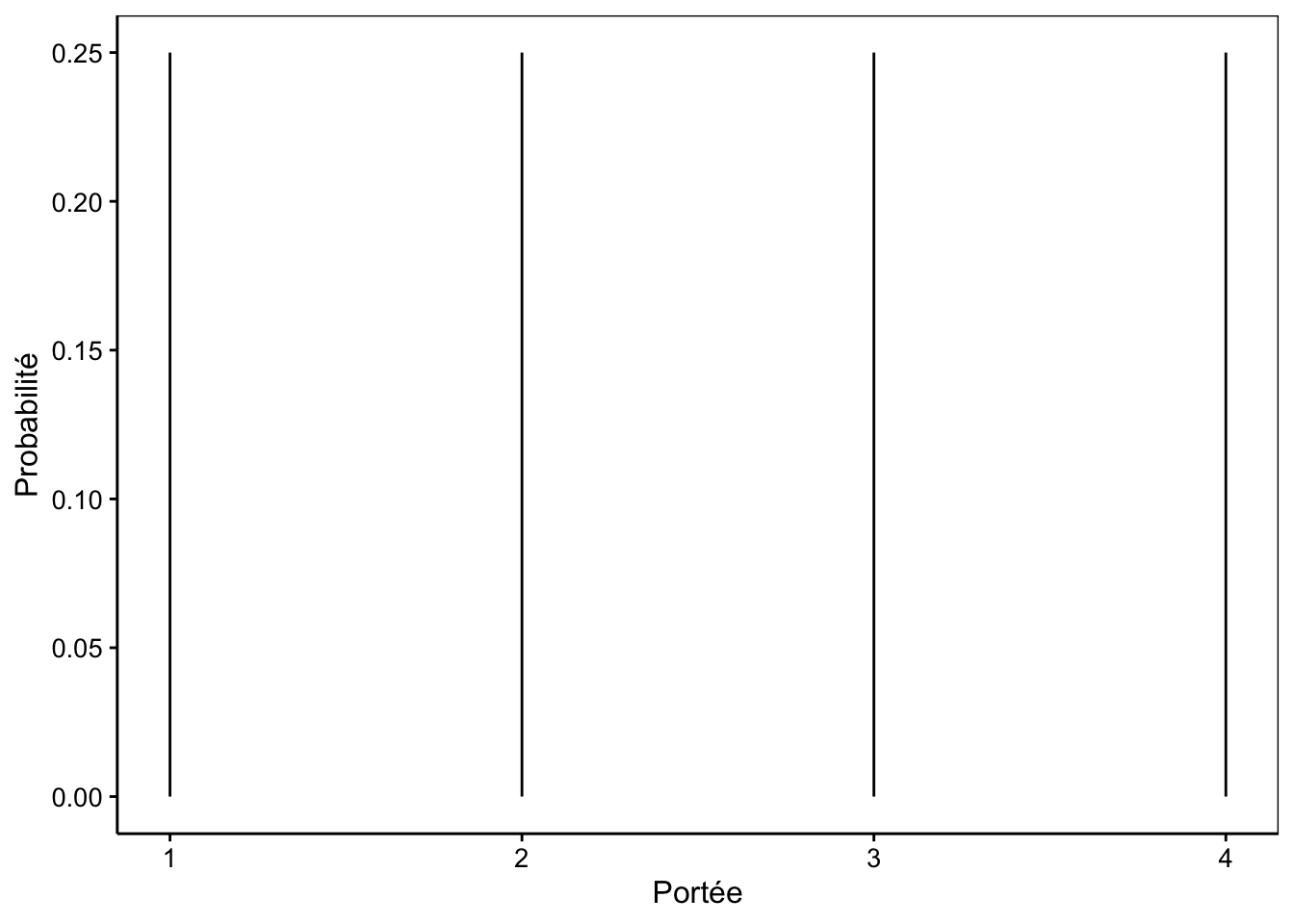
Figure 7.1: Probabilité du nombre de petits dans une portée qui suivrait un distribution strictement uniforme entre 1 et 4.
7.3.2 Distribution continue
Nous avons déjà évoqué le fait que les probabilités issues de distributions continues ne se traitent pas comme celles de probabilités discrètes. Il est maintenant temps d’approfondir la question. Considérons une distribution uniforme discrète, admettant donc un très grand nombre d’évènements équiprobables (avec ce nombre tendant vers l’infini). Donc, la probabilité de chaque évènement est un divisé par le nombre d’évènements possibles \(n_E = \infty\) :
\[\mathrm{P}(E) = \frac{1}{n_E} = \frac{1}{\infty} = 0\]
… et ce calcul est correct ! Il correspond d’ailleurs au résultat pour une loi de distribution continue.
Dans le cas de probabilités continues, la probabilité d’un évènement en particulier est toujours nulle. Nous pouvons seulement calculer que l’un parmi plusieurs évènements se produise (compris dans un intervalle).
La représentation graphique d’une loi de distribution continue est un outil utile pour la comprendre et vérifier ses calculs. La forme la plus courante consiste à montrer la courbe de densité de probabilité pour une distribution continue. Sur l’axe X, nous avons les quantiles (les valeurs observables), et sur l’axe Y, la densité de probabilité28. Par exemple, si nous constatons qu’un insecte butineur arrive sur une fleur en moyenne toutes les 4 minutes, la probabilité qu’un butineur arrive dans un intervalle de temps compris entre 0 et 4 min depuis le moment initial \(t_0\) de nos observations suit une distribution uniforme continue (Fig. 7.2).
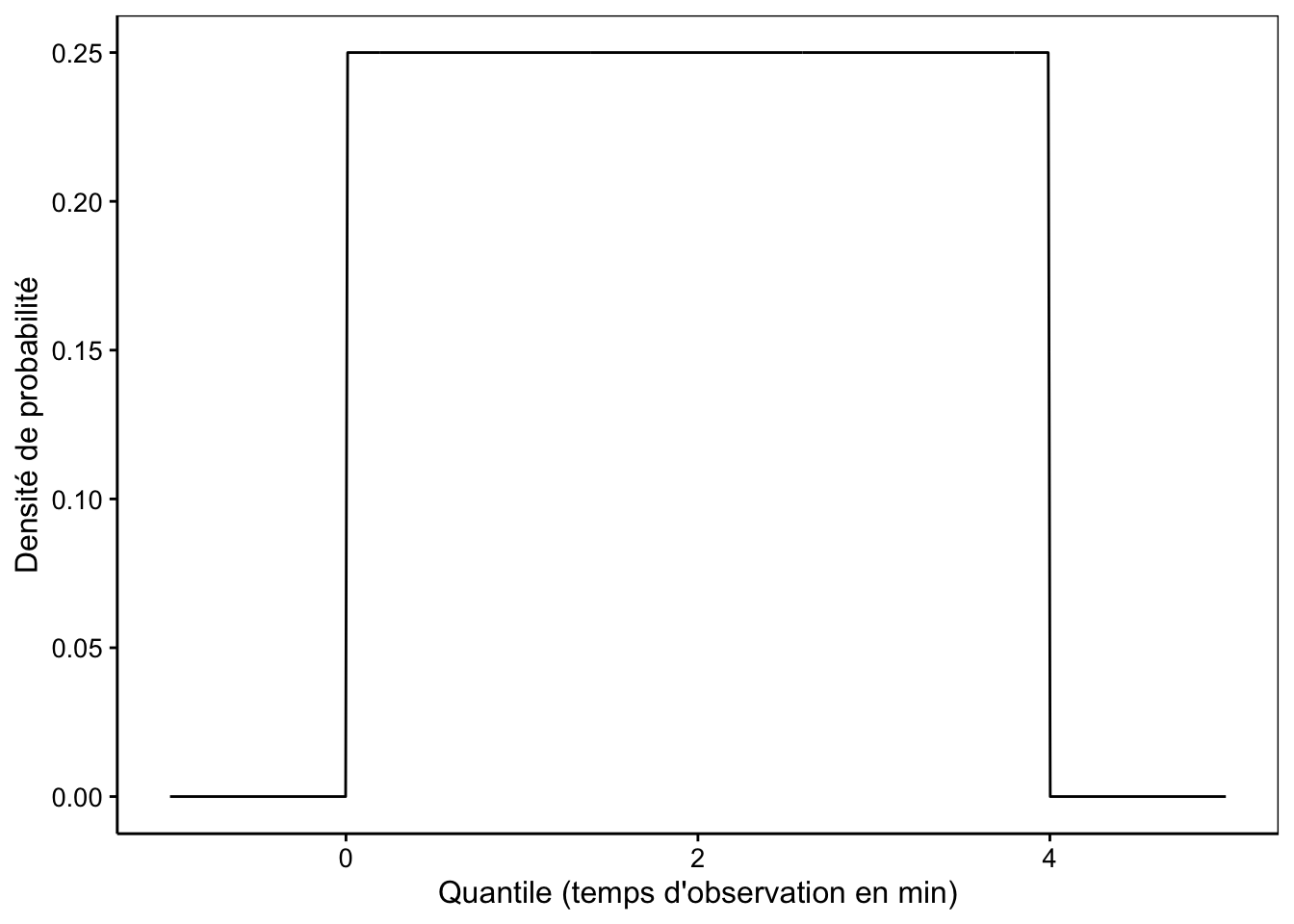
Figure 7.2: Probabilité qu’un nouvel insecte butineur arrive dans un intervalle de 0 à 4 min si, en moyenne, un insecte arrive toutes les 4 min.
Une autre représentation courante est la densité de probabilité cumulée qui représente la probabilité d’observer un quantile ou moins. Dans le cas présent, cela représente la probabilité qu’au moins un insecte butineur soit observé pour des durées d’observation croissantes (Fig. 7.3).
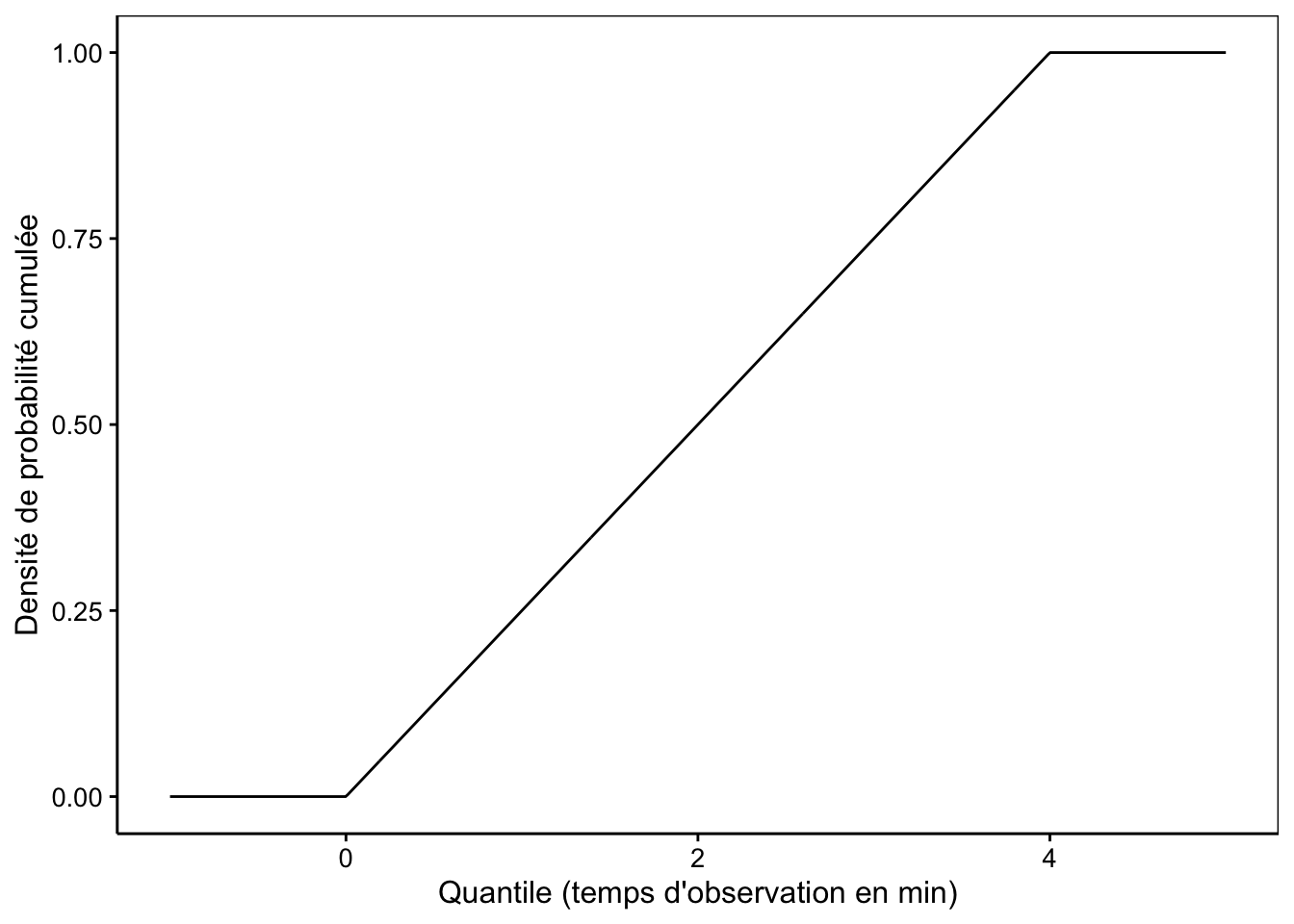
Figure 7.3: Probabilité cumulée qu’un nouvel insecte butineur arrive dans un intervalle de 0 à 4 min si, en moyenne, un insecte arrive toutes les 4 min.
Notation : nous noterons qu’une variable suit une loi de distribution comme ceci (le tilde ~ se lit “suit une distribution”, et U représente la distribution uniforme avec entre parenthèses, les paramètres de la distribution, ici, les bornes inférieure et supérieure de la distribution) :
\[X \sim U(0, 4)\]
Cela signifie : “la variable aléatoire X suit une distribution uniforme 0 à 4”.
La distribution \(U(0, 1)\) est particulière et est appelée distribution uniforme standard. Elle a la propriété particulière que si \(X \sim U(0, 1)\) alors \((1-X) \sim U(0, 1)\).
7.3.3 Quantiles vers probabilités
L’aire sous la courbe représente une probabilité associée à l’intervalle considéré pour les quantiles qui bornent l’aire calculée. Concrètement, quelle est la probabilité que X, le temps d’attente pour observer un insecte butineur, soit compris entre 2 et 2.5 min ? Nous pouvons répondre en calculant l’aire sous la courbe entre les quantiles 2 et 2.5 (représentée par l’aire en rouge à la Fig. 7.4).
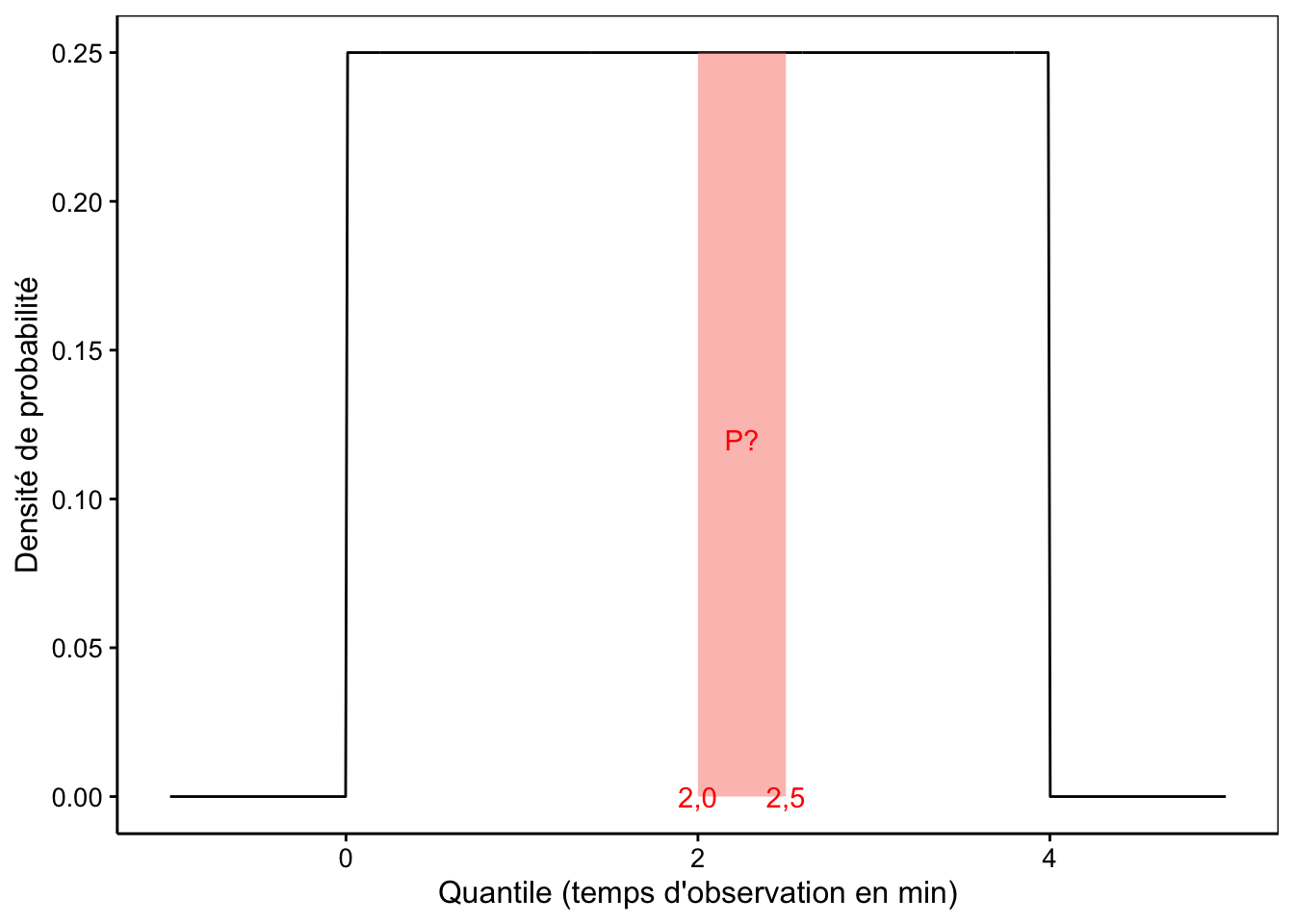
Figure 7.4: Probabilité qu’un insecte butineur arrive entre 2 et 2.5 min après le début d’une observation (aire en rouge).
Ici, le calcul est assez simple à faire à la main. Mais nous verrons d’autres lois de distribution plus complexes. Dans tous les cas, R offre des fonctions qui calculent les aires à gauche ou à droite d’un quantile donné. Le nom de la fonction est toujours p<distri>(), avec pour la distribution uniforme punif(). L’aire à gauche du quantile nécessite de spécifier l’argument lower.tail = TRUE (“queue en bas de la distribution” en anglais). Pour l’aire à droite, on indiquera évidemment lower.tail = FALSE. Donc, pour calculer la probabilité qu’un insecte arrive en moins de 2.5 minutes, nous écrirons :
# [1] 0.625À vous de jouer !
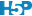
Mais comme nous voulons déterminer la probabilité qu’un insecte arrive entre 2 et 2.5 minutes, nous devons soustraire à cette valeur la probabilité qu’un insecte arrive en moins de 2 min (la zone en rouge dans la Fig 7.4 est en effet l’aire à gauche depuis le quantile 2.5 moins l’aire à gauche depuis le quantile 2) :
# [1] 0.125La réponse est 0.125, soit une fois sur huit observations, en moyenne, le temps d’attente enregistré sera compris entre 2 et 2.5 minutes.
Le calcul de probabilités sur base de lois de distributions continues se fait via les aires à gauche ou à droite d’un quantile sur le graphique de densité de probabilité. Pour une aire centrale, nous soustrayons les aires à gauche des deux quantiles respectifs.
7.3.4 Probabilités vers quantiles
Le calcul inverse est parfois nécessaire. Par exemple pour répondre à la question suivante :
- Combien de temps devons-nous patienter pour observer l’arrivée d’un insecte butineur sur la fleur une fois sur trois observations en moyenne ?
Ici, nous partons d’une probabilité (1/3) et voulons déterminer le quantile qui définit une aire à gauche de 1/3 sur le graphique (Fig. 7.5).
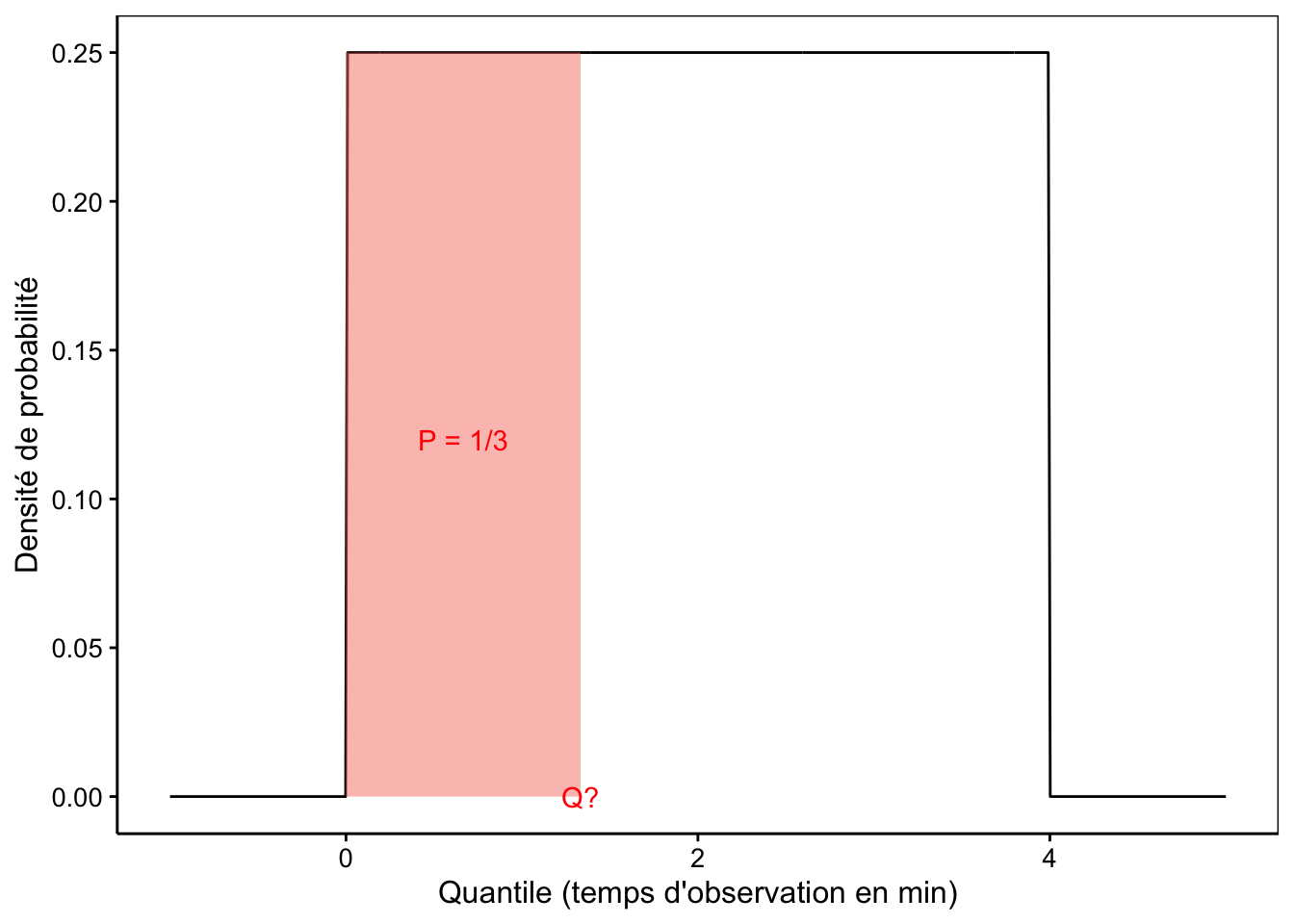
Figure 7.5: Temps d’observation nécessaire (quantile Q) pour voir arriver un butineur une fois sur trois (aire P en rouge de 1/3 à gauche de Q).
Dans R, la fonction qui effectue ce calcul est q<distri>(). Donc ici, il s’agit de qunif(). Les arguments sont les mêmes que pour punif() sauf le premier qui est une ou plusieurs probabilités. Nous répondons à la question de la façon suivante :
# [1] 1.333333Donc il faut observer pendant 1.33 min (1 min et 20 secs) pour avoir une chance sur trois d’observer l’arrivée d’un insecte butineur.
7.3.5 Calculs dans R
Dans R de base, pour chaque distribution statistique, quatre fonctions sont proposées qui commencent par p/q/r/d, suivi d’un diminutif pour la loi de distribution. Pour la distribution uniforme, c’est unif. Nous avons donc :
| fonction | rôle |
|---|---|
punif(q, min = 0, max = 1, lower.tail = TRUE, …) |
Calcule une ou plusieurs probabilités à partir de quantile(s) |
qunif(p, min = 0, max = 1, lower.tail = TRUE, …) |
Calcule un ou plusieurs quantiles à partir de probabilité(s) |
runif(n, min = 0, max = 1) |
Simule un échantillon de n nombres tirés au hasard de cette distribution (nombres pseudo-aléatoires) |
dunif(x, min = 0, max = 1, …) |
Calcule la densité de probabilité pour divers quantiles x |
Avec SciViews::R("infer"), nous avons aussi une autre façon de manipuler les distributions statistiques qui consiste à définir un objet distribution qui contient l’information relative à votre distribution, et à ensuite utiliser des méthodes pour en extraire une information ou pour effectuer des calculs dessus. Les fonctions qui créent les distributions commencent toutes par dist_. Pour la distribution uniforme, il s’agit de dist_uniform(min, max). Donc, nous créons la distribution uniforme pour nos insectes butineurs comme suit :
# <distribution[1]>
# [1] U(0, 4)À la place des variantes p/q/r/d, nous avons quatre méthodes que nous pouvons appliquer sur notre objet U :
cdf(U, q = ...)pour “cumulative distribution function” qui calcule l’aire à gauche d’un ou plusieurs quantiles, donc, l’équivalent depunif(q = ..., min = 0, max = 4, lower.tail = TRUE). Il n’y a pas de fonction pour calculer l’aire à droite, mais comme on sait que c’est le complément à un, on fera1 - cdf(U, q = ...).quantile(U, p = ...), équivalent dequnif(p = ..., min = 0, max = 4, lower.tail = TRUE).generate(U, times = ...)[[1]]équivalent derunif(n = ..., min = 0, max = 4).density(U, x = ...)[[1]]équivalent àdunif(x = ..., min = 0, max = 4).
# [1] 0.75# [1] 0.75# [1] 1.333333# [1] 1.333333# [1] 0.25 0.25 0.25# [1] 0.25 0.25 0.25# [1] 3.5515874 3.6412791 1.4006474 0.2001286 3.8390097# [1] 3.5515874 3.6412791 1.4006474 0.2001286 3.8390097Notez l’utilisation de set.seed() ici. Cette fonction initialise le générateur de nombres pseudo-aléatoires. Il s’agit d’un code informatique qui génère une suite de nombres qui a des propriétés équivalentes à une série réellement aléatoire, mais sans l’être réellement. On initie le générateur à un endroit dans la suite de nombres à l’aide de set.seed() auquel on donne un nombre entier au hasard comme argument (naturellement, on doit donner à chaque fois un autre nombre, … sauf si on veut générer exactement la même suite, comme c’est le cas ci-dessus pour comparer la sortie de generate(U) par rapport à runif()). L’utilisation de set.seed() rend votre code reproductible. N’hésitez donc pas à l’utiliser avant tout calcul faisant intervenir le générateur de nombres pseudo-aléatoires dans vos documents comme ceci :
# [1] 0.6378020 0.7524999 0.5593599 0.6688387 0.8989262 0.5300384 0.1520689
# [8] 0.9031163 0.2693327 0.6738862À vous de jouer !
Mais revenons à notre comparaison des fonctions p/q/r/d et des méthodes de l’objet distribution. Un premier avantage que vous aurez certainement remarqué, c’est que les paramètres de la distribution (ici min = et max =) ne sont introduits qu’une seule fois, à la construction de notre objet U. Si la distribution doit être utilisée plusieurs fois, c’est un avantage. Ensuite, nous pouvons aussi avoir d’autres informations relatives à cette distribution, par exemple (voyez l’aide en ligne de ces différentes fonctions pour plus de détails) :
# [1] "U(0, 4)"# # A data.frame: 1 x 2
# l u
# <dbl> <dbl>
# 1 0 4# [1] 2# [1] 1.333333# <support_region[1]>
# [1] [0,4]Bien que nous ne l’utiliserons pas dans ce cours, les objets distribution peuvent contenir plusieurs distributions différentes, et même, une mixture de plusieurs distributions. Enfin, dernier avantage, à condition de charger le package BioDataScience1 à l’aide de l’instruction library(BioDataScience1), vous pouvez utiliser chart() pour créer le graphique de densité de probabilité ou chart$cumulative() pour tracer le graphique de densité de probabilité cumulée très facilement pour distribution. Ensuite, vous y ajouter une aire à l’aide de geom_funfill() en utilisant dfun() pour une aire de densité ou cdfun() pour une aire de densité cumulée. Pour annoter le graphique, vous utilisez annotate("text"). Voici ce que cela donne :
chart(U) +
geom_funfill(fun = dfun(U), from = 1, to = 3) +
annotate("text", x = 2, y = 0.10, label = "P[1, 3]", col = "red")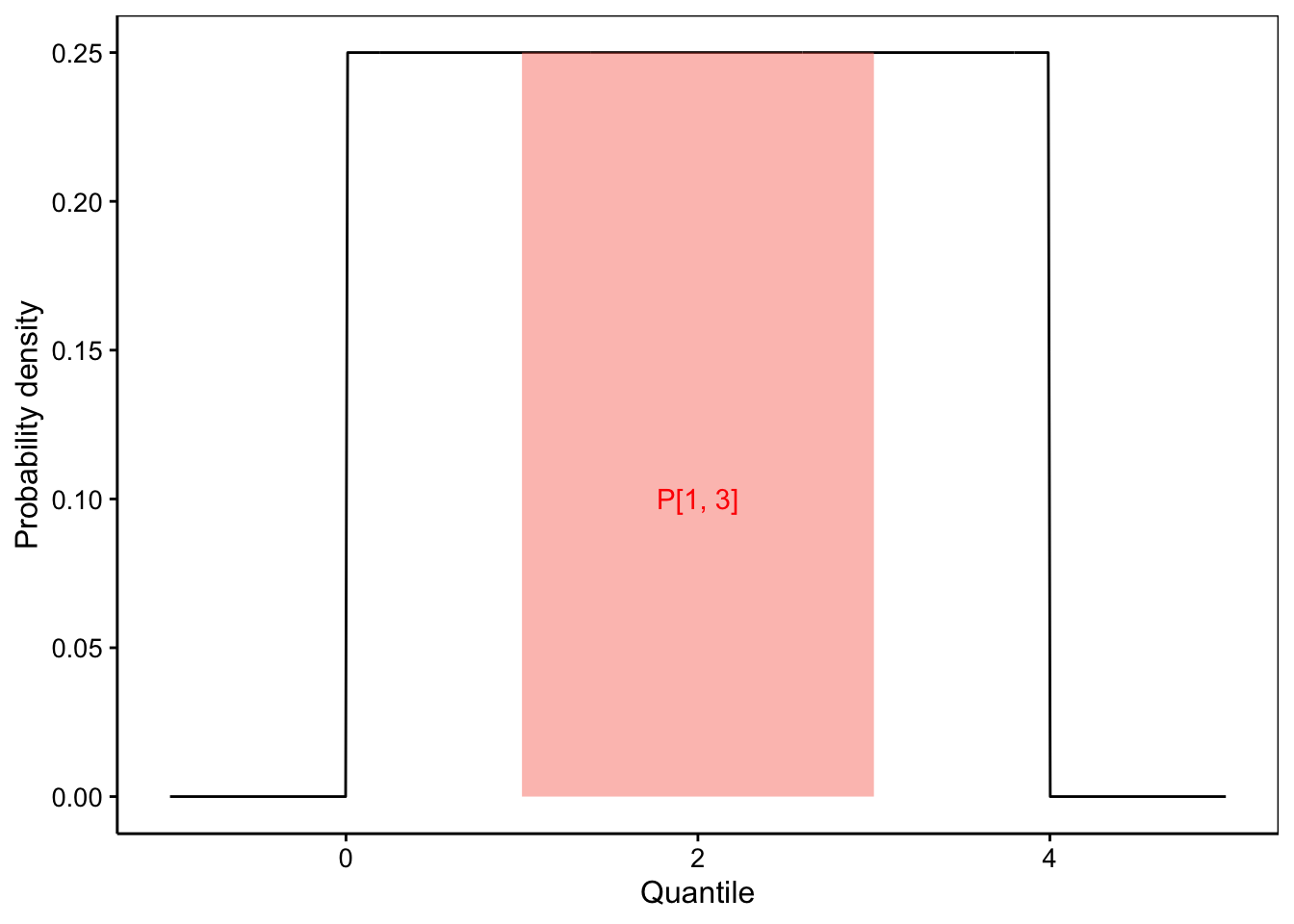
… et pour le graphique de densité de probabilité cumulée :
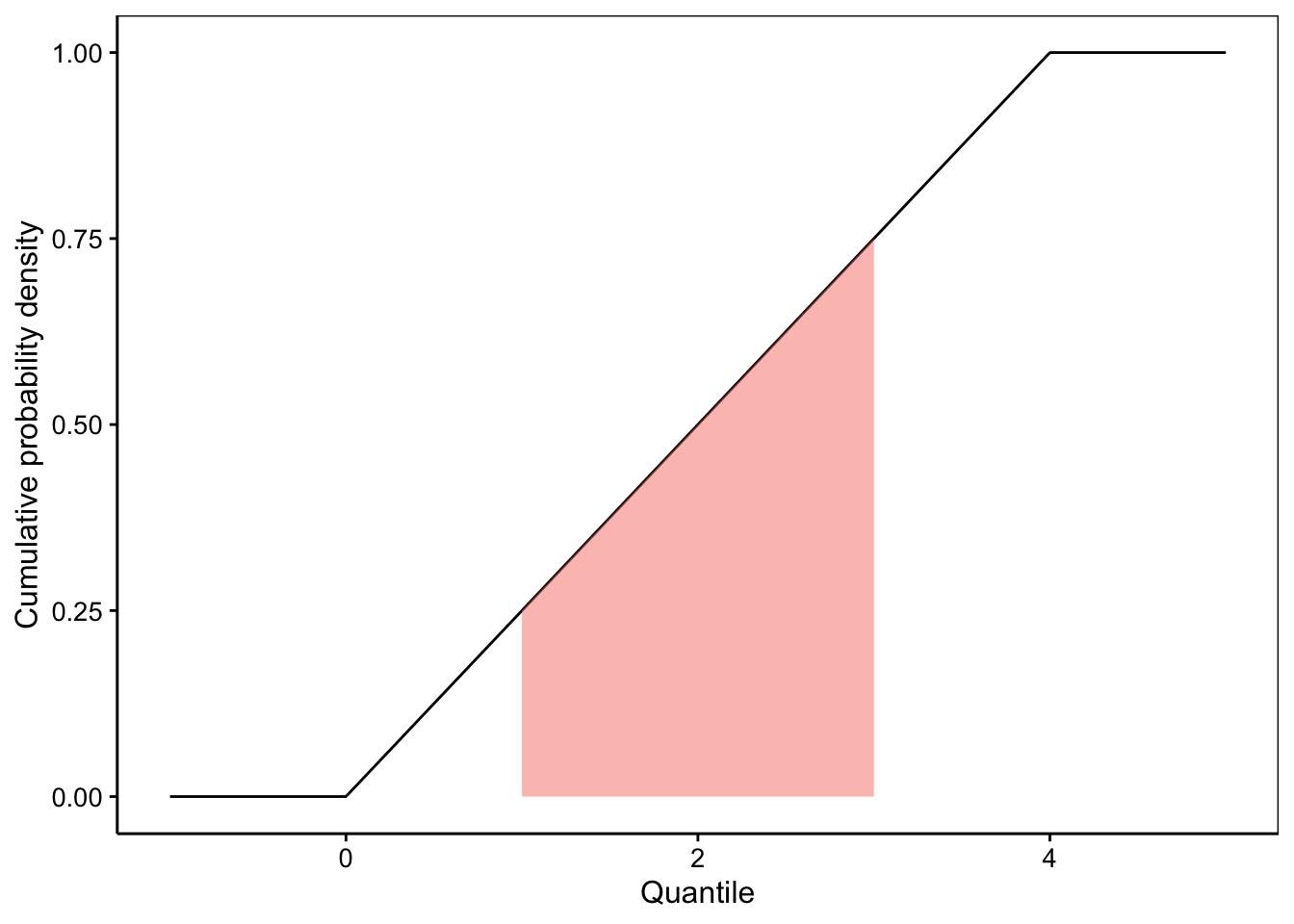
Plus la densité de probabilité est élevée, plus les évènements dans cette région du graphique sont probables.↩︎