11.4 Facteurs hiérarchisés

Nous n’avons pas toujours la possibilité de croiser les deux facteurs. Considérons le cas d’une étude d’intercalibration. Nous avons un ou plusieurs échantillons répartis entre plusieurs laboratoires, et comme les analyses dépendent éventuellement aussi du technicien qui fait la mesure, nous demandons à chaque laboratoire de répéter les mesures avec deux de leurs techniciens. Problème : ici, il s’agit bien évidemment de techniciens différents dans chaque laboratoire. Comment faire, sachant que pour le modèle croisé, il faudrait que les deux mêmes techniciens aient fait toutes les mesures dans tous les laboratoires ?

La solution est le modèle à facteurs hiérarchisés qui s’écrit :

\[y_{ijk} = \mu + \tau1_j + \tau2_k(\tau1_j) + \epsilon_i \mathrm{\ avec\ } \ \epsilon_i \sim N(0, \sigma) \]

… et dans R, nous utiliserons la formule suivante :

\[y \sim fact1 + fact2\ \%in\%\ fact1\]

Voici un exemple concret. Un gros échantillon homogène d’œufs déshydratés est réparti entre six laboratoires différents en vue de la détermination de la teneur en matières grasses dans cet échantillon. Le but de la manœuvre est de déterminer si les laboratoires donnent des résultats consistants entre eux. Les deux techniciens de chaque laboratoire sont libellés one et two, mais ce sont en fait à chaque fois des techniciens différents dans chaque laboratoire49.

eggs <- read("eggs", package = "faraway")
skimr::skim(eggs)
Tableau 11.1: Data summary
Name eggs
Number of rows 48
Number of columns 4
Key NULL
_______________________
Column type frequency:
factor 3
numeric 1
________________________
Group variables None

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
Lab 0 1 FALSE 6 I: 8, II: 8, III: 8, IV: 8
Technician 0 1 FALSE 2 one: 24, two: 24
Sample 0 1 FALSE 2 G: 24, H: 24

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
Fat 0 1 0.39 0.15 0.06 0.31 0.37 0.43 0.8 ▂▅▇▂▁

Commençons par corriger l’encodage erroné des techniciens qui ferait penser que seulement deux personnes ont travaillé dans l’ensemble des six laboratoires.

eggs <- fmutate(eggs, Technician = interaction(Lab, Technician))
skimr::skim(eggs)
Tableau 11.2: Data summary
Name eggs
Number of rows 48
Number of columns 4
Key NULL
_______________________
Column type frequency:
factor 3
numeric 1
________________________
Group variables None

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
Lab 0 1 FALSE 6 I: 8, II: 8, III: 8, IV: 8
Technician 0 1 FALSE 12 I.o: 4, II.: 4, III: 4, IV.: 4
Sample 0 1 FALSE 2 G: 24, H: 24

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
Fat 0 1 0.39 0.15 0.06 0.31 0.37 0.43 0.8 ▂▅▇▂▁

Nous avons à présent douze techniciens notés I.one, I.two, II.one, II.two, … Nous pouvons visualiser ces données. Comme nous n’avons que quatre réplicas par technicien, nous nous limitons à la représentation des observations de départ et des moyennes.

chart(data = eggs, Fat ~ Lab %col=% Technician) +
  geom_jitter(width = 0.05, alpha = 0.5) +
  stat_summary(geom = "point", fun = "mean", color = "red", size = 3)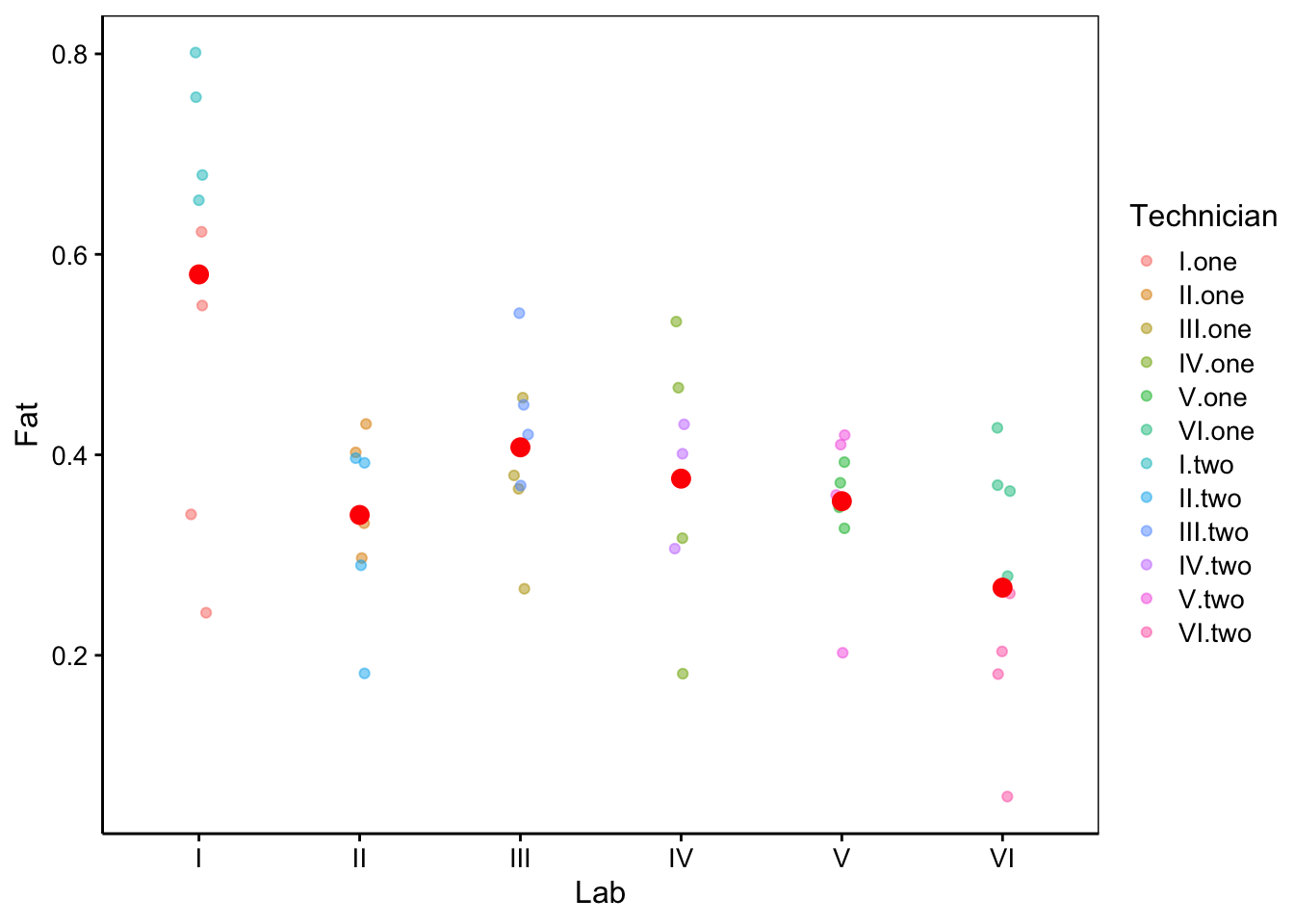
Mesures de fractions en matières grasses dans des oeufs dans six laboratoires, par douze techniciens différents. Les points rouges sont les moyennes par technicien.

Figure 11.5: Mesures de fractions en matières grasses dans des oeufs dans six laboratoires, par douze techniciens différents. Les points rouges sont les moyennes par technicien.

Vérifions l’homoscédasticité. Ici, il suffit de considérer la variable Technician (une fois correctement encodée !) parce que dans cette forme de modèle, le facteur qui est imbriqué (Technician) est celui à partir duquel les résidus sont calculés. Nous utiliserons un seuil \(\alpha\) classique de 5% pour l’ensemble de nos tests dans cette étude.

bartlett.test(data = eggs, Fat ~ Technician)
# 
#   Bartlett test of homogeneity of variances
# 
# data:  Fat by Technician
# Bartlett's K-squared = 13.891, df = 11, p-value = 0.2391

Avec une valeur p de 23,9%, nous pouvons considérer qu’il y a homoscédasticité. Voilà l’ANOVA réalisée en utilisant la formule pour le modèle hiérarchisé (on dit aussi modèle imbriqué) :

anova(eggs_anova <- lm(data = eggs, Fat ~ Lab + Technician %in% Lab))
# Analysis of Variance Table
# 
# Response: Fat
#                Df  Sum Sq  Mean Sq F value    Pr(>F)    
# Lab             5 0.44303 0.088605  9.5904 6.989e-06 ***
# Lab:Technician  6 0.24747 0.041246  4.4644  0.001786 ** 
# Residuals      36 0.33260 0.009239                      
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Nous voyons que, dans le cas présent, l’effet technicien ne peut pas être testé. Nous avons l’effet labo à la première ligne et les interactions entre les techniciens et les laboratoires qui sont présentés à la seconde ligne (et les résidus en dernière ligne comme d’habitude). Les deux tests (Lab et Lab:Technician) sont significatifs ici puisque les valeurs p sont toutes les deux inférieures à notre seuil \(\alpha\). fixé d’avance à 5%. Nous avons à la fois des différences significatives qui apparaissent entre laboratoires, mais aussi, des variation d’un labo à l’autre entre techniciens (interactions).

Nous devons maintenant vérifier la distribution Normale des résidus dans ce modèle (Fig. 11.6). Ici la distribution des résidus est acceptable, toujours considérant que l’ANOVA est relativement robuste vis à vis de petits écarts. Dans la partie basse de la distribution, on est bon (un ou deux points un peu éloignés sont relativement habituels sur ce genre de graphique). En partie haute, nous avons un écart qui se marque, mais pas de manière dramatique.

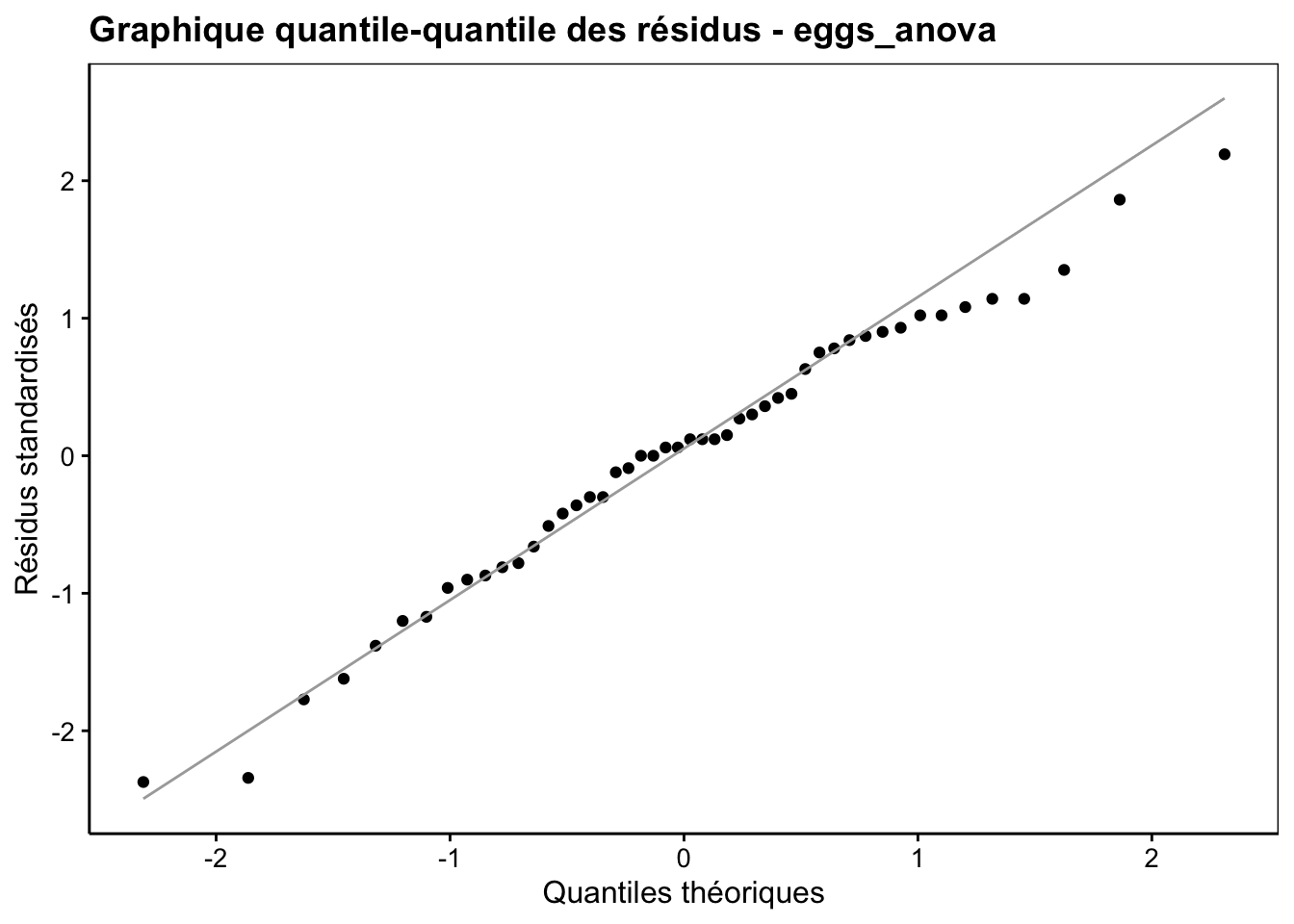
Graphique quantile-quantile des résidus de l'ANOVA à deux facteurs hiérarchisés pour la variable `Fat` du jeu de données `eggs`.

Figure 11.6: Graphique quantile-quantile des résidus de l’ANOVA à deux facteurs hiérarchisés pour la variable Fat du jeu de données eggs.

L’effet qui nous intéresse en priorité est l’effet laboratoire. Effectuons des tests “post hoc” sur cet effet pour déterminer quel(s) laboratoire(s) diffèrent entre eux. Le code que nous utilisons habituellement ne fonctionne pas dans le cas d’un modèle hiérarchisé, mais nous pouvons utiliser la fonction TukeyHSD() à la place, en partant d’un modèle similaire créé à l’aide de la fonction aov().

eggs_aov <- aov(data = eggs, Fat ~ Lab + Technician %in% Lab)
(eggs_posthoc <- TukeyHSD(eggs_aov, "Lab"))
#   Tukey multiple comparisons of means
#     95% family-wise confidence level
# 
# Fit: aov(formula = Fat ~ Lab + Technician %in% Lab, data = eggs)
# 
# $Lab
#            diff         lwr          upr     p adj
# II-I   -0.24000 -0.38459081 -0.095409195 0.0002088
# III-I  -0.17250 -0.31709081 -0.027909195 0.0116356
# IV-I   -0.20375 -0.34834081 -0.059159195 0.0019225
# V-I    -0.22625 -0.37084081 -0.081659195 0.0004902
# VI-I   -0.31250 -0.45709081 -0.167909195 0.0000021
# III-II  0.06750 -0.07709081  0.212090805 0.7240821
# IV-II   0.03625 -0.10834081  0.180840805 0.9733269
# V-II    0.01375 -0.13084081  0.158340805 0.9997181
# VI-II  -0.07250 -0.21709081  0.072090805 0.6611505
# IV-III -0.03125 -0.17584081  0.113340805 0.9861403
# V-III  -0.05375 -0.19834081  0.090840805 0.8705387
# VI-III -0.14000 -0.28459081  0.004590805 0.0624025
# V-IV   -0.02250 -0.16709081  0.122090805 0.9969635
# VI-IV  -0.10875 -0.25334081  0.035840805 0.2356038
# VI-V   -0.08625 -0.23084081  0.058340805 0.4817411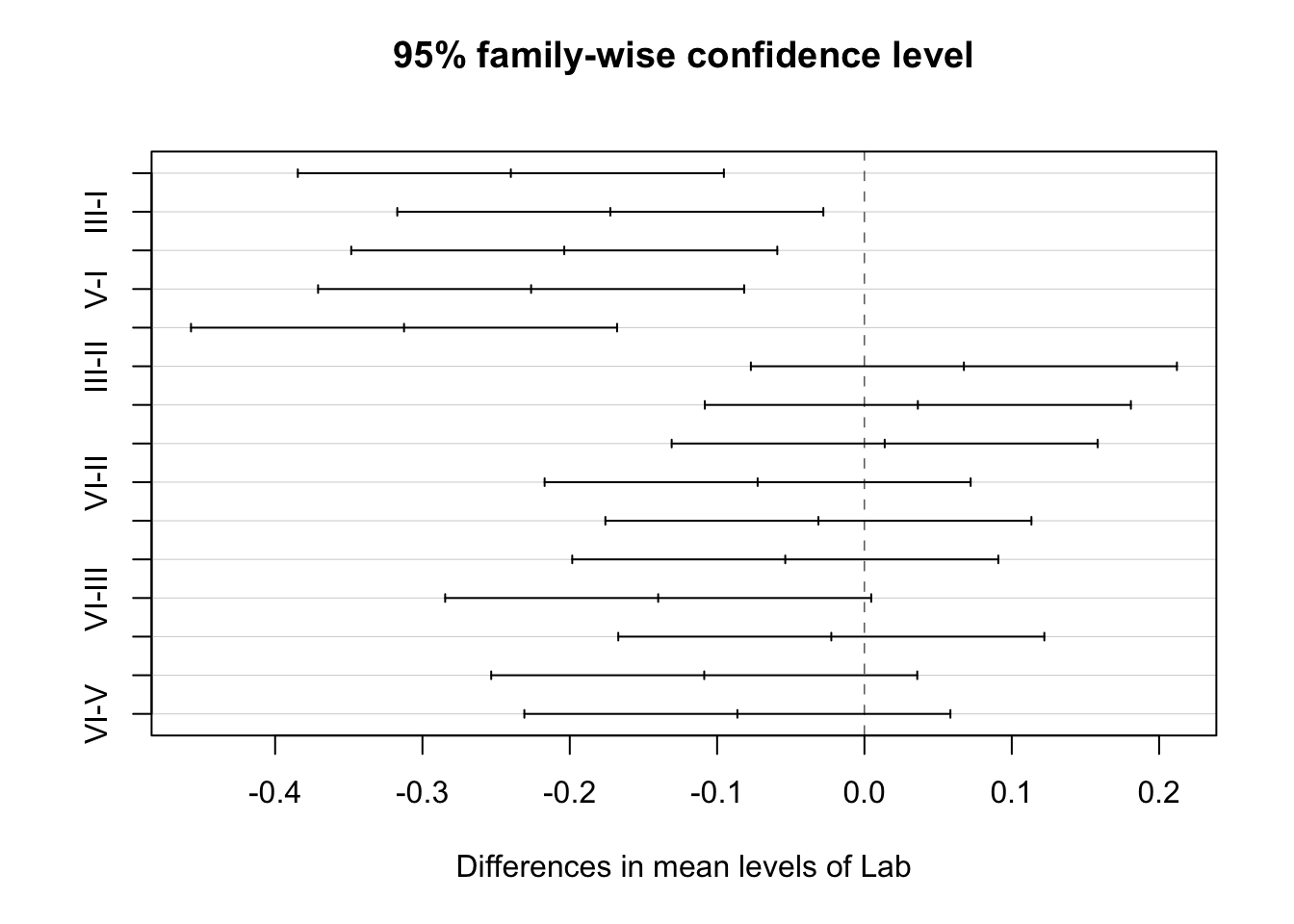
plot(eggs_posthoc)

Nous pouvons observer des différences significatives au seuil \(\alpha\) de 5% entre le labo I et tous les autres laboratoires. Les autres comparaisons n’apparaissent pas significatives, toujours au seuil de 5%.

11.4.1 Simplification du modèle

Nous pourrions être tentés de simplifier notre analyse en ne testant que l’effet laboratoire. Dans ce cas, nous tomberions dans le piège de la pseudo-réplication. Nous pourrions aussi travailler sur la mesure moyenne des mesures pour chaque technicien. Du coup, nous aurions deux valeurs par laboratoire, chaque fois réalisée par un technicien différent. Nous pourrions donc considérer que les données sont indépendantes les unes des autres et nous pourrions réduite le problème à un effet unique, celui du laboratoire.

Si nous n’avons plus que deux mesures par laboratoire au lieu de deux fois quatre, nous gagnons d’un autre côté puisque l’écart type de la moyenne d’un échantillon et l’écart type de la population divisé par la racine carré de n. Donc, l’écart type sur les mesures moyennes est alors deux fois plus faible, ce qui se répercutera de manière positive sur l’ANOVA. La distribution des résidus sera une distribution t de Student, mais elle est symétrique et pas trop différente d’une distribution Normale. Cela pourrait passer. Mais il se peut que la réduction de l’information soit telle que le test perde complètement sa puissance. Illustrons ce phénomène avec le jeu de données eggs. Nous créons le jeu de données eggs_means reprenant les moyennes des quatre mesures par technicien dans la variable Fat_mean.

eggs %>.%
  sgroup_by(., Technician) %>.%
  ssummarise(.,
    Fat_mean = fmean(Fat),
    Lab      = funique(Lab)) %->%
  eggs_means
skimr::skim(eggs_means)
Tableau 11.3: Data summary
Name eggs_means
Number of rows 12
Number of columns 3
Key NULL
_______________________
Column type frequency:
factor 2
numeric 1
________________________
Group variables None

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
Technician 0 1 FALSE 12 I.o: 1, II.: 1, III: 1, IV.: 1
Lab 0 1 FALSE 6 I: 2, II: 2, III: 2, IV: 2

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
Fat_mean 0 1 0.39 0.13 0.17 0.36 0.37 0.39 0.72 ▁▇▂▁▁ 
eggs_means %>.%
  sgroup_by(., Lab) %>.%
  ssummarise(.,
    mean  = fmean(Fat_mean),
    sd    = fsd(Fat_mean),
    count = fnobs(Fat_mean))
# # A data.table: 6 x 4
# # Language:     fr
#   Lab    mean      sd count
#   <fct> <dbl>   <dbl> <int>
# 1 I     0.58  0.202       2
# 2 II    0.34  0.0354      2
# 3 III   0.408 0.0530      2
# 4 IV    0.376 0.00177     2
# 5 V     0.354 0.00884     2
# 6 VI    0.267 0.131       2

Représentation graphique et vérification de l’homoscédasticité.

chart(eggs_means, Fat_mean ~ Lab) +
  geom_point() +
  stat_summary(geom = "point", fun = "mean", color = "red", size = 3)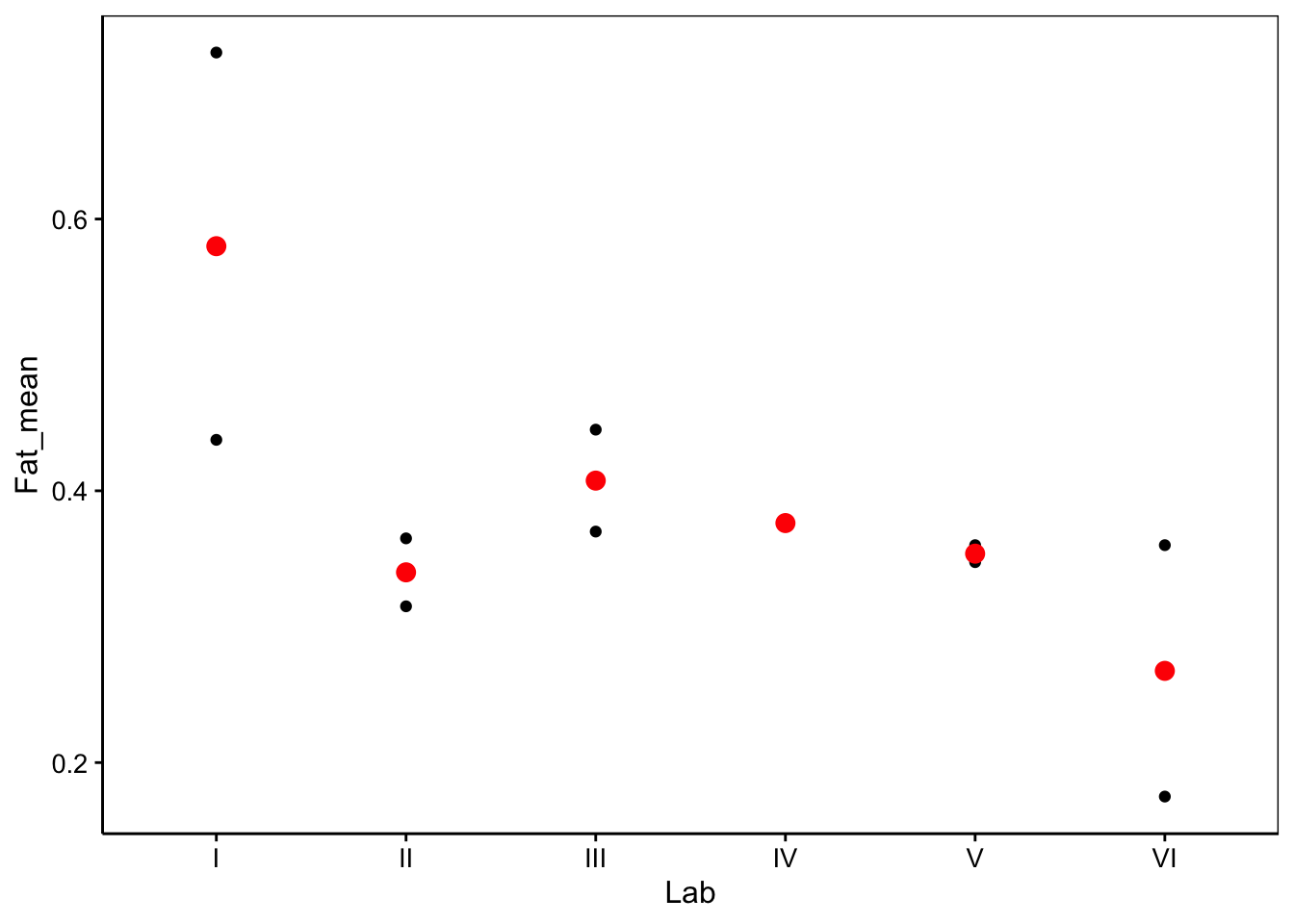

bartlett.test(data = eggs_means, Fat_mean ~ Lab)
# 
#   Bartlett test of homogeneity of variances
# 
# data:  Fat_mean by Lab
# Bartlett's K-squared = 10.452, df = 5, p-value = 0.0634

Notez ceci : le test de Bartlett nous donne une valeur p de 6%, donc supérieure au seuil \(\alpha\) de 5%. Nous serons donc tenté de considérer qu’il y a homoscédasticité (no rejet de H0)… mais avec un regard plus critique, nous gardons à l’esprit que deux mesures par laboratoire, c’est vraiment pas beaucouo. Le graphique tend à nous montrer que les écarts entre les deux mesures peuvent varier quand même énormément d’un laboratoire à l’autre. Ici, il faudrait une étude avec plus de mesures pour réellement conclure sur ce test ! Nous pouvons quand même effecter notre analyse de variance à un facteur.

anova(eggs_means_anova <- lm(data = eggs_means, Fat_mean ~ Lab))
# Analysis of Variance Table
# 
# Response: Fat_mean
#           Df   Sum Sq  Mean Sq F value Pr(>F)
# Lab        5 0.110756 0.022151  2.1482 0.1895
# Residuals  6 0.061869 0.010311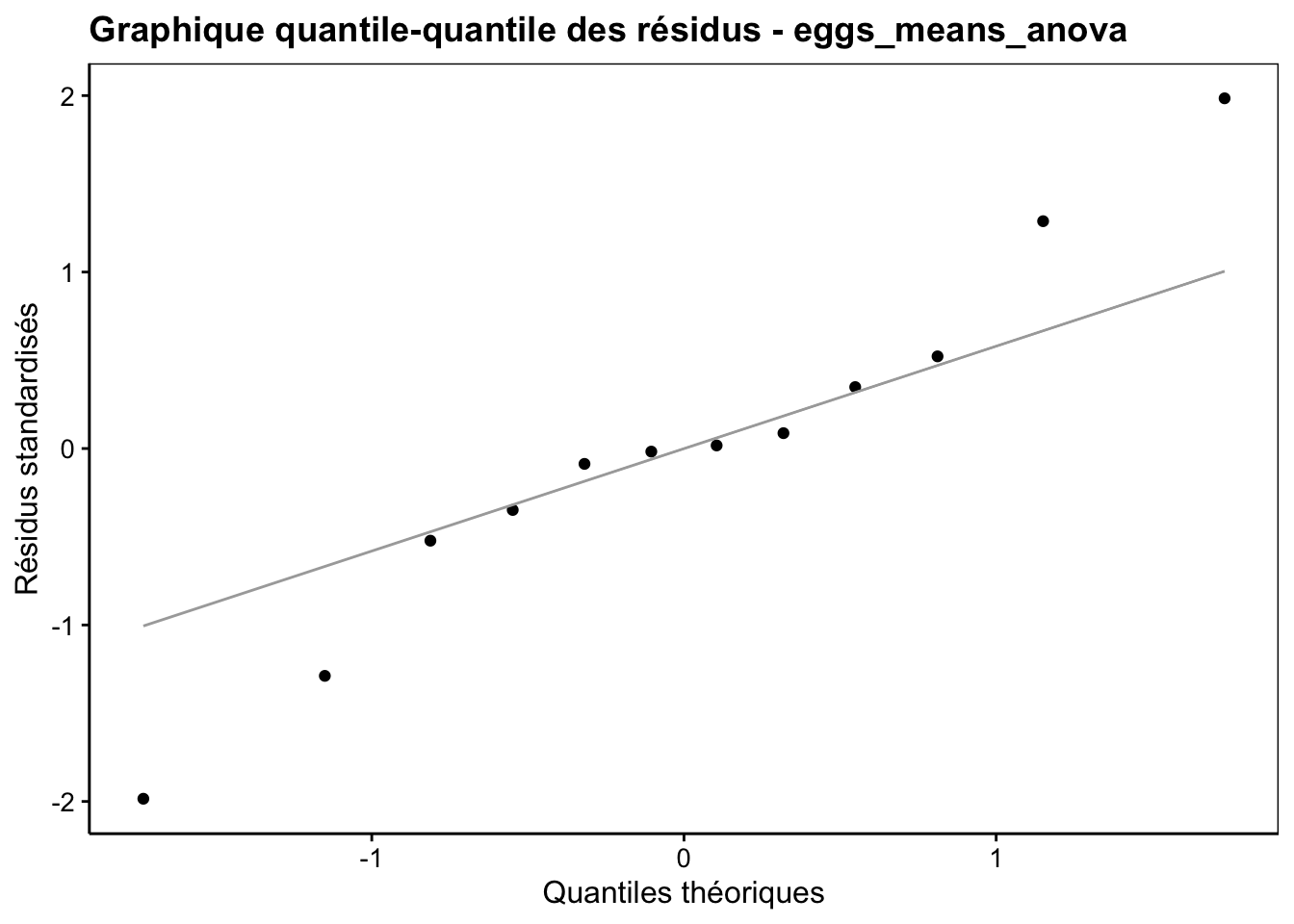
chart$qqplot(eggs_means_anova)

Nous n’avons plus d’effet significatif, malgré que le labo I obtient, en moyenne, une mesure beaucoup plus forte que les autres. En fait, en réduisant de la sorte nos données, nous avons perdu tellement d’information que le test a perdu toute puissance et n’est plus capable de détecter de manière significative des différences entre moyennes pourtant importantes. Idem pour l’hétéroscédasticité, et le graphique quantile-quantile ne parle pas non plus en la faveur de l’analyse.

Si nous avions quatre techniciens par labo qui avaient tous dosés les échantillons deux fois (également huit mesures par laboratoire au total), nous n’aurions pas une perte d’information aussi forte en effectuant quatre moyennes par laboratoire, et l’analyse simplifiée aurait peut-être été utilisable. Il faut voir au cas par cas… Quoi qu’il en soit, le modèle hiérarchisé montre ici qu’il est une alternative intéressant à la ANOVA à un facteur sur les données simplifiées.

Conditions d’application

Les conditions d’application sont les mêmes que pour l’ANOVA à deux facteurs sans interactions, sauf qu’ici, les interactions sont bien évidemment incluses dans le modèle par construction.

  1. La variable Sample valant G ou H ne sera pas utilisée ici. En fait, au départ, les initiateurs de l’expérience ont fait croire aux laboratoires qu’il s’agissait de deux échantillons différents alors que c’est le même en réalité.↩︎