3.2 Graphique de densité

L’histogramme n’est pas le seul outil à votre disposition. Vous pouvez également utiliser le graphique de densité qui se présente un peu comme un histogramme lissé. Le passage d’un histogramme vers un graphe de densité se base sur une estimation par noyau gaussien⁹

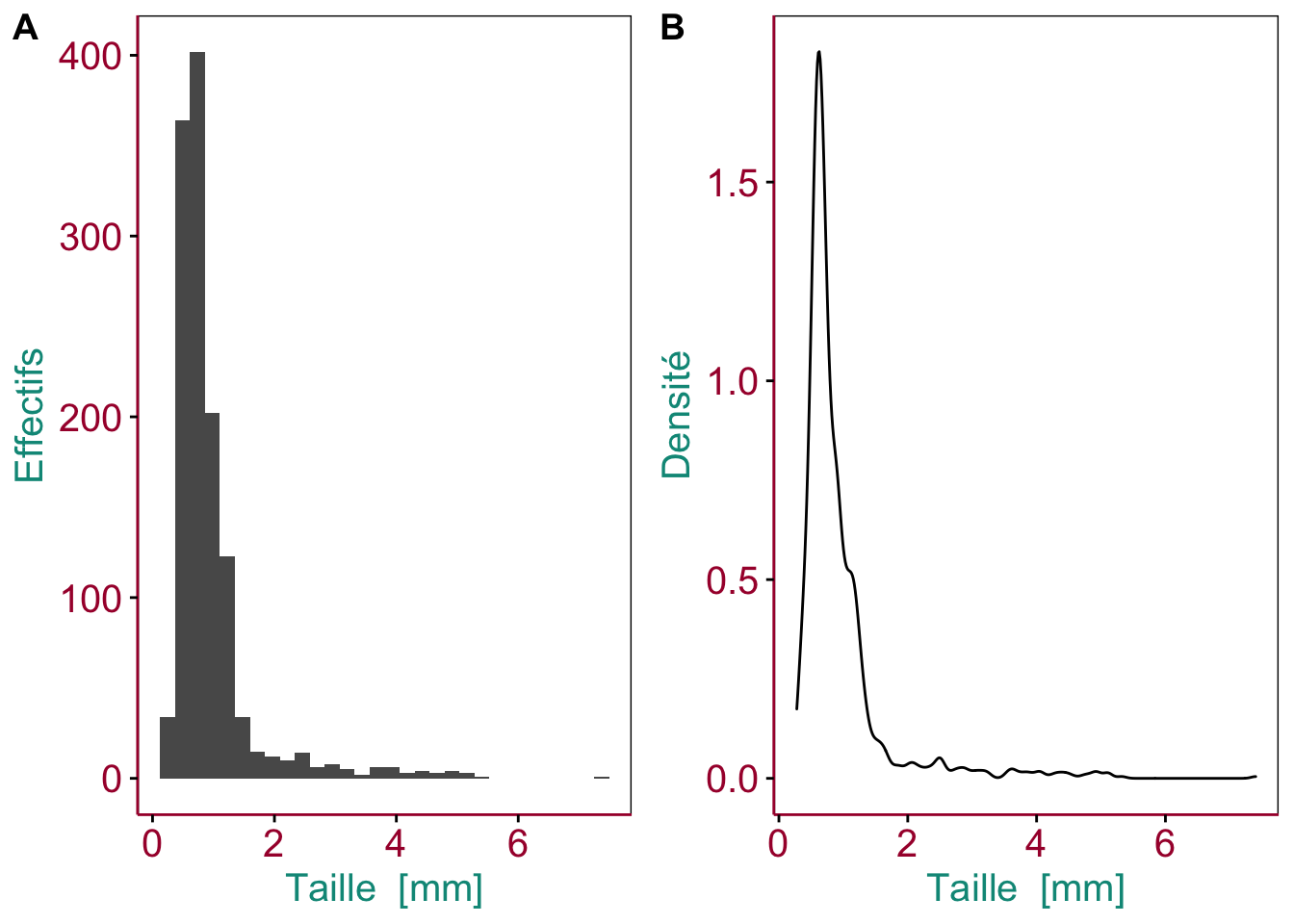
Figure 3.7: A. Histogramme et B. graphique de densité montrant la distribution de la taille de zooplancton étudié par analyse d’image. Les couleurs pour les axes et les labels servent à les mettre en évidence, mais en pratique ils seront noirs.

Comme pour les autres graphiques, veillez à soigner les indications qui permettent d’interpréter le graphique. Outre la courbe de densité, il faut :

• Les axes avec les graduations (en rouge)
• les labels des axes, et les unités pour l’axe des abscisses (en bleu)

Les instructions en R pour produire un graphique de densité avec la fonction chart() sont :

# Importation du jeu de données
(zooplankton <- read("zooplankton", package = "data.io", lang = "FR"))

# # A data.table: 1262 x 20
# # Language:     FR
#      ecd  area perimeter feret major minor  mean  mode   min   max std_dev range
#    <dbl> <dbl>     <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>   <dbl> <dbl>
#  1 0.770 0.465      4.45 1.32  1.16  0.509 0.363 0.036 0.004 0.908   0.231 0.904
#  2 0.700 0.385      2.32 0.728 0.713 0.688 0.361 0.492 0.024 0.676   0.183 0.652
#  3 0.815 0.521      4.15 1.33  1.11  0.598 0.308 0.032 0.008 0.696   0.204 0.688
#  4 0.785 0.484      4.44 1.78  1.56  0.394 0.332 0.036 0.004 0.728   0.218 0.724
#  5 0.361 0.103      1.71 0.739 0.694 0.188 0.153 0.016 0.008 0.452   0.110 0.444
#  6 0.832 0.544      5.27 1.66  1.36  0.511 0.371 0.02  0.004 0.844   0.268 0.84 
#  7 1.23  1.20      15.7  3.92  1.37  1.11  0.217 0.012 0.004 0.784   0.214 0.78 
#  8 0.620 0.302      3.98 1.19  1.04  0.370 0.316 0.012 0.004 0.756   0.246 0.752
#  9 1.19  1.12      15.3  3.85  1.34  1.06  0.176 0.012 0.004 0.728   0.172 0.724
# 10 1.04  0.856      7.60 1.89  1.66  0.656 0.404 0.044 0.004 0.88    0.264 0.876
# # … with 1,252 more rows, and 8 more variables: size <dbl>, aspect <dbl>,
# #   elongation <dbl>, compactness <dbl>, transparency <dbl>, circularity <dbl>,
# #   density <dbl>, class <fct>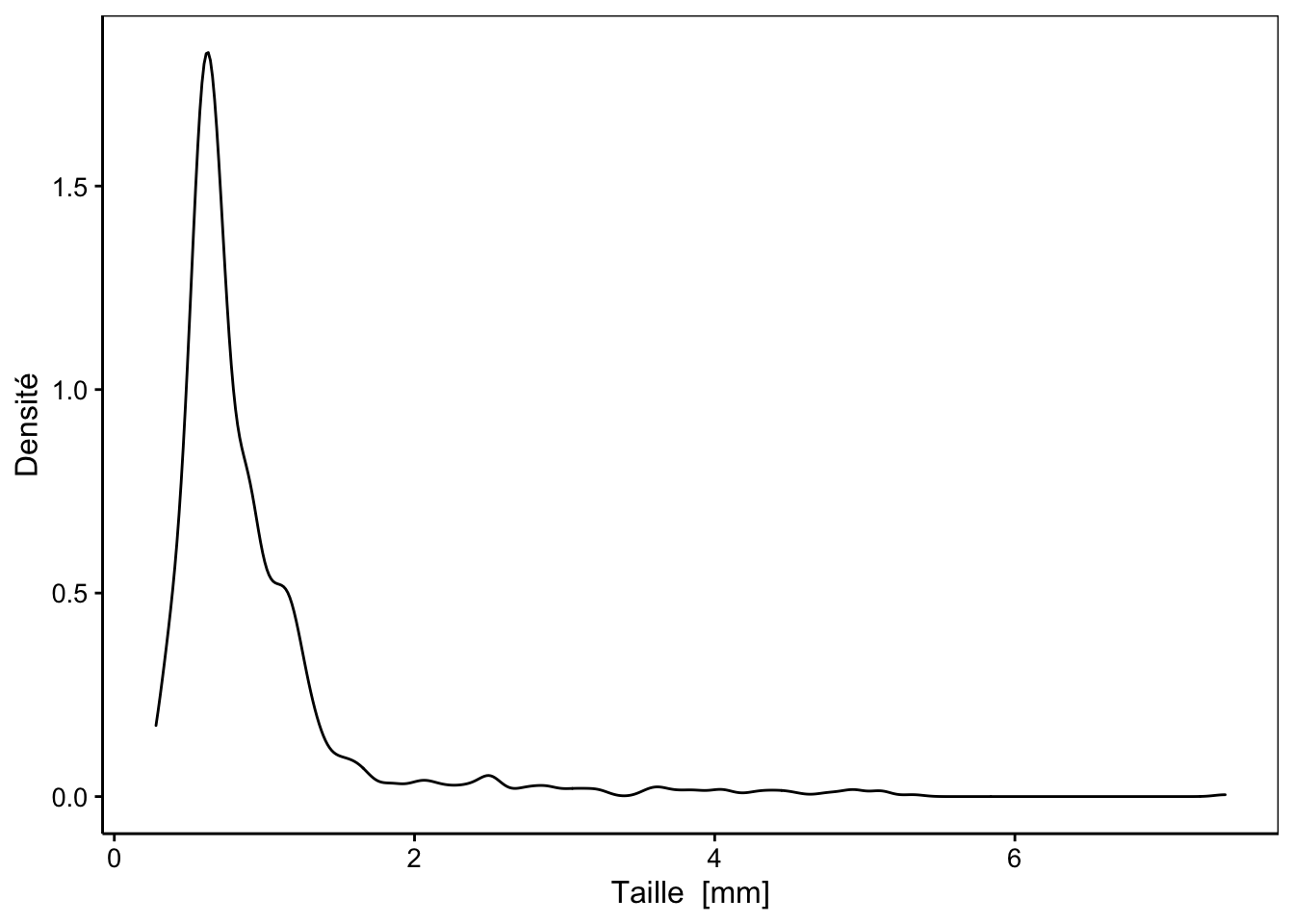

# Réalisation du graphique
chart(data = zooplankton, ~ size) +
  geom_density() +
  ylab("Densité")

Figure 3.8: Distribution des tailles au sein de l’échantillon de zooplancton.

Ici, nous utilisons donc la fonction geom_density().

À vous de jouer !

Réalisez le travail A03Ia_distributions.

Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques I : visualisation à l’UMONS à terminer avant le 2022-10-31 16:00:00.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md.

---

9. L’opération effectuée pour passer d’un histogramme à une courbe de densité consiste effectivement à lisser les pics plus ou moins fortement dans l’histogramme de départ.↩︎