7.3 Variables circulaires

Les variables circulaires se rencontrent de temps en temps en biologie. Lorsque c’est le cas, il est crucial de les reconnaître et de les traiter correctement. Imaginez que vous travaillez sur l’écophysiologie de végétaux. Les conditions météorologiques sont importantes à leur croissance : température, humidité, force et direction du vent. Prenons cette dernière variable, direction du vent. Elle peut s’exprimer en degrés de 0 à 360°, 0° correspondant au vent du nord et 180° au vent du sud. Vous enregistrez les données suivantes sur huit jours consécutifs pour la direction du vent en degrés :

meteo <- dtx(
  day      = 1:8,
  wind_dir = c(5, 15, 345, 350, 35, 355, 340, 20)
)
meteo
#      day wind_dir
#    <int>    <num>
# 1:     1        5
# 2:     2       15
# 3:     3      345
# 4:     4      350
# 5:     5       35
# 6:     6      355
# 7:     7      340
# 8:     8       20

Une des premières choses que nous pourrions faire est de calculer la moyenne et l’écart type de ces données :

mean(meteo$wind_dir)
# [1] 183.125
sd(meteo$wind_dir)
# [1] 175.9654

Nous en concluons donc qu’en moyenne, le vent est orienté au sud (presque 180°) et est extrêmement variable, car l’écart type est de presque 180° également… Vous voyez peut-être déjà le hic ici, sinon représentons graphiquement ces données. Un graphique naïf donne ceci, par exemple :

chart(data = meteo, wind_dir ~ day) +
  geom_point() +
  geom_line()

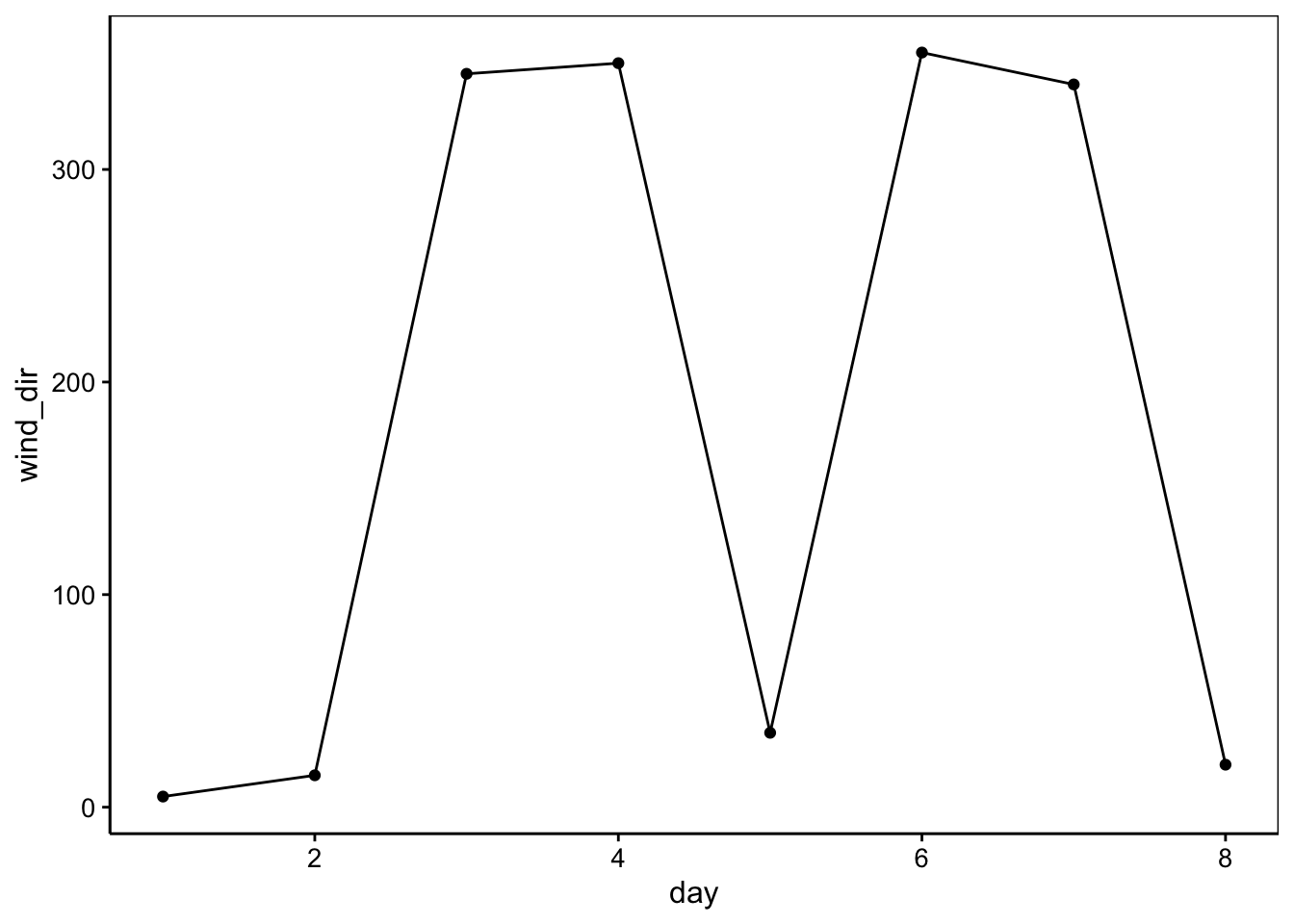
Nous avons effectivement l’impression d’une forte et brutale variation de la direction du vent sur ce graphique. Mais si nous nous rappelons qu’en fait 360° = 0°, alors, nous avons un sérieux problème. En effet, si nous avons les observations successives 0° et 360° (donc deux fois la même direction en fait), la moyenne sera : (0 + 360) / 2 = 180°, donc pile la direction opposée aux deux observations ! Clairement, avec les données circulaires, nous ne pouvons pas ignorer l’arithmétique particulière qui leur est associée. Des précautions sont également nécessaires pour représenter de telles données graphiquement.

Pour le graphique, nous utiliserons typiquement des coordonnées polaires pour enrouler les données sur elles-mêmes et faire coïncider, ici, 360° avec 0°. Le package {circular} propose des objets et des graphiques adaptés.

library(circular)
# 
# Attaching package: 'circular'
# The following objects are masked from 'package:stats':
# 
#     sd, var

Nous devons d’abord transformer notre variable en objet circular à l’aide de la fonction circular() (voir ?circular pour les détails concernant ses arguments) en wind_c.

meteo %>.%
  smutate(., wind_c = circular(wind_dir,
    units = "degrees", template = "geographics")) %->%
  meteo
meteo
#      day wind_dir     wind_c
#    <int>    <num> <circular>
# 1:     1        5          5
# 2:     2       15         15
# 3:     3      345        345
# 4:     4      350        350
# 5:     5       35         35
# 6:     6      355        355
# 7:     7      340        340
# 8:     8       20         20

En apparence, les données n’ont pas été modifiées, mais voyez en haut de colonne. wind_dir contient des valeurs numériques <dbl> pour doubles, des valeurs numériques à virgule flottante), alors que wind_c est de classe circular. La fonction plot() peut ensuite être appliquée sur cette nouvelle variable wind_c :

plot(meteo$wind_c)

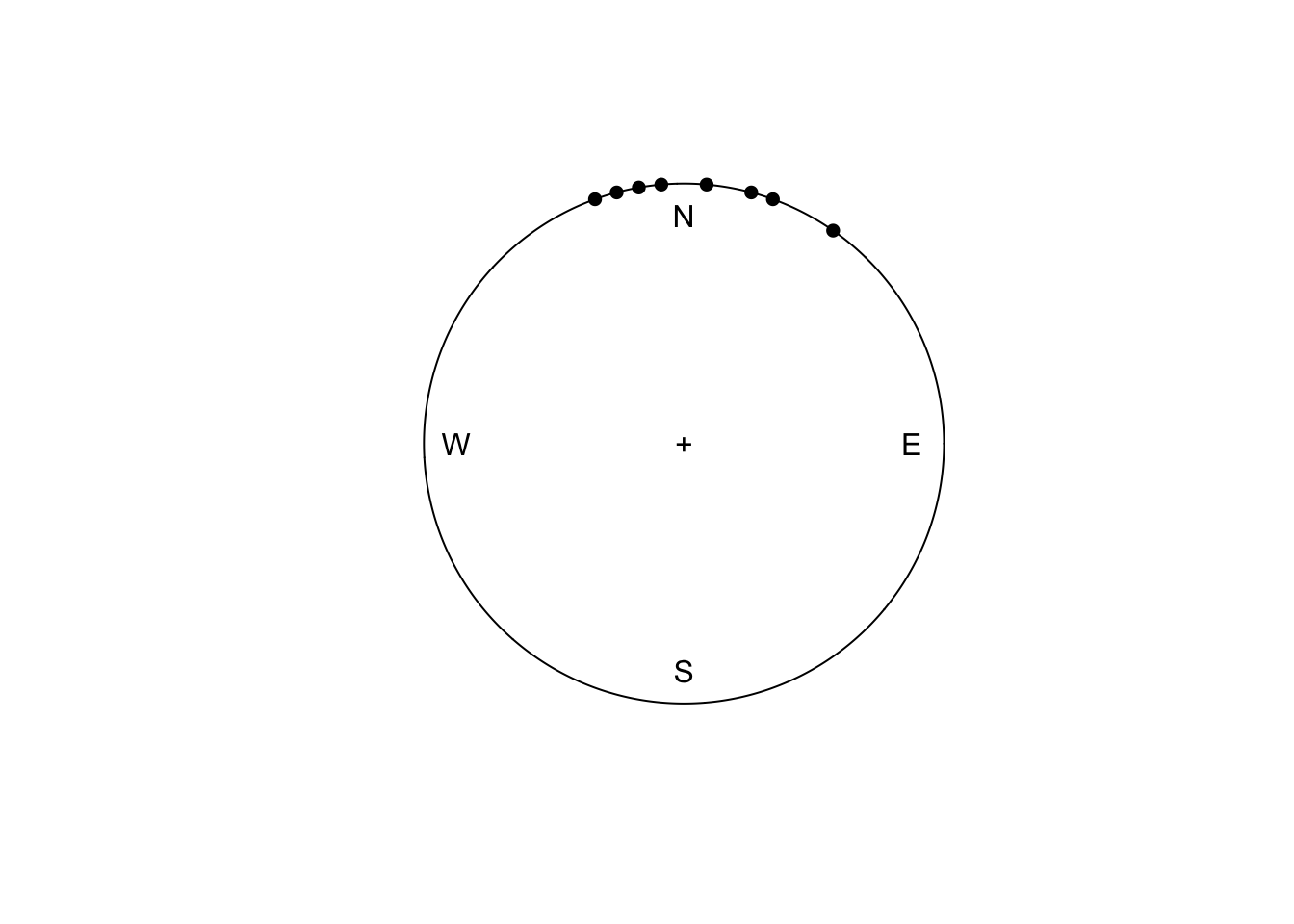
Nous voyons clairement ici que le vent que nous avons enregistré est toujours dirigé vers le nord, et jamais au sud comme notre moyenne naïve nous indiquait. À partir du moment où nous avons encodé notre variable de direction de vent correctement comme un objet circular, tout devient plus simple, car des calculs sont automatiquement adaptés :

mean(meteo$wind_c)
# Circular Data: 
# Type = angles 
# Units = degrees 
# Template = geographics 
# Modulo = asis 
# Zero = 1.570796 
# Rotation = clock 
# [1] 3.00925

Nous avons donc une moyenne de 3°, soit un vent effectivement orienté nord. De même l’écart type est bien plus petit que le calcul naïf nous faisait croire :

sd(meteo$wind_c)
# [1] 0.3127803

C’est la “magie” des objets S3 qui opère ici : les fonctions mean(), sd(), plot() sont dites fonctions génériques dont les méthodes varient en fonction de la nature (la classe) de l’objet passé comme premier argument. Le package {circular} implémente des versions particulières de ces fonctions qui tiennent compte des particularités des fonctions circulaires.

7.3.1 Hirondelles

Maintenant que nous avons compris cela, attaquons-nous à un cas un peu plus complexe. Des scientifiques étudient la capacité des hirondelles rustiques Hirundo rustica à se diriger dans leurs migrations grâce au champ magnétique terrestre. Ils capturent une centaine d’hirondelles en migration automnale près de Pise et les placent dans un dispositif qui modifie le champ magnétique terrestre de -90° (groupe shifted) ou non (groupe control). Ils mesurent la direction que prend chaque individu ensuite. Voyez ?swallows dans le package {circular} pour plus d’infos. L’objectif est ici de déterminer si les hirondelles utilisent le champ magnétique terrestre pour s’orienter lors de leurs migrations saisonnières.

swallows <- read("swallows", package = "circular")
swallows
#      treatment heading
#         <fctr>   <int>
#   1:   control     180
#   2:   control     142
#   3:   control      46
#   4:   control     124
#   5:   control      26
#  ---                  
# 110:   shifted     272
# 111:   shifted     323
# 112:   shifted     173
# 113:   shifted     285
# 114:   shifted     223

La variable heading est la direction initiale prise par chaque hirondelle en degré (0° = nord). Cette variable doit se traiter, donc, comme la direction du vent plus haut (actuellement elle est <int> pour integer, soit des valeurs numériques entières).

swallows <- smutate(swallows, heading = circular(heading,
  units = "degrees", template = "geographics"))
swallows
#      treatment    heading
#         <fctr> <circular>
#   1:   control        180
#   2:   control        142
#   3:   control         46
#   4:   control        124
#   5:   control         26
#  ---                     
# 110:   shifted        272
# 111:   shifted        323
# 112:   shifted        173
# 113:   shifted        285
# 114:   shifted        223

La variable treatment correspond aux deux traitements différents : control et shifted. Les hirondelles se répartissent comme ceci entre les traitements :

table(swallows$treatment)
# 
# control shifted 
#      66      48

Pour visionner ces données, nous utilisons l’argument stack = TRUE qui “empile” les données lorsqu’il y a plusieurs fois la même valeur. L’argument shrink= réduit la taille du cercle pour visualiser toutes les données.

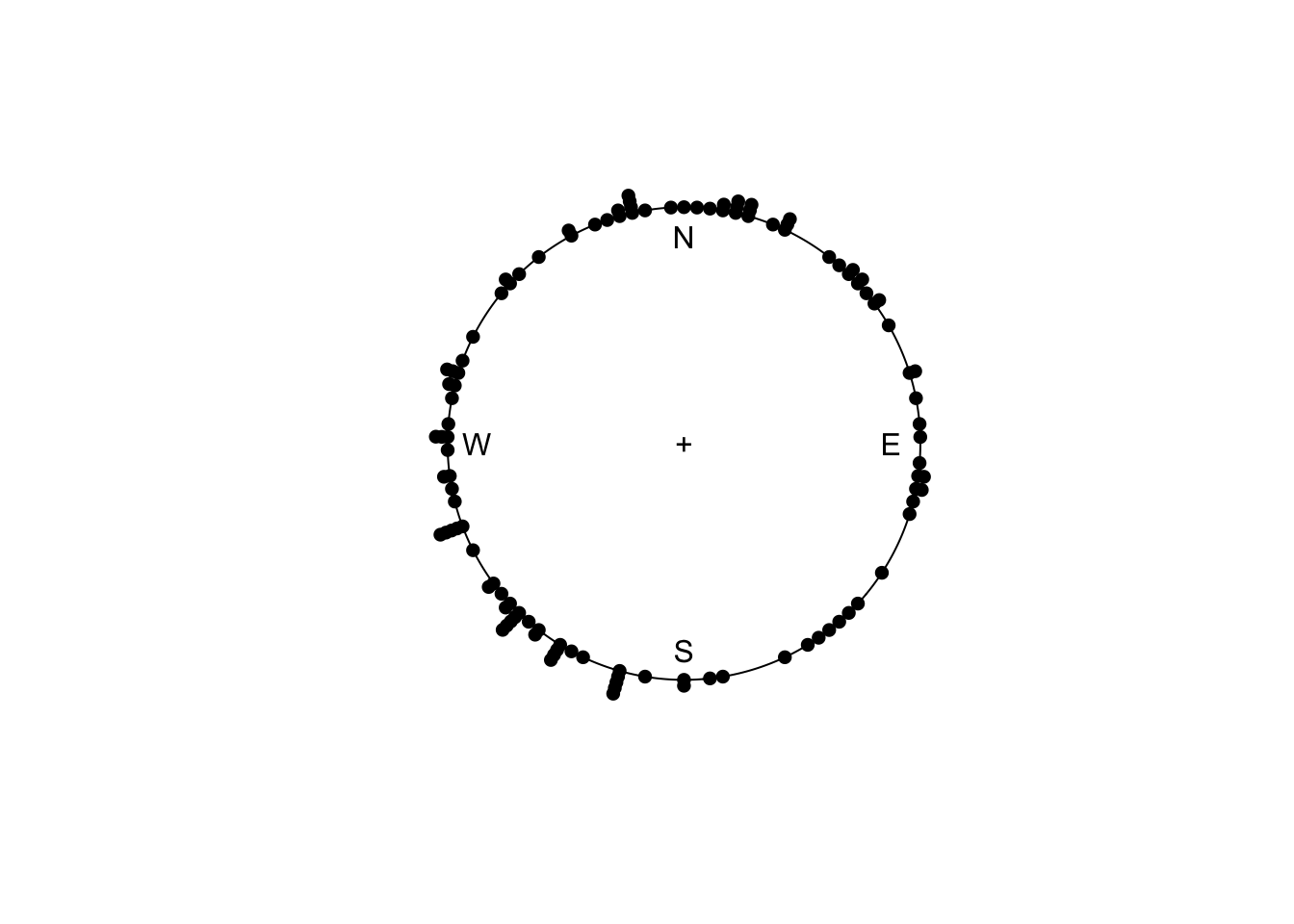
plot(swallows$heading, stack = TRUE, shrink = 1.1)

Nous voulons plutôt visualiser les données pour les deux traitements séparément. Malheureusement, les facettes ou autres astuces ne sont pas disponibles ici. Donc, nous devons ruser en réalisant séparément deux graphiques, en les combinant en une figure unique. Mais attention ! Ici, ce sont des graphiques de base. Donc, la combinaison se fait via la division de la zone du graphique en lignes et colonnes à l’aide de par(mfrow = c(<lignes>, <cols>)). Ici, nous souhaitons une ligne et deux colonnes. Nous diminuons également les marges avec mar=. Enfin, nous annotons les graphiques avec des flèches indiquant la direction moyenne des hirondelles dans chaque traitement à l’aide de arrows.circular().

par(mfrow = c(1, 2), mar = c(0, 0, 1.1, 0))

# Contrôles
swallows_c <- sfilter(swallows, treatment == "control")
plot(swallows_c$heading, stack = TRUE, shrink = 1, col = "darkblue",
    main = "Contrôle")
arrows.circular(mean(swallows_c$heading), col = "darkblue")

# Désorientées
swallows_s <- sfilter(swallows, treatment == "shifted")
plot(swallows_s$heading, stack = TRUE, shrink = 1, col = "darkred",
    main = "Désorientée")
arrows.circular(mean(swallows_s$heading), col = "darkred")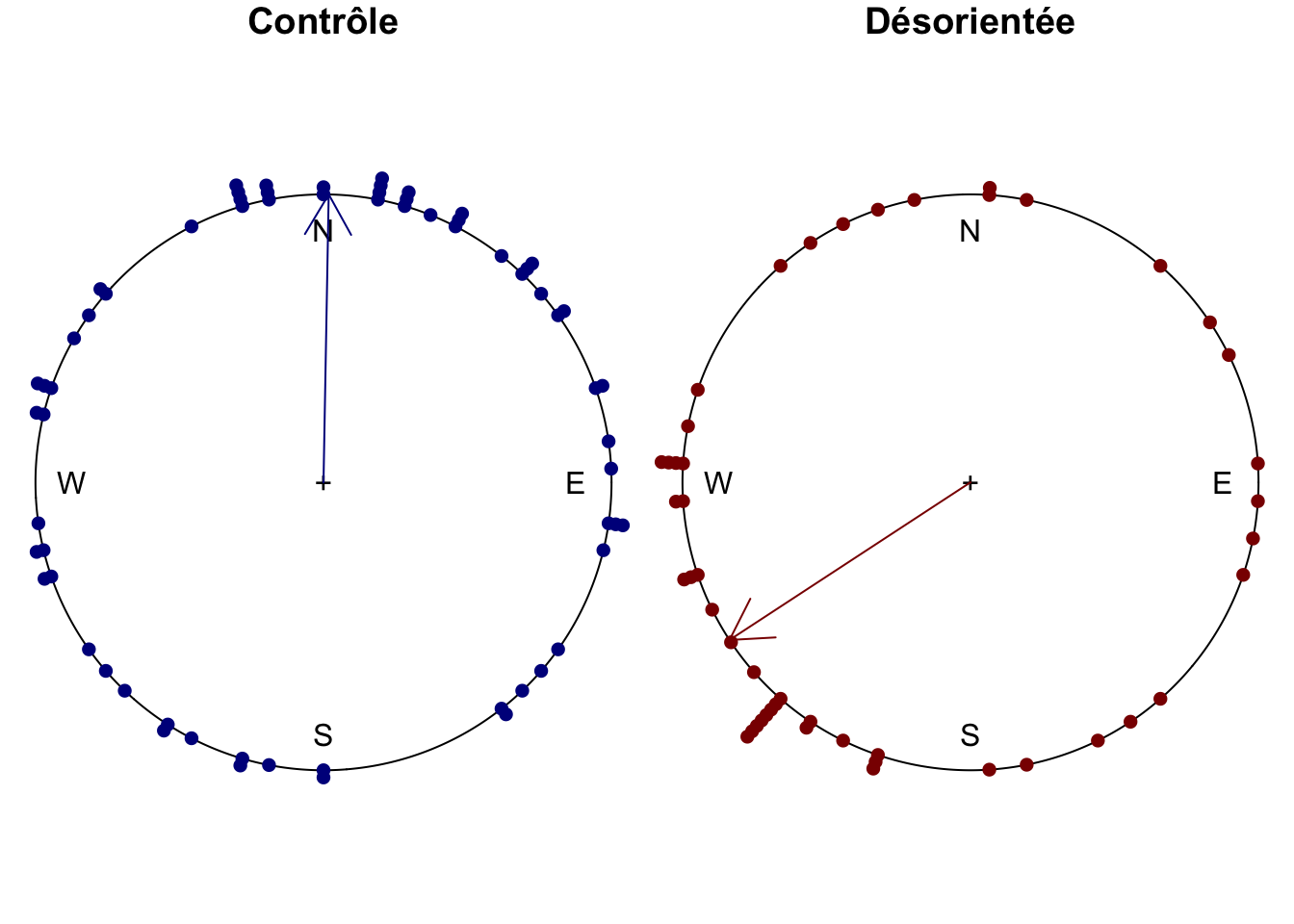

Sur les graphiques, il semble bien que les hirondelles désorientées prennent un cap différent. À ce stade, nous avons besoin d’un test d’hypothèse. Mais ici aussi, les calculs doivent tenir compte des particularités des variables circulaires. Pour une ANOVA à un facteur, {circular} nous gratifie encore une fois d’une fonction adaptée via aov.circular() :

aov.circular(swallows$heading, group = swallows$treatment)
# 
# Call:
# aov.circular(x = swallows$heading, group = swallows$treatment)
# 
# 
#  Circular Analysis of Variance: High Concentration F-Test 
#  
#          df    SS      MS     F         p
# Between   1 16.83 16.8308 55.03 2.453e-11
# Within  112 81.96  0.7318    NA        NA
# Total   113 98.79  0.8742    NA        NA
# 
#

Le tableau de l’ANOVA diffère légèrement, néanmoins nous reconnaissons sa structure classique. La valeur F vaut 55,03 et la valeur p dans la dernière colonne est très faible, et certainement inférieure à un seuil \(\alpha\) classique de 5%. Les directions moyennes prises par les hirondelles sont donc significativement différentes entre les deux traitements au seuil \(\alpha\) de 5%. Ceci démontre que ces hirondelles utilisent le champ magnétique terrestre pour s’orienter.

Vous avez maintenant compris le principe : avec des variables circulaires, nous devons prendre des précautions particulières. Mais à condition d’utiliser les versions graphiques et numériques adaptées, nous pouvons analyser alors correctement nos données.

Les variables circulaires ne sont pas limitées à une orientation dans l’espace. Les cycles (circadiens, saisonniers …) peuvent aussi être analysés à l’aide de ce type de variable. En réalité, tout ce qui est cyclique le peut. Par exemple, les huîtres suivent un cycle de croissance gonadique, maturation, ponte, et enfin résorption des gonades lors d’un cycle sexuel. Si les différents stades sont exprimés numériquement (stade 1 à stade 5, le stade 5 étant égal au stade 0), nous pourrons traiter également cette information sous forme d’une variable circulaire. Nous devons juste être attentifs à utiliser les bons arguments dans son encodage à l’aide de la fonction circular().

Outre une orientation dans l’espace avec template = "geographics", circular() prend aussi automatiquement en compte les cycles circadiens avec template = "clock24". Voici, par exemple, des données concernant l’heure d’arrivée aux urgences de patients sur une période de 12 mois.

hospital <- dtx(admission = read("fisherB1", package = "circular"))
hospital
#      admission
#          <num>
#   1:     11.00
#   2:     17.00
#   3:     23.15
#   4:     10.00
#   5:     12.00
#  ---          
# 250:     20.00
# 251:      2.00
# 252:      1.45
# 253:      1.45
# 254:      2.05

Nous convertissons en variable circulaire comme ceci :

hospital %<-% mutate(hospital, admission_c = circular(admission,
  units = "hours", template = "clock24"))
hospital
#      admission admission_c
#          <num>  <circular>
#   1:     11.00       11.00
#   2:     17.00       17.00
#   3:     23.15       23.15
#   4:     10.00       10.00
#   5:     12.00       12.00
#  ---                      
# 250:     20.00       20.00
# 251:      2.00        2.00
# 252:      1.45        1.45
# 253:      1.45        1.45
# 254:      2.05        2.05

Effectuons maintenant un graphique différent : un histogramme en coordonnées polaires (appelé rose diagramme en anglais).

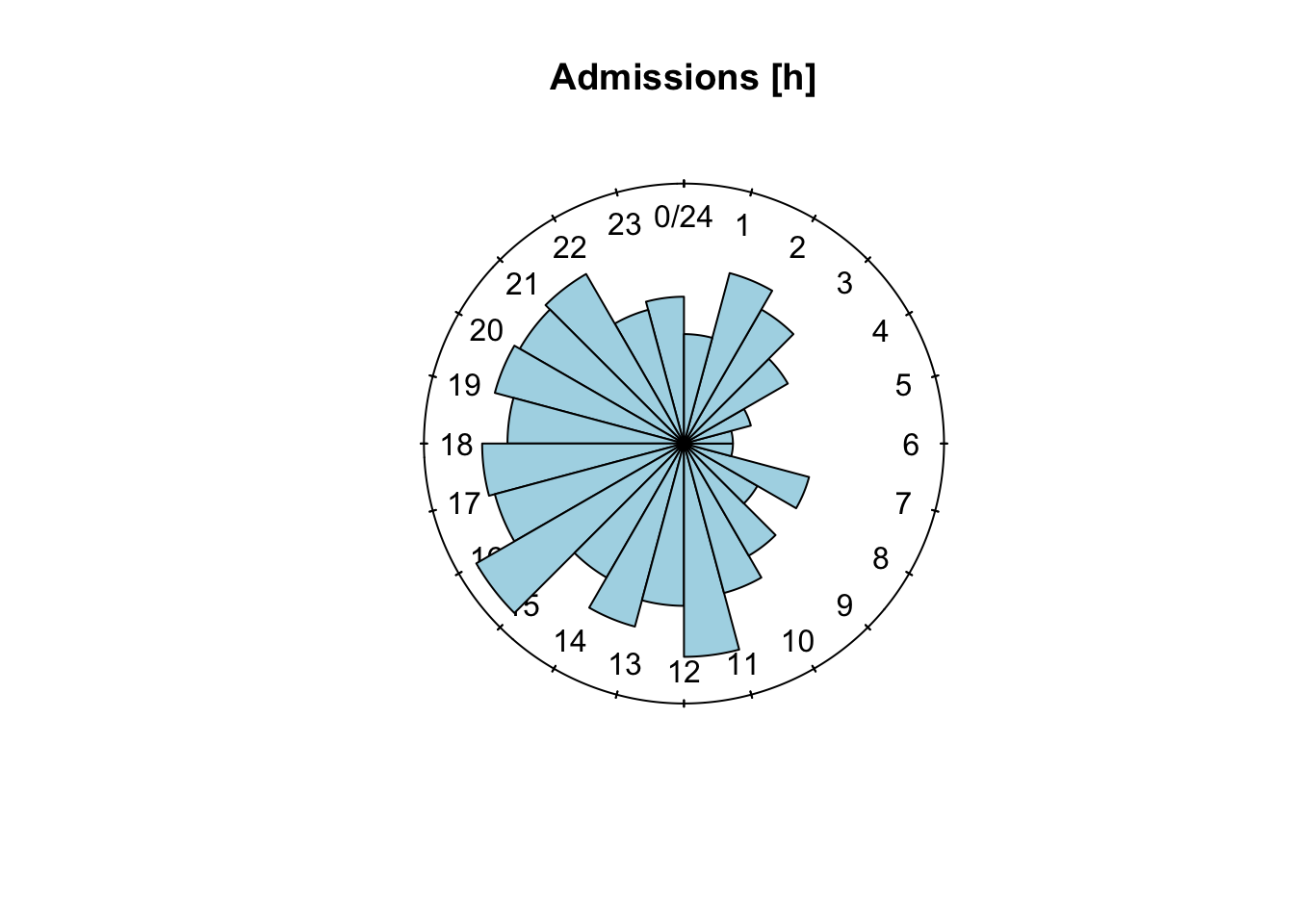
rose.diag(hospital$admission_c, bin = 24, col = "lightblue",
  main = "Admissions [h]", prop = 3)

Nous pouvons obtenir un graphique très similaire avec chart() (notez que les limites des classes diffèrent légèrement).

chart(data = hospital, ~admission_c) +
  geom_histogram(bins = 24, center = 0.5, fill = "lightblue", col = "black") +
  coord_polar(start = 0) +
  scale_x_continuous(breaks = c(0, 3, 6, 9, 12, 15, 18, 21)) +
  theme_minimal() +
  xlab("Admissions [h]") +
  ylab("Dénombrement")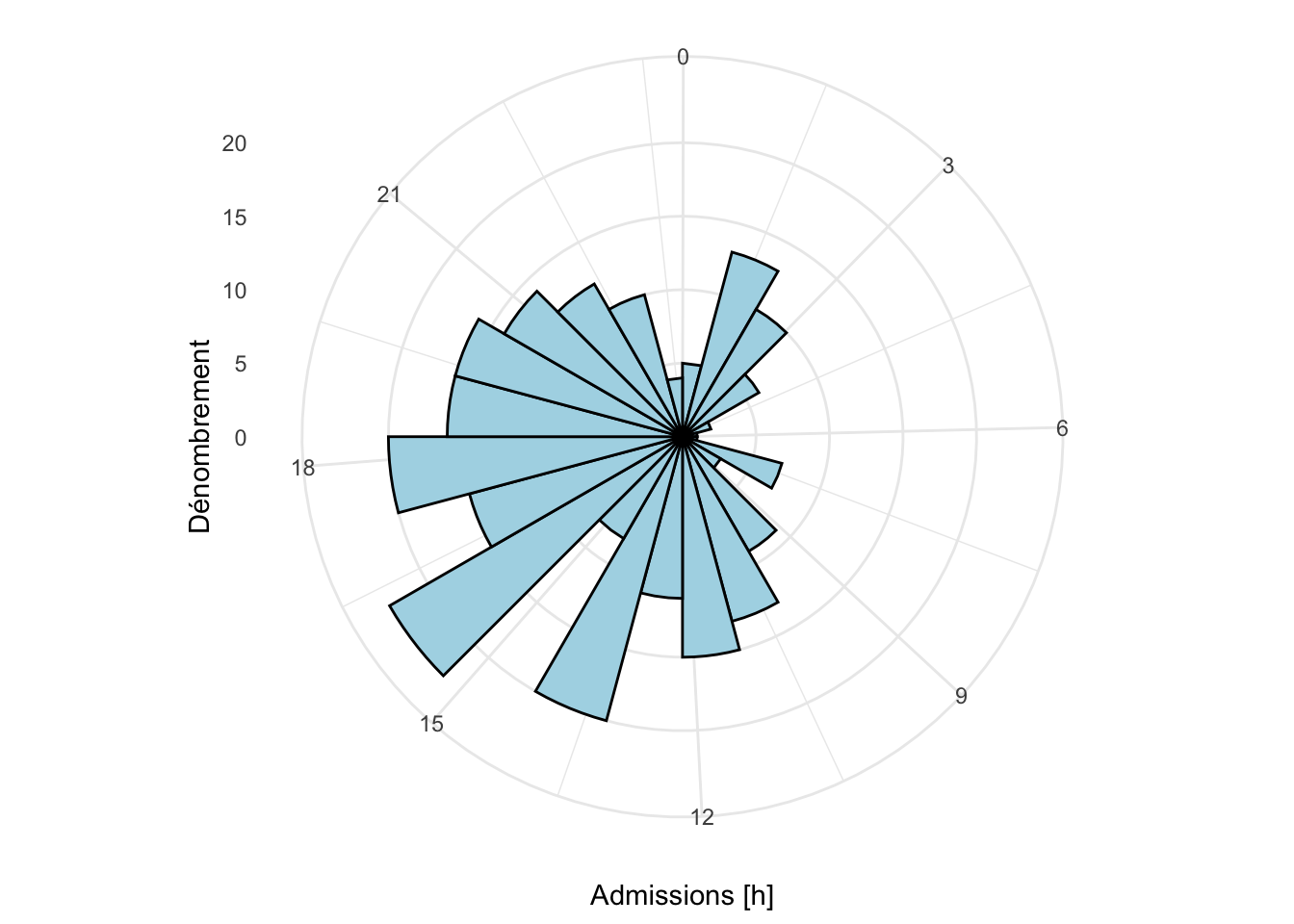

Le graphique chart() utilise une échelle linéaire, alors que rose.diag() utilise par défaut une transformation racine carrée. Pour obtenir un graphique similaire, nous ferons donc (toujours pas parfaitement identique, car les limites des classes sont toujours différentes) :

rose.diag(hospital$admission_c, bin = 24, col = "lightblue",
  main = "Admissions [h]", prop = 9, radii.scale = "linear")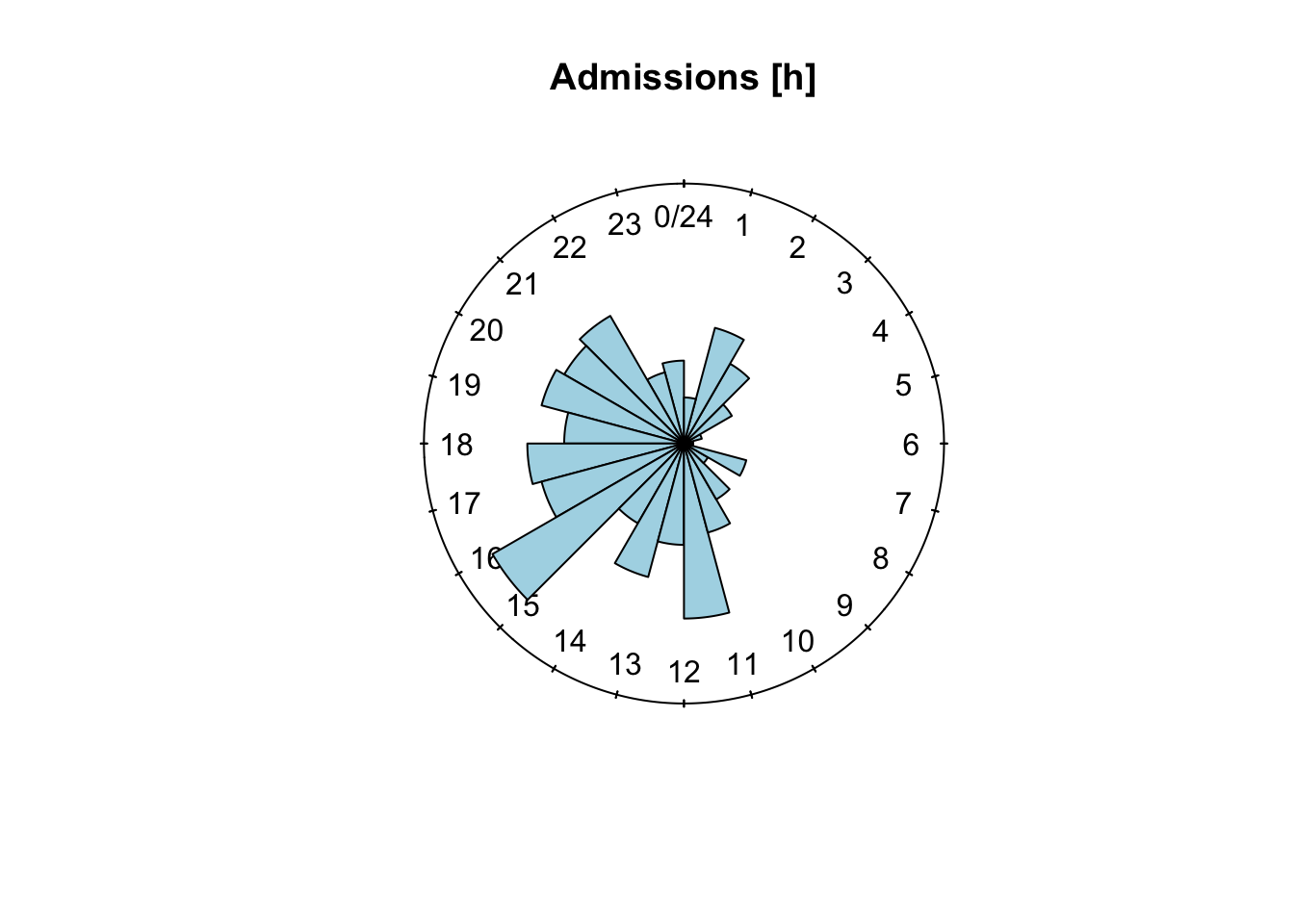

Pour d’autres types de données, nous devons spécifier complètement le système que nous souhaitons utiliser. Pour nos huîtres qui présentent cinq stades de maturité de leurs gonades, nous ferions (données générées artificiellement) :

set.seed(37843)
oysters <- dtx(
  maturity = sample(1:5, 40, replace = TRUE))
oysters
#     maturity
#        <int>
#  1:        3
#  2:        5
#  3:        2
#  4:        5
#  5:        5
#  6:        3
#  7:        2
#  8:        3
#  9:        1
# 10:        2
# 11:        5
# 12:        4
# 13:        3
# 14:        5
# 15:        4
# 16:        4
# 17:        3
# 18:        1
# 19:        1
# 20:        3
# 21:        4
# 22:        5
# 23:        2
# 24:        5
# 25:        5
# 26:        1
# 27:        5
# 28:        2
# 29:        4
# 30:        2
# 31:        2
# 32:        5
# 33:        5
# 34:        2
# 35:        5
# 36:        4
# 37:        4
# 38:        2
# 39:        3
# 40:        3
#     maturity

Nous pouvons visualiser la distribution en ces cinq stades comme ceci :

chart(data = oysters, ~ maturity) +
  geom_bar(width = 1, fill = "cornsilk", col = "black") +
  coord_polar(start = 0) +
  scale_x_continuous(breaks = c(1, 2, 3, 4, 5)) +
  theme_minimal() +
  xlab("Maturity stage") +
  ylab("Dénombrement")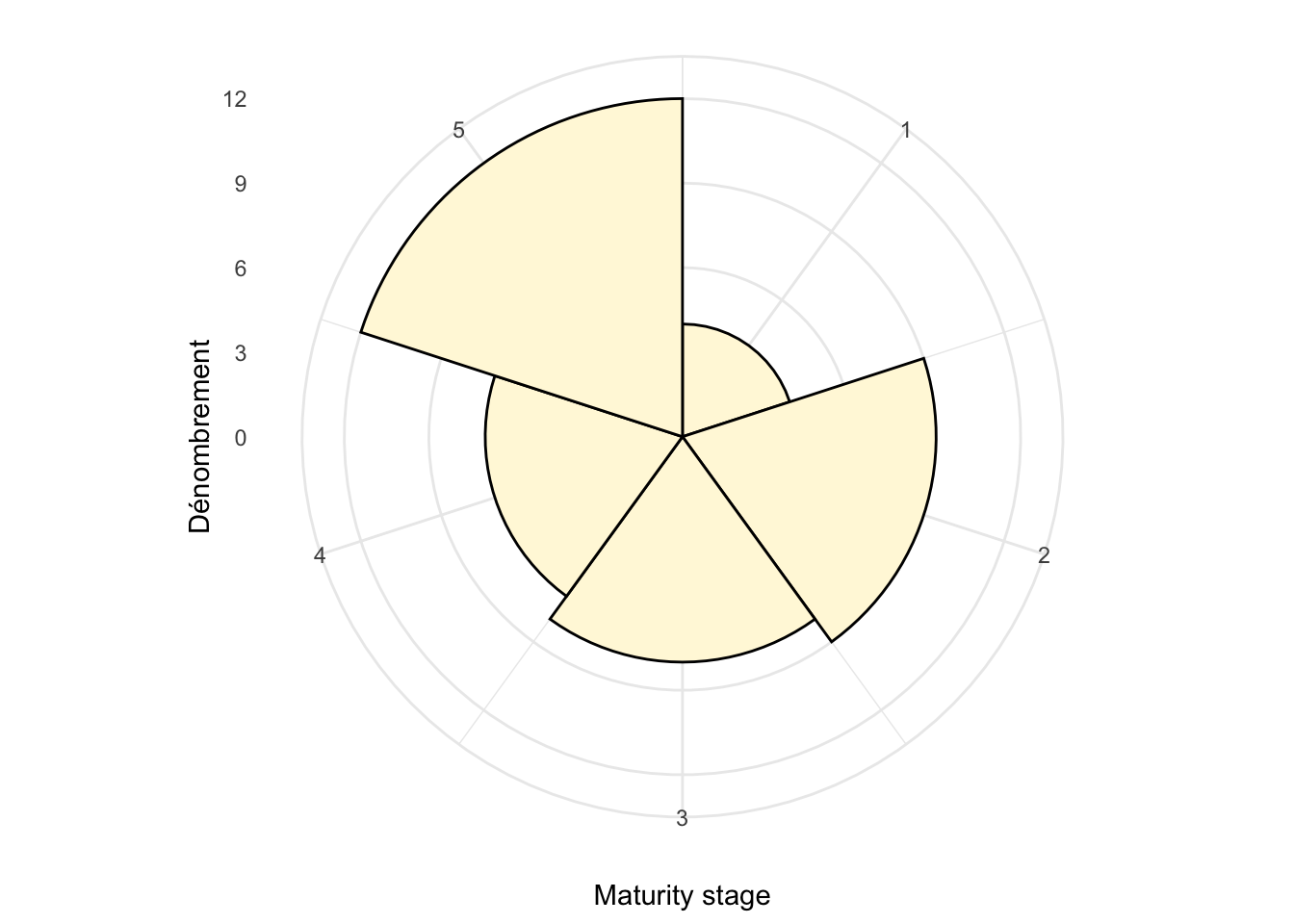

Pour convertir cette variable maturity en variable circulaire, nous ne possédons pas de template. Nous devons convertir nos valeurs de 1 à 5 en radians (en divisant par la valeur max et en multipliant par \(2 \pi\)).

oysters %<-% mutate(oysters, maturity_c = circular(maturity/5 * 2*pi,
  rotation = "clock", zero = pi/2))
oysters
#     maturity maturity_c
#        <int> <circular>
#  1:        3   3.769911
#  2:        5   6.283185
#  3:        2   2.513274
#  4:        5   6.283185
#  5:        5   6.283185
#  6:        3   3.769911
#  7:        2   2.513274
#  8:        3   3.769911
#  9:        1   1.256637
# 10:        2   2.513274
# 11:        5   6.283185
# 12:        4   5.026548
# 13:        3   3.769911
# 14:        5   6.283185
# 15:        4   5.026548
# 16:        4   5.026548
# 17:        3   3.769911
# 18:        1   1.256637
# 19:        1   1.256637
# 20:        3   3.769911
# 21:        4   5.026548
# 22:        5   6.283185
# 23:        2   2.513274
# 24:        5   6.283185
# 25:        5   6.283185
# 26:        1   1.256637
# 27:        5   6.283185
# 28:        2   2.513274
# 29:        4   5.026548
# 30:        2   2.513274
# 31:        2   2.513274
# 32:        5   6.283185
# 33:        5   6.283185
# 34:        2   2.513274
# 35:        5   6.283185
# 36:        4   5.026548
# 37:        4   5.026548
# 38:        2   2.513274
# 39:        3   3.769911
# 40:        3   3.769911
#     maturity maturity_c

Le graphique par défaut de {circular} est moins bien que la version chart() de l’histogramme avec coordonnées polaires.

#plot(oysters$maturity_c, stack = TRUE, shrink = 1.1)
rose.diag(oysters$maturity_c, bins = 5, col = "cornsilk", prop = 3, radii.scale = "linear", axes = FALSE)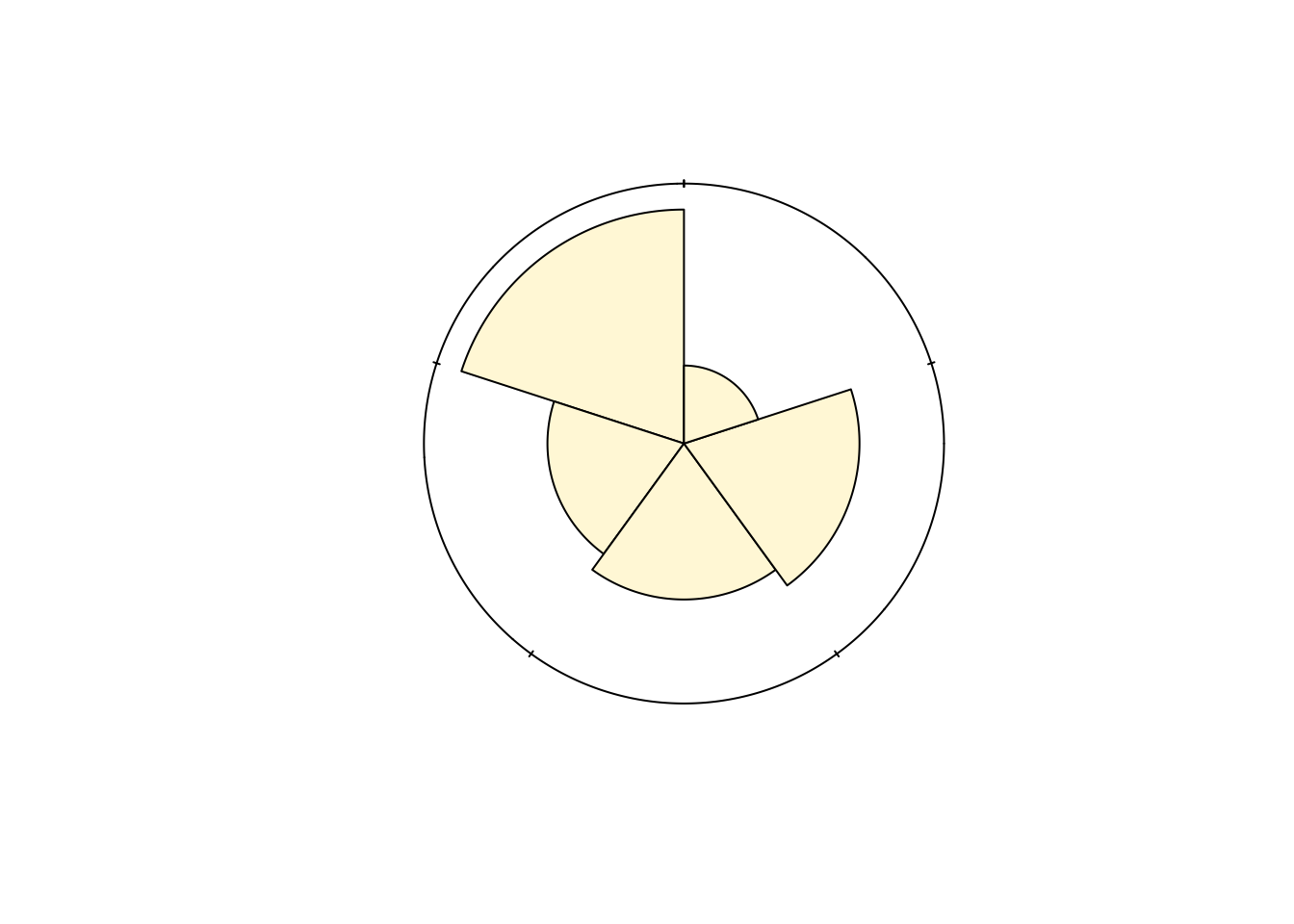

À vous de jouer !

Réalisez le travail D07Ia_data, partie II.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md, partie II.

Pour en savoir plus