A.4 Bases du langage R

A.4.1 Quelques notions sur les variables

Voici quelques notions élémentaires concernant les variables dans le langage R.

Les vecteurs et matrices numériques de dimension deux ou au-delà sont les variables de base. Les nombres qu’ils contiennent sont complétés de quelques valeurs spéciales : NA, ainsi que NaN, -Inf et Inf. NA pour “Not Available” indique un trou ou une valeur manquante dans un jeu de données. NaN pour “Not a Number” indique le résultat d’une opération qui ne renvoie pas un nombre. La plupart du temps, il est traité comme NA. -Inf et Inf se passent de tout commentaire… Entrez par exemple successivement B <- c(1, 2, NA, 3), B^2, 0/0, log(0). Notez que dans beaucoup de langages “non scientifiques”, les deux dernières commandes provoquent des erreurs… alors que dans R, elles sont traitées correctement.
Il existe bien sûr des chaînes de caractères qui peuvent être traitées également sous forme de vecteurs ou de matrices. Ex : A <- c("oui", "non", "peut-être"), paste("Alors, c'est", A, "?").
Les tests logiques et les valeurs logiques TRUE et FALSE existent aussi. Essayez par exemple 1 == 2/2, log(5) > 2, 1:5 >= 3, A <- c(TRUE, TRUE, FALSE), A != TRUE, !A (le test d’égalité se note ==; le test d’inégalité est !=; <= veut dire inférieur ou égal à, >= signifie supérieur ou égal à, < et > sont les opérateurs inférieur à et supérieur à, respectivement, et ! est l’opérateur de négation, c’est-à-dire : ce qui est vrai devient faux et vice versa). Notez au passage les variables spéciales TRUE et FALSE. Ce sont des mots réservés du langage, au même titre que if, else, while, etc., et qui ne peuvent pas être utilisé comme noms de variables.

Les variables TRUE et FALSE peuvent aussi s’abréger en T et F. Par contre, contrairement aux premières, T et F ne sont pas des mots réservés, et leur utilisation peut donc s’avérer dangereuse dans le cas ou l’on assigne d’autres valeurs à ces variables. Il est par exemple parfait permis de faire les assignations suivantes : T <- FALSE; F <- TRUE. Donc, maintenant, TRUE est FALSE et FALSE est TRUE partout où vous utilisez T et F ! Allez donc débusquer ce genre d’erreur dans plusieurs centaines de lignes de code si vous prenez la (mauvaise) habitude d’utiliser T et F à tour de bras. Pour cette raison, l’utilisation de T et F dans le code des packages est interdite depuis la version 1.6.0 de R et est sanctionnée par un message d’erreur à la compilation du package… Donc, autant prendre tout de suite de bonnes habitudes. Le jour où vous compilerez vos propres packages, ce ne sera alors plus un problème pour vous.

Les matrices sont créées entre autres à l’aide des fonctions matrix() pour deux dimensions et array() au-delà, et indexées à l’aide de []. Entrez A <- matrix(1:6, dim = c(2, 3)); A (notez que le premier indice représente les lignes et le second indice représente les colonnes). Pour comprendre comment récupérer et/ou modifier des éléments de cette matrice, étudiez l’effet des instructions suivantes A[1, 2], A[ , 3], B <- A[2, 2:3]; B, A[1, 2] <- 0; A.
En réalité, les variables R peuvent être incroyablement plus complexes : elles peuvent être des variables objets qui ont une classe et des méthodes déterminées (nous verrons cela plus loin), elles peuvent comporter différents attributs, les lignes et les colonnes peuvent avoir des noms et elles peuvent même contenir du code exécutable, voire tout un environnement de travail (si, si) ! Étudions maintenant les attributs et les noms de lignes et de colonnes. attributes(A) liste tous les attributs de la variable A (on voit que les dimensions de la matrice sont un attribut). Pour ajouter un attribut, on utilise attr(var, "attribut"). Entrez à titre d’exemple attr(A, "commentaire") <- "Une matrice exemple...", puis faites à nouveau attributes(A), et ensuite A. Vous pouvez ajouter autant d’attributs que vous voulez à une variable. Certains attributs, tels que "dim" ne sont pas listés lorsqu’on interroge la variable. Les attributs “exotiques” sont, quant à eux, listés après le contenu de la variable elle-même.
Autre propriété utile, vous pouvez nommer les lignes et les colonnes d’une matrice. Par exemple, tapez successivement colnames(A) <- c("col1", "col2", "col3"), rownames(A) <- c("ligne1", "ligne2"), A. Pour nommer les éléments d’un vecteur, on utilisera plutôt la fonction names(), tout simplement. Entrez à présent A[, "col2"]. Vous voyez que, une fois que vous avez nommé des colonnes, vous pouvez utiliser ces noms pour les sélectionner dans la matrice, en lieu et place de leur numéro.
Il y a encore plusieurs autres types de variables que nous ne verrons pas ici (consultez les manuels de R installés avec le logiciel). Un autre type de variable mérite toutefois notre attention, car il est très important, il s’agit des objets list. Une liste est en fait le rassemblement de plusieurs variables sous une seule. Elle permet donc de rassembler plusieurs éléments qui ont un lien entre eux et donc, d’organiser de façon logique vos données. Vous comprendrez sans doute mieux sur base d’un exemple. Entrez l’instruction suivante B <- list(name = "Jack", age = 50, nombre.d.enfants = 3, age.enfants = c(2, 5, 10)); B. Pour accéder à un élément d’une liste, on utilise list$element. Par exemple: B$age ou B$age.enfants[2].

Comme on peut le voir, les moyens de stocker et de manipuler les données dans R sont extrêmement nombreux et souples… Au chapitre suivant, nous étudierons de manière plus extensive le type de données data frame qui est le type par excellence pour représenter un tableau de données statistiques brutes, et par là même, le moyen privilégié pour importer et exporter les données de et vers d’autres logiciels.

A.4.2 Le data frame

Le type de données de base utilisées en statistiques est souvent décrit comme un tableau bidimensionnel “cas versus variables”. Chaque ligne représente un “cas” (ou individu, quadras, station, etc.) et chaque colonne représente une variable (c’est-à-dire, une “caractéristique”, ou mesure qualitative, semi-quantitative, voire quantitative effectuée sur les différents cas). À première vue, s’agissant d’un tableau bidimensionnel, on doit pouvoir représenter ce type de données dans une matrice numérique… d’autant plus que R permet de nommer les lignes et les colonnes, ce qui facilite le repérage des différentes entités. En fait, c’est souvent plus compliqué ! Les différentes variables peuvent en effet être de nature différente : numériques (entières, voire réelles ou même complexes, ou encore sous forme de dates), semi-quantitatives ou sous forme de classe (comme “petit”/“moyen”/“grand”, “présent”/“absent”, “bleu”/“vert”/“jaune”, etc.), voire textuelles (le nom d’une espèce, d’un lieu, etc.). Or il n’est pas possible de rassembler tous ces types différents dans une seule matrice, parce qu’une matrice n’admet qu’un seul type de données dans toutes ses colonnes. Pour palier à cette limitation, R utilise le data frame qui permet de choisir librement le contenu de chaque colonne.

Pour voir un exemple de data frame avec des variables de type différent, ouvrez le fichier de données exemple ToothGrowth qui correspond à une étude de l’effet de la vitamine C sur la croissance des dents de cobayes (donc, un sujet qui nous passionne tous, bien entendu). Pour cela, faites data(ToothGrowth) et visionnez le fichier en entrant ToothGrowth.
R permet d’éditer ce type de fichier à la manière d’un tableur grâce aux fonctions edit() et fix(). Sous Windows, on peut aussi utiliser l’entrée de menu Edit -> Data editor.... On peut par précaution sauver le tableau modifié dans une autre variable, à l’aide de l’instruction var.new <- edit(var.orig). De même, on peut créer un tableau vide que l’on remplira à la main grâce à var <- edit(data.frame()). Pour éditer le tableau ToothGrowth et sauver les modifications dans la variable myToothGrowth, entrez myToothGrowth <- edit(ToothGrowth), modifiez quelques valeurs et fermez le tableur. Ensuite, vérifiez que vos modifications sont bien enregistrées dans la variable myToothGrowth en tapant son nom à la ligne de commande.
Pour exporter votre tableau modifié dans un format lisible par n’importe quel autre logiciel, utilisez la fonction write.table(). Cette fonction a une syntaxe complexe qui reflète les nombreuses possibilités qu’elle offre pour formater le fichier créé (faites ?write.table pour prendre connaissance de ces options). Nous allons simplement exporter notre tableau avec les options par défaut dans le répertoire “c:\temp”. Pour cela, entrez write.table(myToothGrowth, file = "c:/temp/mytable.txt") (n’oubliez pas d’utiliser le slash / à la place du backslash \ pour indiquer l’arborescence des répertoires). Ouvrez maintenant l’explorateur de Windows et vérifiez que le fichier a bien été créé. Double-cliquez dessus pour l’ouvrir dans Notepad. Si vous disposez d’Excel sur votre ordinateur, vous pouvez le lancer pour y ouvrir le fichier créé et vérifier qu’Excel peut également le lire.
La fonction jumelle pour lire un tableau dans un fichier ASCII est read.table() (avec d’ailleurs autant d’options). Faites myTable <- read.table("c:/temp/mytable.txt") pour relire le fichier et l’inclure dans la variable myTable. Ensuite, listez cette variable (entrez myTable) pour vérifier le résultat.
Remarque : afin de faciliter l’importation de fichiers utilisant différents séparateurs de champs et différentes décimales, d’autres fonctions d’importation existent qui vous permettent de lire ces différents fichiers sans devoir modifier constamment les valeurs par défaut des paramètres de la fonction. Ainsi read.csv() lit des fichiers séparés par des virgules et ayant un point comme séparateur décimal. read.cvs2() lit des fichiers dont les champs sont séparés par un point virgule et dont la virgule sert de séparateur décimal. Enfin, read.delim() et read.delim2() importent des fichiers textes avec la tabulation comme séparateur de champ (se note \t), et respectivement le point ou la virgule comme séparateur décimal. Pour plus d’informations, voyer l’aide en ligne, ?read.table.
Pour finir, effacez vos variables myToothGrowth et myTable par rm(myToothGrowth, myTable). Vous pouvez effacer le fichier créé directement depuis R grâce à l’instruction file.remove("c:/temp/mytable.txt").

A.4.3 Distributions statistiques

Tout logiciel statistique qui se respecte se doit de posséder des fonctions pour générer aléatoirement des nombres selon différentes distributions statistiques (Normale, Chi², binomiale, etc.), et pour obtenir les probabilités associées à de telles distributions. R n’échappe pas à cette règle, et naturellement (richesse fonctionnelle oblige), il offre même beaucoup plus de distributions que les classiques (distributions multinormales, Cauchy, Weibull, Wilcoxon…) soit de base, soit dans des packages additionnels. Nous n’aborderons ici que les rudiments concernant les distributions statistiques, leurs analyses et leurs représentations graphiques.

Pour générer aléatoirement des nombres ayant une distribution normale de moyenne nulle et d’écart type unité, on utilise la fonction rnorm(). Exemple pour 100 valeurs aléatoires A <- rnorm(100). Faites ensuite successivement mean(A) (moyenne) et sd(A) (écart type) puis plot(A), hist(A), boxplot(A) et qqnorm(A); qqline(A).
Étudions un autre exemple de distribution, plus complexe cette fois-ci (l’exemple est tiré de “An Introduction to R” qui accompagne votre version du logiciel) :

library(pastecs)
data(faithful)
attach(faithful)
summary(eruptions)

#    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#   1.600   2.163   4.000   3.488   4.454   5.100

fivenum(eruptions)

# [1] 1.6000 2.1585 4.0000 4.4585 5.1000

stem(eruptions)

# 
#   The decimal point is 1 digit(s) to the left of the |
# 
#   16 | 070355555588
#   18 | 000022233333335577777777888822335777888
#   20 | 00002223378800035778
#   22 | 0002335578023578
#   24 | 00228
#   26 | 23
#   28 | 080
#   30 | 7
#   32 | 2337
#   34 | 250077
#   36 | 0000823577
#   38 | 2333335582225577
#   40 | 0000003357788888002233555577778
#   42 | 03335555778800233333555577778
#   44 | 02222335557780000000023333357778888
#   46 | 0000233357700000023578
#   48 | 00000022335800333
#   50 | 0370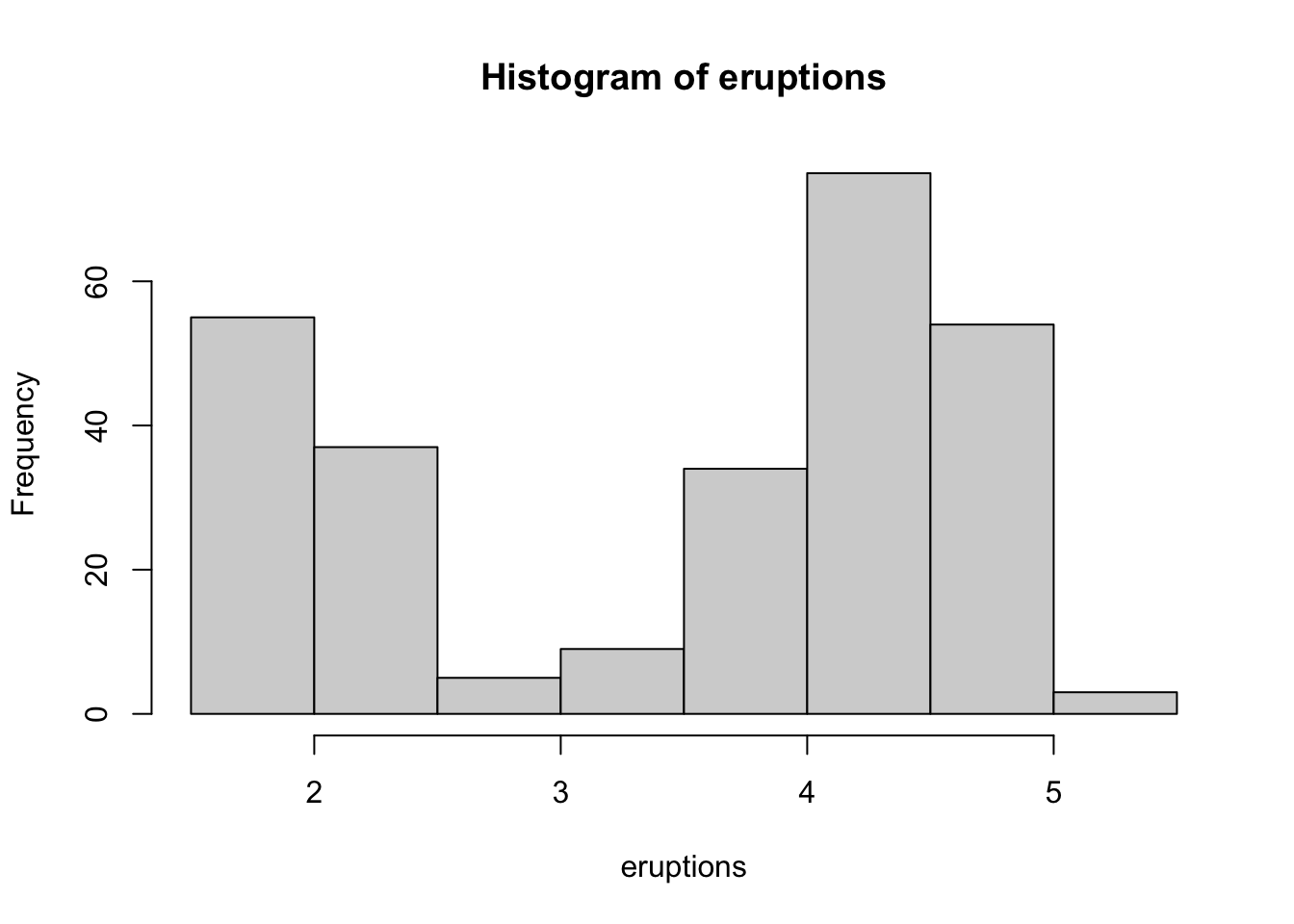

hist(eruptions)

Pour obtenir une plus belle représentation graphique de l’histogramme de cette distribution, y compris une estimation de sa densité lissée, vous pouvez utiliser :

hist(eruptions, seq(1.6, 5.2, 0.2), prob = TRUE, col = 7)
lines(density(eruptions, bw = 0.1), lwd = 2, col = 4)
rug(eruptions)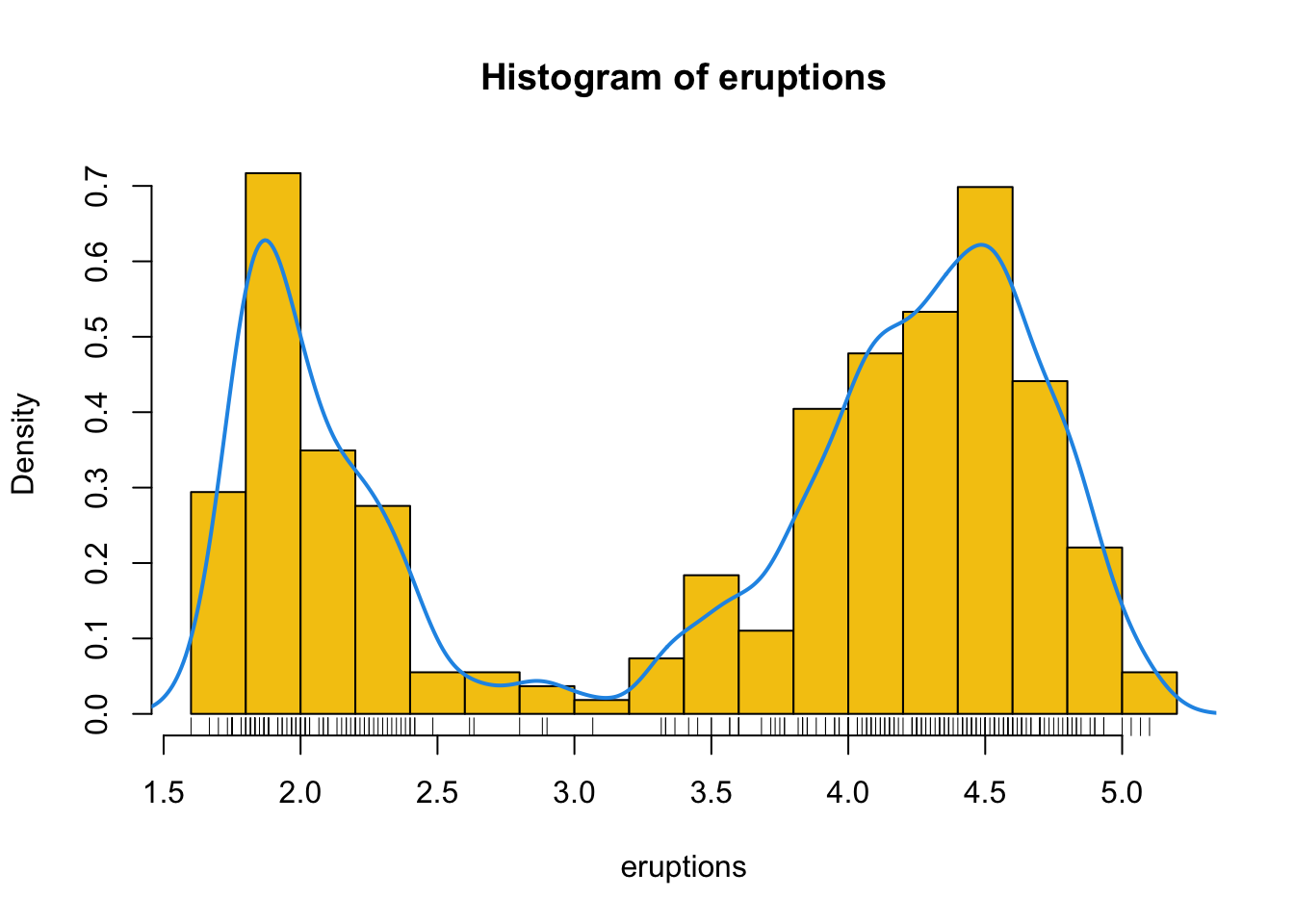

A.4.4 Deux exemples d’analyses dans R

Je vous propose maintenant de réaliser deux analyses classiques : une analyse en composantes principales et une classification du jeu de données marbio disponible dans le package {pastecs}. Vous verrez ainsi comment la logique objet s’articule dans R : une première fonction crée un objet qui contient tout ce qu’il faut pour poursuivre l’analyse, voire en faire des présentations graphiques de différentes façons… Et c’est l’utilisateur qui décide, en appelant telle ou telle fonction de ce qu’il veut obtenir ensuite. On est très loin ici du déballage systématique d’une ribambelle de résultats à la suite d’une commande unique, en espérant que l’utilisateur trouvera ce qui l’intéresse parmi tout cela, comme c’est le cas dans beaucoup d’autres logiciels statistiques ! Naturellement, puisque l’utilisateur est véritablement aux commandes de son analyse, il doit à tout moment savoir exactement ce qu’il fait. Ceci est souvent vu comme un désavantage, et se traduit par l’expression “trop complexe” dans la bouche de certains, alors même qu’en fait cette organisation ne présente pratiquement que des avantages et force l’utilisateur à bien comprendre les tenants et les aboutissants de son analyse.

Chargez le package {pastecs} et le jeu de données marbio par library(pastecs) et data(marbio).
Pour effectuer l’ACP, vous rentrerez :

marbio_pca <- princomp(log(marbio + 1), cor = TRUE)
summary(marbio_pca)

# Importance of components:
#                           Comp.1    Comp.2    Comp.3     Comp.4     Comp.5
# Standard deviation     3.1752223 1.7871712 1.4611111 1.40567650 1.04515773
# Proportion of Variance 0.4200849 0.1330825 0.0889519 0.08233027 0.04551478
# Cumulative Proportion  0.4200849 0.5531674 0.6421193 0.72444958 0.76996436
#                            Comp.6    Comp.7    Comp.8     Comp.9    Comp.10
# Standard deviation     0.96024608 0.8664106 0.7974705 0.73874672 0.64972015
# Proportion of Variance 0.03841969 0.0312778 0.0264983 0.02273945 0.01758901
# Cumulative Proportion  0.80838405 0.8396619 0.8661602 0.88889960 0.90648861
#                          Comp.11    Comp.12    Comp.13    Comp.14     Comp.15
# Standard deviation     0.6447846 0.59672323 0.52411736 0.51157790 0.462237302
# Proportion of Variance 0.0173228 0.01483661 0.01144579 0.01090466 0.008902638
# Cumulative Proportion  0.9238114 0.93864802 0.95009381 0.96099847 0.969901113
#                            Comp.16     Comp.17     Comp.18     Comp.19
# Standard deviation     0.397367112 0.353792182 0.314359262 0.306487543
# Proportion of Variance 0.006579193 0.005215371 0.004117573 0.003913942
# Cumulative Proportion  0.976480306 0.981695677 0.985813250 0.989727192
#                            Comp.20    Comp.21   Comp.22     Comp.23
# Standard deviation     0.276777892 0.26807447 0.2185241 0.164643192
# Proportion of Variance 0.003191917 0.00299433 0.0019897 0.001129474
# Cumulative Proportion  0.992919109 0.99591344 0.9979031 0.999032613
#                             Comp.24
# Standard deviation     0.1523721796
# Proportion of Variance 0.0009673867
# Cumulative Proportion  1.0000000000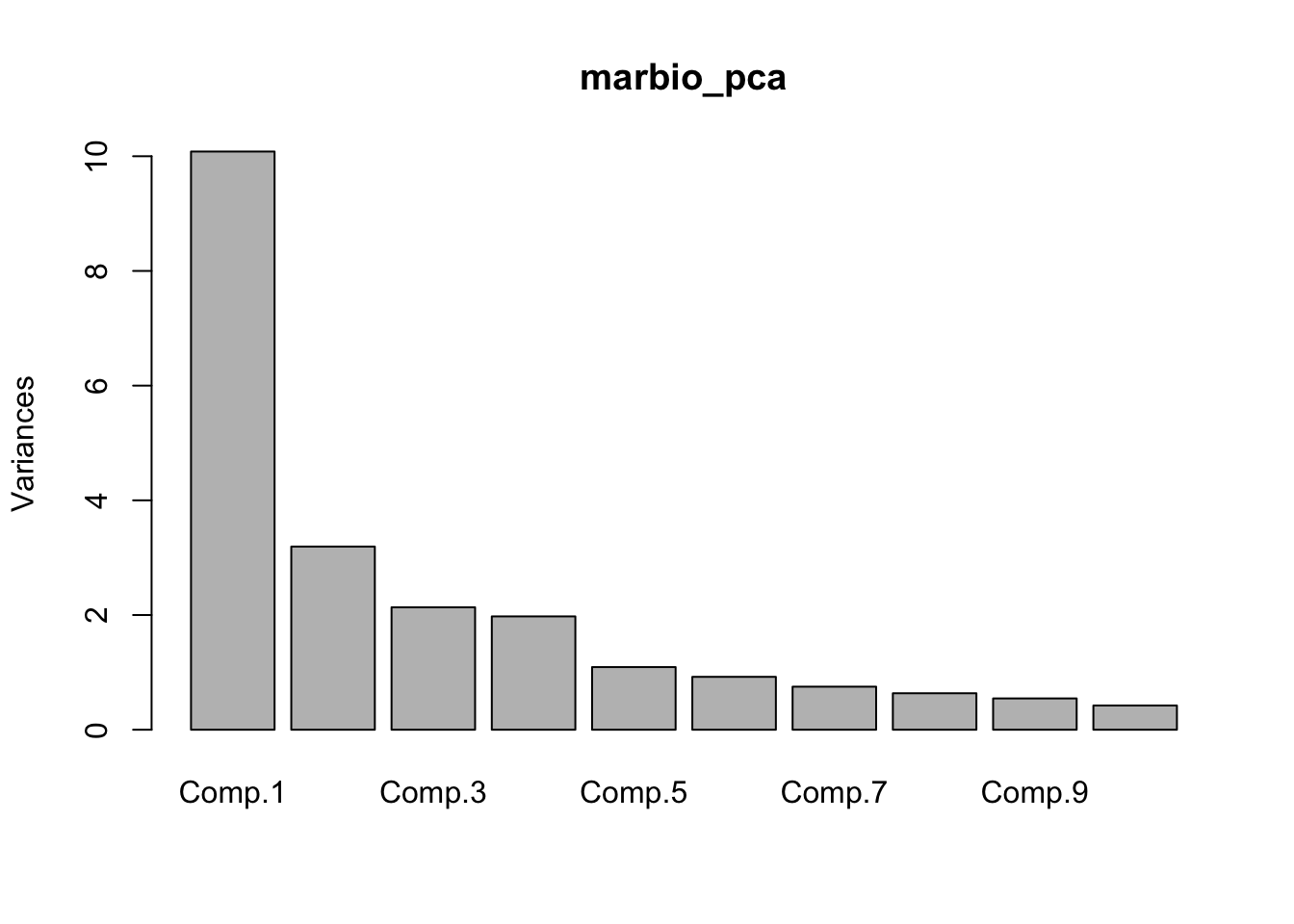

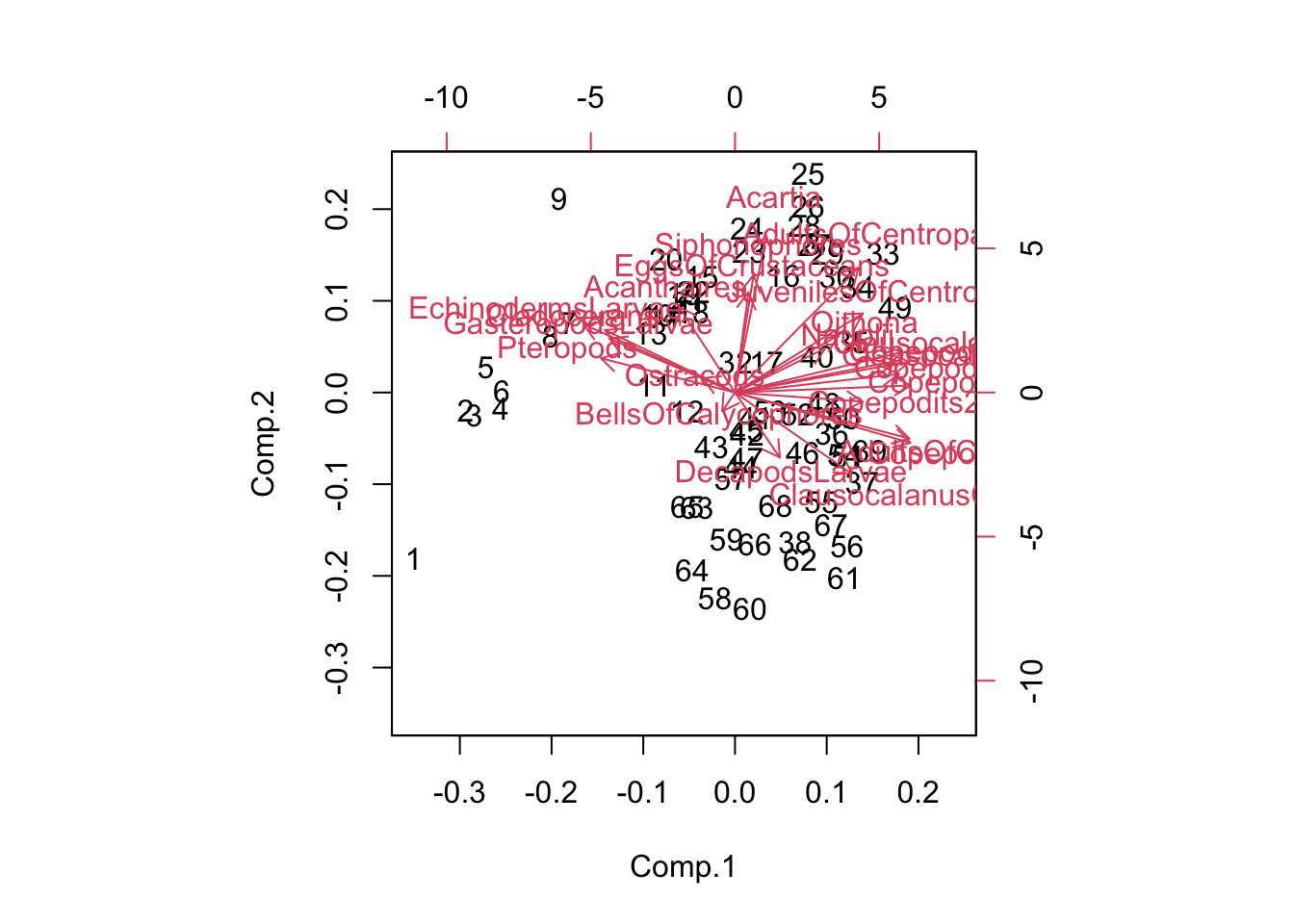
plot(marbio_pca) # Notez le graphique produit ici...

biplot(marbio_pca)

Pour effectuer une classification d’un sous-ensemble de marbio, vous pouvez utiliser :

 mb_log <- t(log(marbio[1:10, 1:10] + 1))
marbio_dist <- dist(mb_log, "eucl") # Matrice de distance
h <- hclust(marbio_dist, "average") # Classification
plot(h, hang = -1) # Notez le graphique produit ici!
rect.hclust(h, k = 3)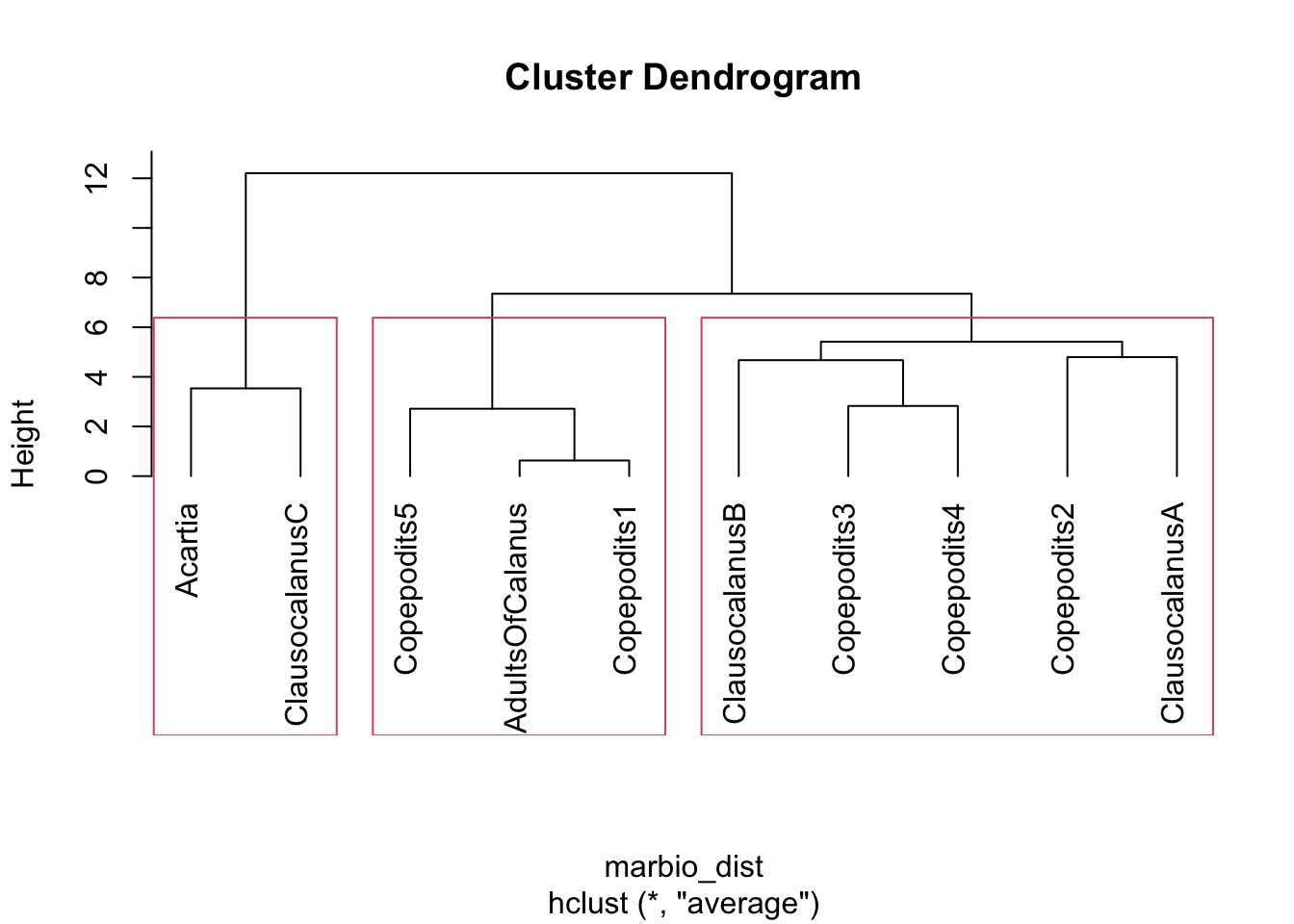

Au chapitre des avantages de l’organisation des analyses dans R, signalons notamment que le logiciel est à même d’interpréter au mieux des commandes telles que summary(), plot(), hist(), predict()… Par exemple, dans les deux traitements précédents, la même fonction plot() a des effets radicalement différents selon qu’elle est appliquée au résultat d’un ACP (cas 1) ou d’une classification (cas 2). Dans le premier cas, cette fonction a tracé ce que l’on appelle le graphique des éboulis des valeurs propres de l’ACP qui permet de déterminer le nombre d’axes que l’on devrait conserver. Dans le second cas, la même fonction a tracé un dendrogramme, c’est-à-dire, la meilleure représentation graphique pour une classification. Comment R a-t-il pu déterminer tout seul quel type de graphe choisir ? En fait, ceci est une conséquence de son organisation objet. Les deux analyses créent des objets différents, et chaque objet utilise sa propre version de la fonction plot(), version la plus adaptée dans son contexte. De telles fonctions qui réalisent des traitements différents selon l’objet considéré sont dites méthodes de l’objet. Même si les puristes diront qu’il ne s’agit pas à 100% d’une organisation objet, R par le biais de ses objets et méthodes, offre une organisation de type objet. Et cette organisation est à la fois très puissante et très souple.

A.4.5 Scripts et fonctions personnalisées

Comme nous venons de le voir au chapitre précédent, la moindre analyse nécessite de nombreuses commandes et il est vite usant de les rentrer dans la console R. Le mode de travail interactif à la console est très utile pour expérimenter différentes choses, mais son principal défaut est de ne permettre de rentrer qu’une seule commande à la fois. R peut heureusement également interpréter des scripts, qui contiennent eux, plusieurs commandes successives rassemblées dans un même fichier.

La façon la plus simple pour créer un script qui contient toutes les commandes du chapitre précédent est de sauver et d’ouvrir ensuite l’historique des commandes dans un éditeur de texte. Vous pouvez forcer la sauvegarde de l’historique des commandes sans nécessairement quitter R à l’aide de savehistory().
Lancez maintenant votre éditeur de texte préféré et ouvrez votre fichier .Rhistory qui se trouve dans le répertoire courant de R. Supprimez toutes les lignes qui ne correspondent pas au chapitre précédent et enregistrez votre fichier modifié (prenez l’habitude d’utiliser l’extension .R pour reconnaître vos scripts R d’autres fichiers sur le disque dur).
Maintenant, revenez à R et exécutez-y votre script à l’aide d’une instruction de type source("c:/temp/myscript.R") (adaptez bien entendu en fonction de votre fichier script) ou sous Windows, via le menu File -> Source R code.... Vous pouvez modifier votre script dans l’éditeur de texte qui est toujours ouvert, le resauver et le réexécuter dans R autant de fois que vous voulez, et donc le retravailler et tester la version modifiée par ce biais.
Avant d’en terminer avec l’édition de code, je voudrais vous montrer comme il est facile de créer des fonctions personnalisées dans R. Entrez le code suivant dans la console R cube <- function(x) {x^3} puis cube(1:3). Et oui, vous venez de créer une nouvelle fonction qui s’appelle cube() et qui élève un vecteur ou une matrice à la puissance 3. Quoique cette fonction soit très simple, la création d’une fonction personnalisée, même complexe, se fait toujours de cette façon dans R. Bien sûr, vous créerez plutôt vos fonctions complexes dans un fichier de code à extension .R que vous éditerez comme nous venons de le voir pour notre script. L’étape suivante est de créer un package pour redistribuer votre œuvre. Cela nécessite bien entendu quelques étapes supplémentaires (création de l’aide en ligne et des exemples, compilation du package…), mais rien de très compliqué.
Enfin pour clore ce chapitre, je voudrais vous signaler que le code de toutes les fonctions de R est disponible en clair dans l’environnement et peut être utilisé librement comme base pour vos fonctions personnalisées. Entrez par exemple cube(), puis log() et enfin ls() (soit le nom de fonctions, mais sans entrer les parenthèses et les arguments). Le code des fonctions correspondantes est imprimé dans la console. Vous reconnaîtrez le code de votre fonction personnalisée cube(). La fonction log(), pour des raisons de performance, fait appel à une fonction interne écrite en C (.Internal(...)). La fonction ls() est un peu plus complexe, comme vous pouvez le voir. Les fonctions existantes sont une excellente source d’inspiration pour apprendre à programmer correctement vos propres fonctions personnalisées dans R !