4.3 Manipulation et description
Tout comme pour les statistiques plus classiques, nous commençons toujours notre exploration de séries chronologiques par une partie purement descriptive, soit numérique, soit graphique. De plus, nous savons que nous ne devons pas espérer obtenir d’emblée des données qui se présentent de manière parfaite. Un petit peu de manipulation de données est parfois nécessaire… Nous allons découvrir quelques fonctions utiles dans ce contexte pour les séries chronologiques.
Comme nous l’avons déjà vu, le graphe de base (obtenu par plot() ou en utilisant geom_line()) est une ligne brisée qui relie les différents points de la série, avec le temps sur l’axe des abscisses, et l’axe des ordonnées représentant les observations de la variable quantitative mesurée au fil du temps.
4.3.1 Statistiques glissantes
Les descripteurs statistiques tels que la moyenne, la médiane, l’écart type, etc., restent utiles pour les séries temporelles. Par contre, la valeur de ces descripteurs est susceptible de varier au cours du temps, et cette variation donne des indications utiles sur les mécanismes biologiques sous-jacents (par exemple, des fluctuations, des changements brutaux de régimes, etc.). Il nous faut donc calculer ces descripteurs pour des intervalles de temps précis le long de l’axe temporel de notre série. Les statistiques glissantes (sliding statistics en anglais) correspondent précisément à l’analyse de blocs successifs de données suivant un axe spatio-temporel. Dans {pastecs}, elles se calculent à l’aide de la fonction stat.slide().
Exemple
Nous reprenons ici l’exemple du manuel de {pastecs}. On peut calculer des statistiques glissantes pour la série ClausocalanusA de marbio par groupes de dix stations, les imprimer et faire un graphique de la “moyenne glissante” à l’aide des instructions suivantes :
marbio_ts <- ts(read("marbio", package = "pastecs"))
statsl <- stat.slide(1:68, marbio_ts[, "ClausocalanusA"],
xmin = 0, n = 7, deltat = 10)
statsl# [0,10[ [10,20[ [20,30[ [30,40[ [40,50[ [50,60[ [60,70[
# xmin 0.000000 10.0000 20.0000 30.0000 40.0000 50.000 60.0000
# xmax 10.000000 20.0000 30.0000 40.0000 50.0000 60.000 70.0000
# nbr.val 9.000000 10.0000 10.0000 10.0000 10.0000 10.000 9.0000
# nbr.null 2.000000 0.0000 0.0000 0.0000 0.0000 0.000 0.0000
# nbr.na 0.000000 0.0000 0.0000 0.0000 0.0000 0.000 0.0000
# min 0.000000 160.0000 158.0000 96.0000 136.0000 56.000 52.0000
# max 12.000000 832.0000 1980.0000 1204.0000 2484.0000 824.000 656.0000
# median 4.000000 344.0000 732.0000 752.0000 260.0000 340.000 120.0000
# mean 4.777778 350.8000 810.1000 682.0000 494.4000 364.800 219.1111
# std.dev 4.790036 196.9708 619.8578 350.0616 711.0511 234.915 202.4231plot(statsl, stat = "mean", leg = TRUE, lpos = c(55, 2500),
xlab = "Station", ylab = "ClausocalanusA")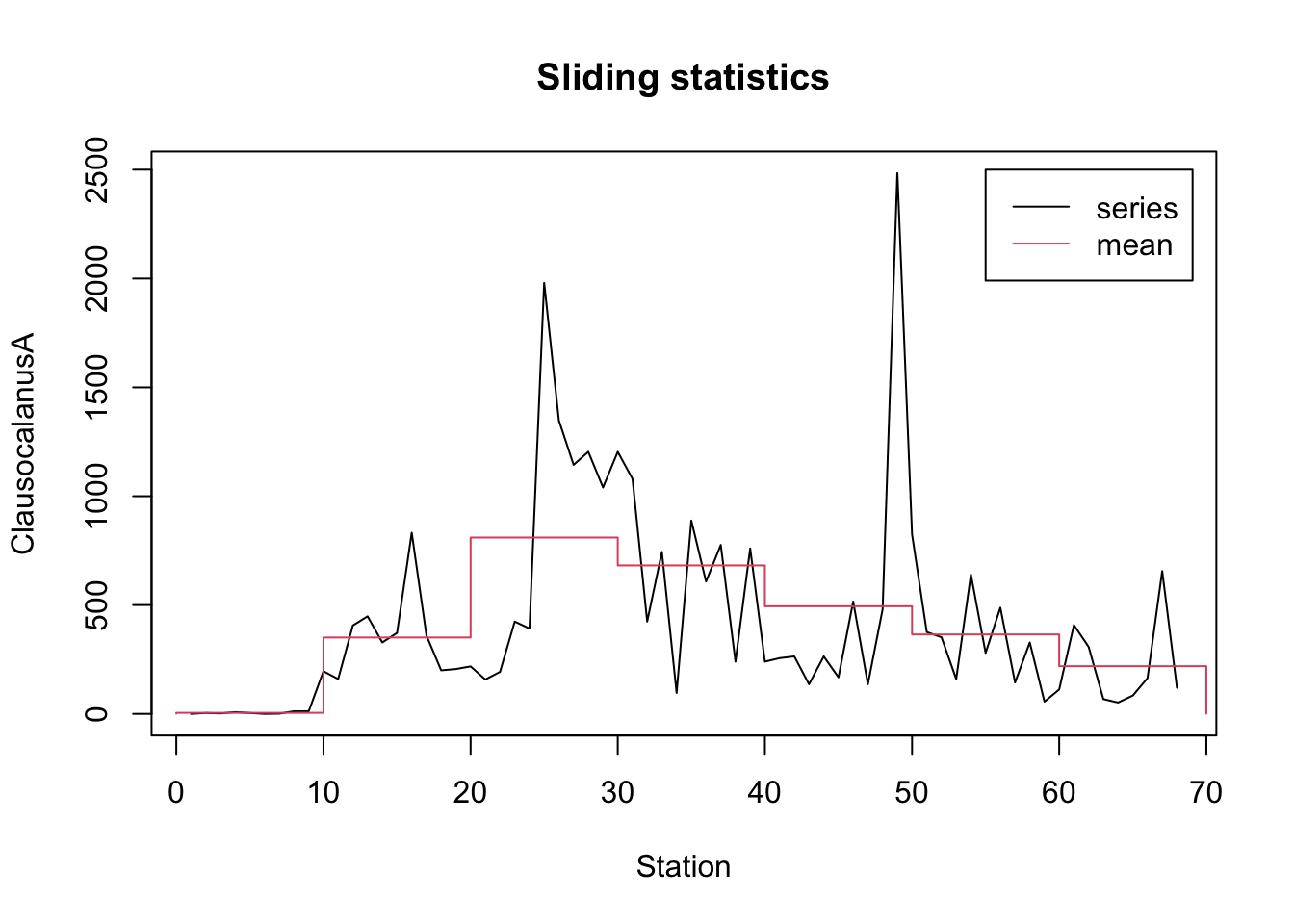
Toujours pour la même série, on peut calculer toutes les statistiques sur des intervalles irréguliers, puis représenter l’étendue (minimum, maximum) et la médiane pour chaque intervalle comme suit (ces intervalles correspondent aux différentes masses d’eaux croisées le long du transect, voir légende du graphique) :
statsl2 <- stat.slide(1:68, marbio_ts[, "ClausocalanusA"],
xcut = c(0, 17, 25, 30, 41, 46, 70),
basic = TRUE, desc = TRUE, norm = TRUE, pen = TRUE, p = 0.95)
statsl2# [0,17[ [17,25[ [25,30[ [30,41[
# xmin 0.000000e+00 1.700000e+01 2.500000e+01 3.000000e+01
# xmax 1.700000e+01 2.500000e+01 3.000000e+01 4.100000e+01
# nbr.val 1.600000e+01 8.000000e+00 5.000000e+00 1.100000e+01
# nbr.null 2.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
# nbr.na 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
# min 0.000000e+00 1.580000e+02 1.040000e+03 9.600000e+01
# max 8.320000e+02 4.240000e+02 1.980000e+03 1.204000e+03
# range 8.320000e+02 2.660000e+02 9.400000e+02 1.108000e+03
# sum 2.785000e+03 2.151000e+03 6.716000e+03 7.060000e+03
# median 1.200000e+01 2.120000e+02 1.204000e+03 7.440000e+02
# mean 1.740625e+02 2.688750e+02 1.343200e+03 6.418182e+02
# SE.mean 6.066894e+01 3.704796e+01 1.668120e+02 1.078927e+02
# CI.mean.0.95 1.293128e+02 8.760450e+01 4.631443e+02 2.403999e+02
# var 5.889153e+04 1.098041e+04 1.391312e+05 1.280492e+05
# std.dev 2.426758e+02 1.047875e+02 3.730029e+02 3.578396e+02
# coef.var 1.394188e+00 3.897255e-01 2.776973e-01 5.575404e-01
# skewness 1.248551e+00 4.181831e-01 8.469063e-01 -4.141160e-02
# skew.2SE 1.106268e+00 2.780098e-01 4.638697e-01 -3.133978e-02
# kurtosis 7.020336e-01 -1.852389e+00 -1.193537e+00 -1.424298e+00
# kurt.2SE 3.218053e-01 -6.254351e-01 -2.983842e-01 -5.566203e-01
# normtest.W 7.557989e-01 8.300443e-01 8.162687e-01 9.560890e-01
# normtest.p 7.467713e-04 5.943034e-02 1.092399e-01 7.221457e-01
# pos.median 8.600000e+01 2.120000e+02 1.204000e+03 7.440000e+02
# pos.mean 1.989286e+02 2.688750e+02 1.343200e+03 6.418182e+02
# geo.mean 3.935062e+01 2.522408e+02 1.307640e+03 5.181136e+02
# pen.mean 3.351203e+02 2.683489e+02 1.340628e+03 6.787440e+02
# pen.var 1.907110e+06 1.039770e+04 1.119418e+05 3.111941e+05
# pen.std.dev 1.380981e+03 1.019691e+02 3.345771e+02 5.578477e+02
# pen.mean.var 5.558396e+04 1.298434e+03 2.238628e+04 2.768567e+04
# [41,46[ [46,70[
# xmin 41.0000000 4.600000e+01
# xmax 46.0000000 7.000000e+01
# nbr.val 5.0000000 2.300000e+01
# nbr.null 0.0000000 0.000000e+00
# nbr.na 0.0000000 0.000000e+00
# min 136.0000000 5.200000e+01
# max 264.0000000 2.484000e+03
# range 128.0000000 2.432000e+03
# sum 1088.0000000 9.236000e+03
# median 256.0000000 3.080000e+02
# mean 217.6000000 4.015652e+02
# SE.mean 27.2939554 1.048611e+02
# CI.mean.0.95 75.7801688 2.174685e+02
# var 3724.8000000 2.529043e+05
# std.dev 61.0311396 5.028960e+02
# coef.var 0.2804740 1.252339e+00
# skewness -0.3597825 3.033043e+00
# skew.2SE -0.1970610 3.150646e+00
# kurtosis -2.1086492 9.865540e+00
# kurt.2SE -0.5271623 5.277023e+00
# normtest.W 0.7864078 6.024972e-01
# normtest.p 0.0625007 9.610838e-07
# pos.median 256.0000000 3.080000e+02
# pos.mean 217.6000000 4.015652e+02
# geo.mean 209.9226025 2.527195e+02
# pen.mean 218.0553885 3.905421e+02
# pen.var 4518.0257036 1.913652e+05
# pen.std.dev 67.2162607 4.374531e+02
# pen.mean.var 903.3938793 7.745030e+03plot(statsl2, stat = "median", xlab = "Stations", ylab = "Effectifs",
main = "Clausocalanus A") # Médiane
lines(statsl2, stat = "min") # Minimum
lines(statsl2, stat = "max") # Maximum
lines(c(17, 17), c(-50,2600), col = 4, lty = 2) # Séparations des masses d'eaux
lines(c(25, 25), c(-50,2600), col = 4, lty = 2)
lines(c(30, 30), c(-50,2600), col = 4, lty = 2)
lines(c(41, 41), c(-50,2600), col = 4, lty = 2)
lines(c(46, 46), c(-50,2600), col = 4, lty = 2)
text(c(8.4, 21, 27.5, 35, 43.5, 57.2), 2300,
labels = c("Zone périphérique", "D1", "C", "Front", "D2", "Zone centrale")) # Labels
legend(0, 1900, c("série", "médian", "étendue"), col = 1:3, lty = 1)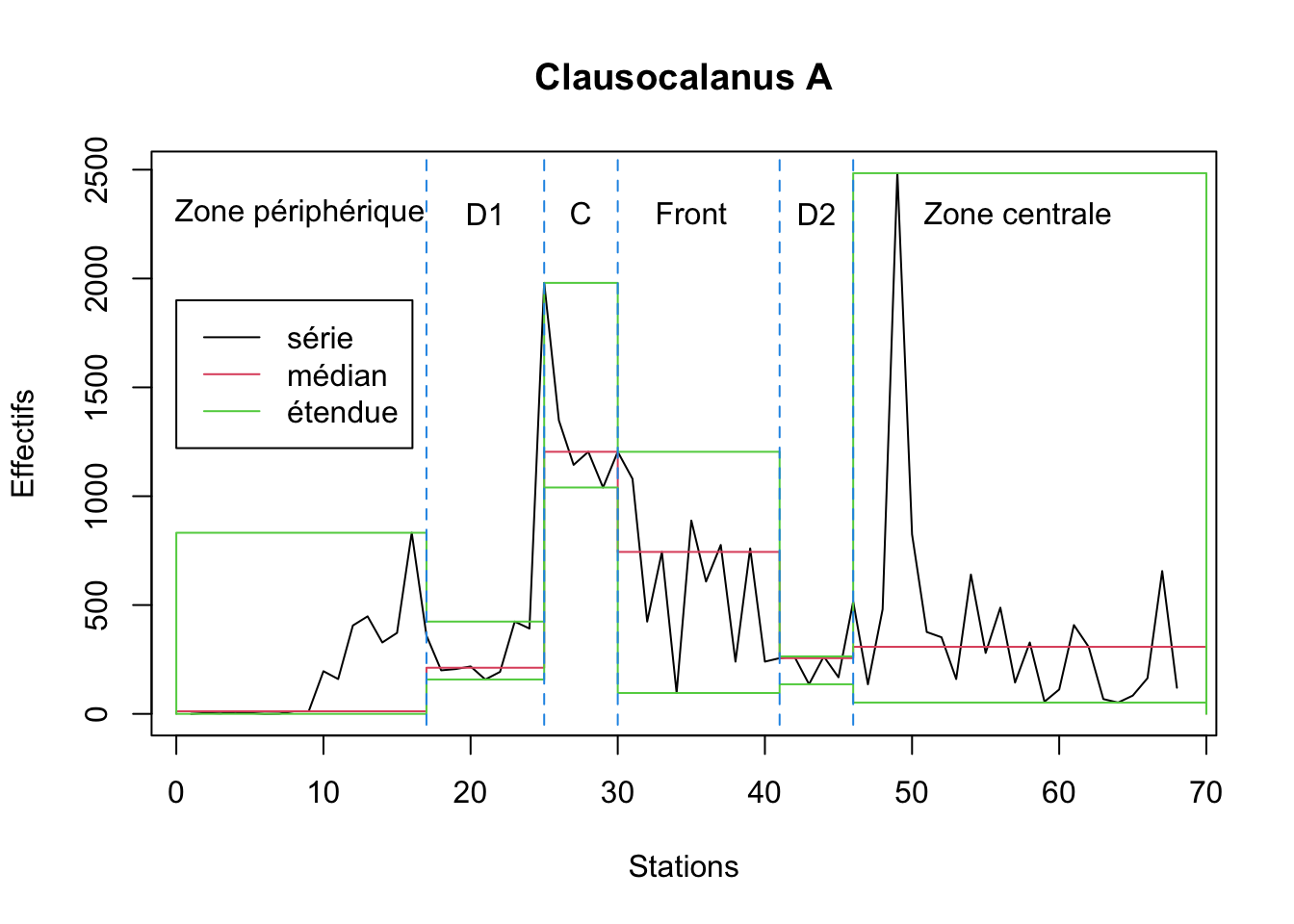
Enfin, on peut extraire différentes statistiques, les valeurs de la série initiale (y), les valeurs de temps de la série (x), et le vecteur temps de coupure des périodes (xcut) à partir de l’objet stat.slide renvoyé :
# [0,17[ [17,25[ [25,30[ [30,41[ [41,46[ [46,70[
# mean 174.0625 268.875 1343.2 641.8182 217.6 401.5652
# median 12.0000 212.000 1204.0 744.0000 256.0 308.0000
# min 0.0000 158.000 1040.0 96.0000 136.0 52.0000
# max 832.0000 424.000 1980.0 1204.0000 264.0 2484.0000# [1] 0 4 2 8 4 0 1 12 12 196 160 406 448 328 372
# [16] 832 360 200 206 218 158 193 424 392 1980 1348 1144 1204 1040 1204
# [31] 1080 424 744 96 888 608 776 240 760 240 256 264 136 264 168
# [46] 516 136 480 2484 824 376 352 160 640 280 488 144 328 56 112
# [61] 408 308 68 52 84 164 656 120# [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
# [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
# [51] 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68# [1] 0 17 25 30 41 46 70À vous de jouer !
Effectuez maintenant les exercices du tutoriel C04La_ts_intro (Introduction aux séries chronologiques).
BioDataScience3::run("C04La_ts_intro")4.3.2 Manipulations de ts
Les jeux de données bricolés artificiellement sont parfois bien utiles pour explorer de nouvelles techniques. En effet, puisque nous les construisons nous-mêmes, nous savons dès le départ de quoi ils sont faits. Et donc, nous pouvons vérifier que le résultat obtenu est bien conforme. Par exemple, nous pouvons construire une série de données mensuelle commençant en avril 1998 (start = c(1998, 4)), contenant 100 valeurs et comportant une composante sinusoïdale d’une période annuelle ainsi qu’une composante aléatoire ayant une distribution normale de moyenne nulle et d’écart type 0.5 :
# Jan Feb Mar Apr May Jun
# 1998 0.53423285 1.43327935 0.60420900
# 1999 -1.33370946 0.27857830 0.43481661 1.12420163 1.06515353 0.92922489
# 2000 -0.65564462 -0.97086485 0.34532497 0.54830940 0.60404433 1.08449282
# 2001 -1.34969680 -0.97706501 0.25585306 1.26164441 1.57201680 0.39920092
# 2002 -0.69639405 -0.15696210 -0.17617969 1.41003756 1.11029413 0.17552783
# 2003 -1.40083830 -0.70119835 -0.35667406 1.19120802 0.92628151 1.08972410
# 2004 -1.25290114 -0.61256468 -0.20620737 0.58739527 0.51965028 0.58456245
# 2005 -1.39782834 -0.78595359 0.55906818 1.50948675 0.56038849 0.20373670
# 2006 -0.77026956 -0.90798795 -0.22788183 0.20605194 0.12737210 0.78622903
# Jul Aug Sep Oct Nov Dec
# 1998 1.13572633 0.15098634 -0.12657466 -1.11625520 -0.83113961 -1.08296197
# 1999 0.53694950 0.82345622 0.63620226 0.44310440 -0.55727047 -1.01017934
# 2000 0.35666044 0.75512898 -0.29461618 -0.24869688 -0.94132383 -0.48331748
# 2001 1.30053614 0.20599610 0.31842482 -0.59240066 -0.56562973 -0.27407562
# 2002 0.56398249 0.75534006 0.27684597 -0.29780102 -0.45851357 -0.49077350
# 2003 0.12201815 0.24949023 -0.04246430 -1.01095191 0.02413909 -0.91693467
# 2004 0.65262714 1.39873117 -1.01819380 -0.69202925 -0.59681610 -1.09255020
# 2005 0.94346648 1.13833602 0.26022692 -0.67552049 -1.47445721 -1.04470059
# 2006 0.90429561Créons maintenant une série multiple en prenant notre série de départ, ainsi qu’une version décalée de cinq mois à l’aide de la fonction stats::lag() et représentons cela graphiquement :
mtser <- ts.intersect(tser, stats::lag(tser, 5))
plot(mtser, xlab = "Temps", main = "Série tser et série décalée de 5 mois")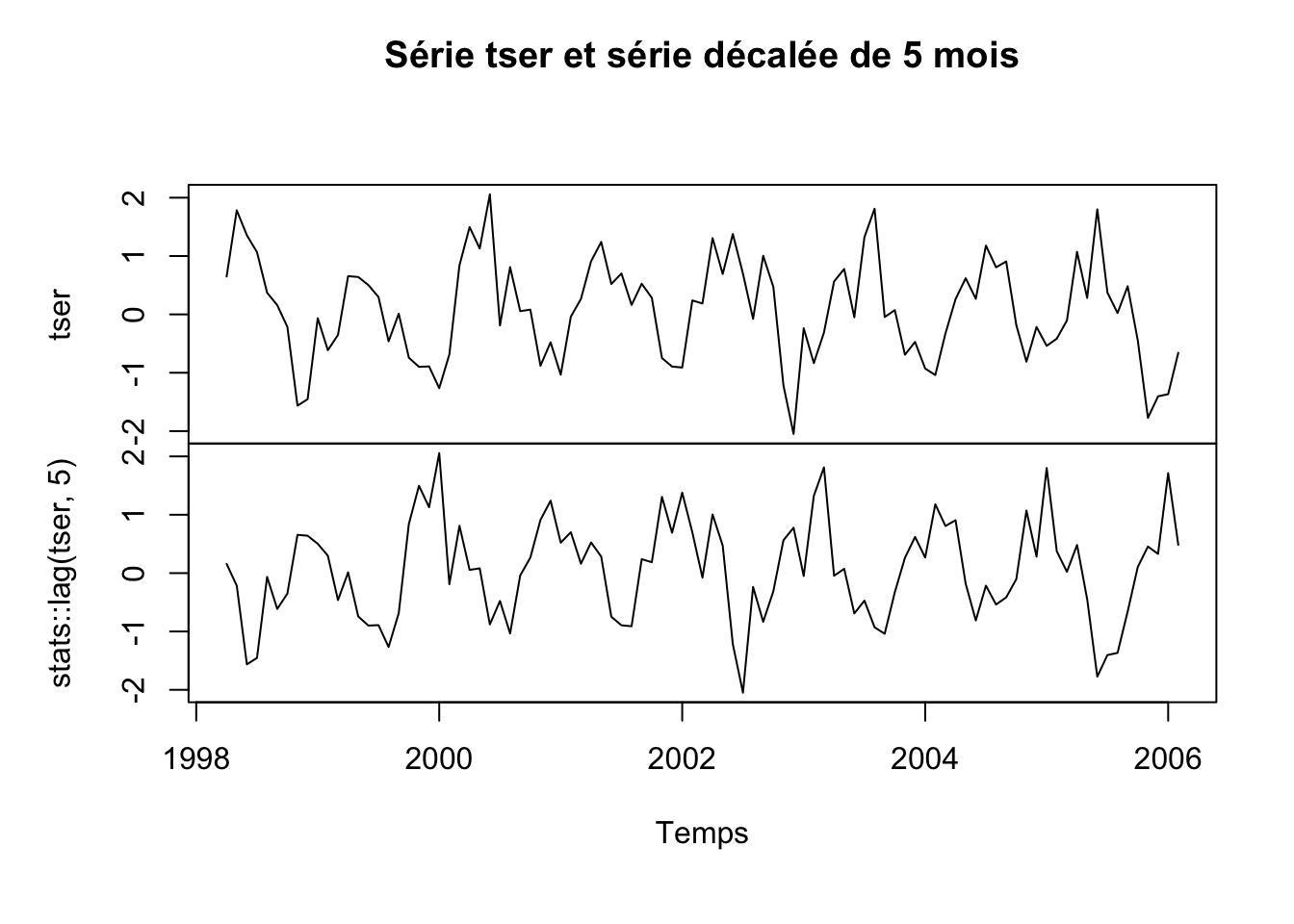
4.3.2.1 Manipulation du temps
Les fonctions tsp(), start(), end() et frequency() permettent de récupérer les différents paramètres de temps de la série :
# [1] 1998.25 2006.50 12.00# [1] 1998 4# [1] 2006 7# [1] 12Nous avons déjà vu la fonction time() qui permet de reconstituer le vecteur temps pour la série. La fonction cycle() indique l’appartenance de chaque donnée de la série à un cycle. Elle permet, par exemple, de séparer les données par mois si la base de temps est l’année à l’aide de la fonction split(). Ensuite, il est possible de traiter ou de représenter séparément les statistiques mois par mois pour en faire, par exemple, des boites de dispersions parallèles :
# Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
# 1998 4 5 6 7 8 9 10 11 12
# 1999 1 2 3 4 5 6 7 8 9 10 11 12
# 2000 1 2 3 4 5 6 7 8 9 10 11 12
# 2001 1 2 3 4 5 6 7 8 9 10 11 12
# 2002 1 2 3 4 5 6 7 8 9 10 11 12
# 2003 1 2 3 4 5 6 7 8 9 10 11 12
# 2004 1 2 3 4 5 6 7 8 9 10 11 12
# 2005 1 2 3 4 5 6 7 8 9 10 11 12
# 2006 1 2 3 4 5 6 7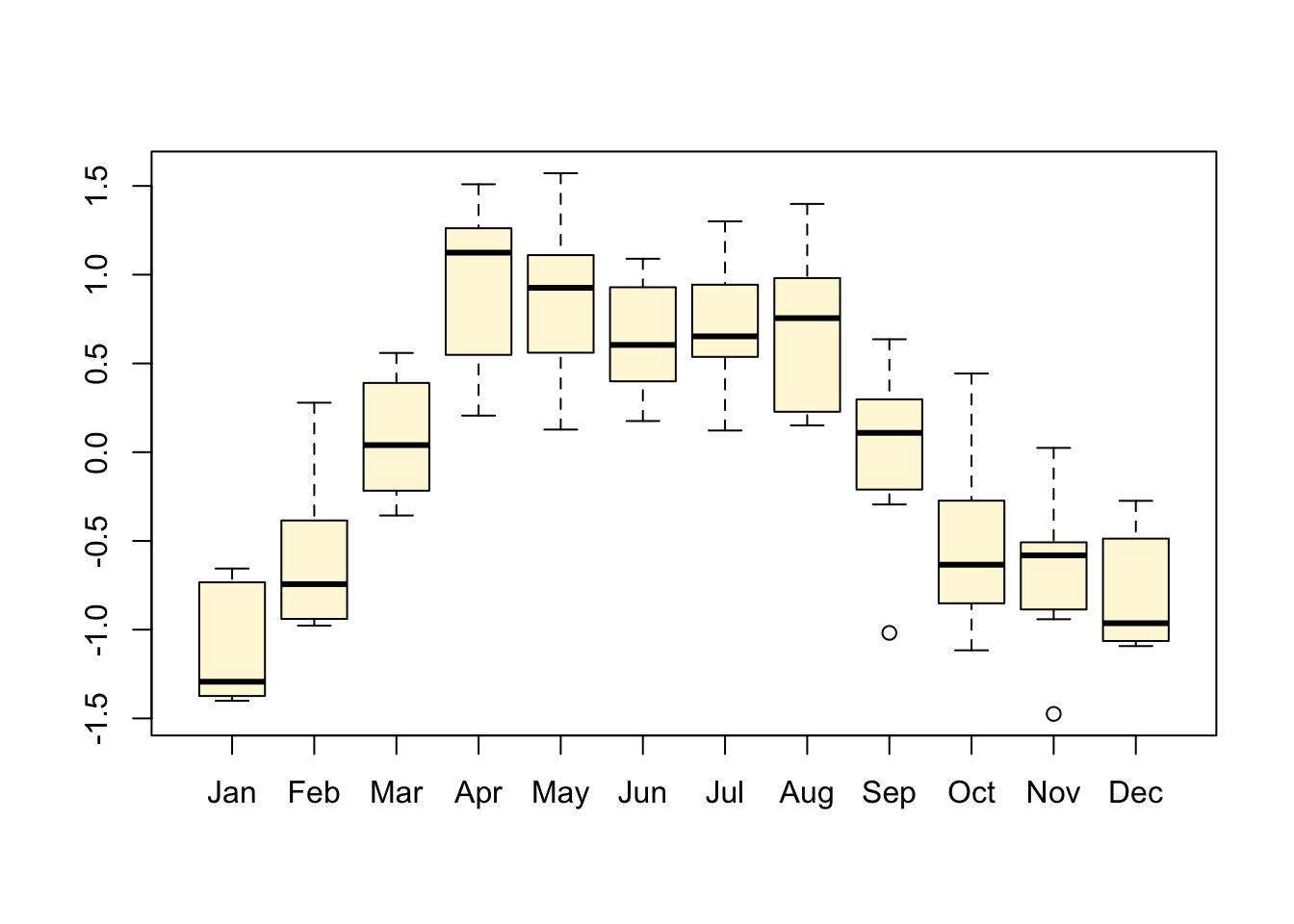
À vous de jouer !
Une autre manipulation courante de l’axe temporel consiste à agréger les données en des pas de temps plus longs. aggregate() permet de réduire le nombre d’observations en diminuant la fréquence. Par exemple pour transformer la série tser qui a un pas de temps d’un mois en une série de pas de temps d’un trimestre, en calculant des moyennes trimestrielles, nous ferons (puisqu’il y a quatre trimestres dans une année, nous indiquons 4 ici) :
# Qtr1 Qtr2 Qtr3 Qtr4
# 1998 0.8572404 0.3867127 -1.0101189
# 1999 -0.2067715 1.0395267 0.6655360 -0.3747818
# 2000 -0.4270615 0.7456155 0.2723911 -0.5577794
# 2001 -0.6903029 1.0776207 0.6083190 -0.4773687
# 2002 -0.3431786 0.8986198 0.5320562 -0.4156960
# 2003 -0.8195702 1.0690712 0.1096814 -0.6345825
# 2004 -0.6905577 0.5638693 0.3443882 -0.7937985
# 2005 -0.5415712 0.7578706 0.7806765 -1.0648928
# 2006 -0.6353798 0.3732177Notez encore une fois que R assume que l’unité de temps est l’année et il crée des intitulés particuliers pour des séries de fréquence égale à 4 (Qtr1 -> Qtr4) ou à 12 (intitulé des mois en abrégé).
Si nous ne souhaitons pas utiliser la série sur toute sa longueur, nous pouvons employer window() pour extraire une sous-série contenue dans une fenêtre de temps spécifique sans modifier la fréquence des observations. Par exemple, pour extraire les années 1999 à 2001 complètes de tser, on utilisera :
# Jan Feb Mar Apr May Jun
# 1999 -1.3337095 0.2785783 0.4348166 1.1242016 1.0651535 0.9292249
# 2000 -0.6556446 -0.9708649 0.3453250 0.5483094 0.6040443 1.0844928
# 2001 -1.3496968 -0.9770650 0.2558531 1.2616444 1.5720168 0.3992009
# Jul Aug Sep Oct Nov Dec
# 1999 0.5369495 0.8234562 0.6362023 0.4431044 -0.5572705 -1.0101793
# 2000 0.3566604 0.7551290 -0.2946162 -0.2486969 -0.9413238 -0.4833175
# 2001 1.3005361 0.2059961 0.3184248 -0.5924007 -0.5656297 -0.2740756La fonction stats::lag() permet de décaler la série en arrière dans le temps (ou en avant si on fournit une valeur de décalage négative) ; nous l’avons déjà utilisée plus haut. La fonction diff() calcule la différence entre une série et elle-même décalée dans le temps de k observations. Les fonctions ts.intersect() et ts.union() permettent de réunir deux ou plusieurs séries au sein d’une même matrice multivariée, avec une échelle de temps commune. Les fréquences respectives des séries à assembler doivent être identiques. Là où ts.intersect() retient uniquement l’intervalle de temps commun à toutes les séries, ts.union() conservera l’ensemble de l’intervalle temporel, toutes séries confondues.
Exercez-vous !
Manipulez et décrivez les différentes séries en exemples. Notez par exemple que EEG est constituée de mesures effectuées à un rythme de 256 par seconde, mais que l’axe du temps reprend simplement les observations les unes après les autres (ou si vous préférez, une “unité” de temps de 1/256 sec et une fréquence de 1). Comment feriez-vous pour transformer cette série avec une unité de temps de la seconde ? Ou de la milliseconde ?