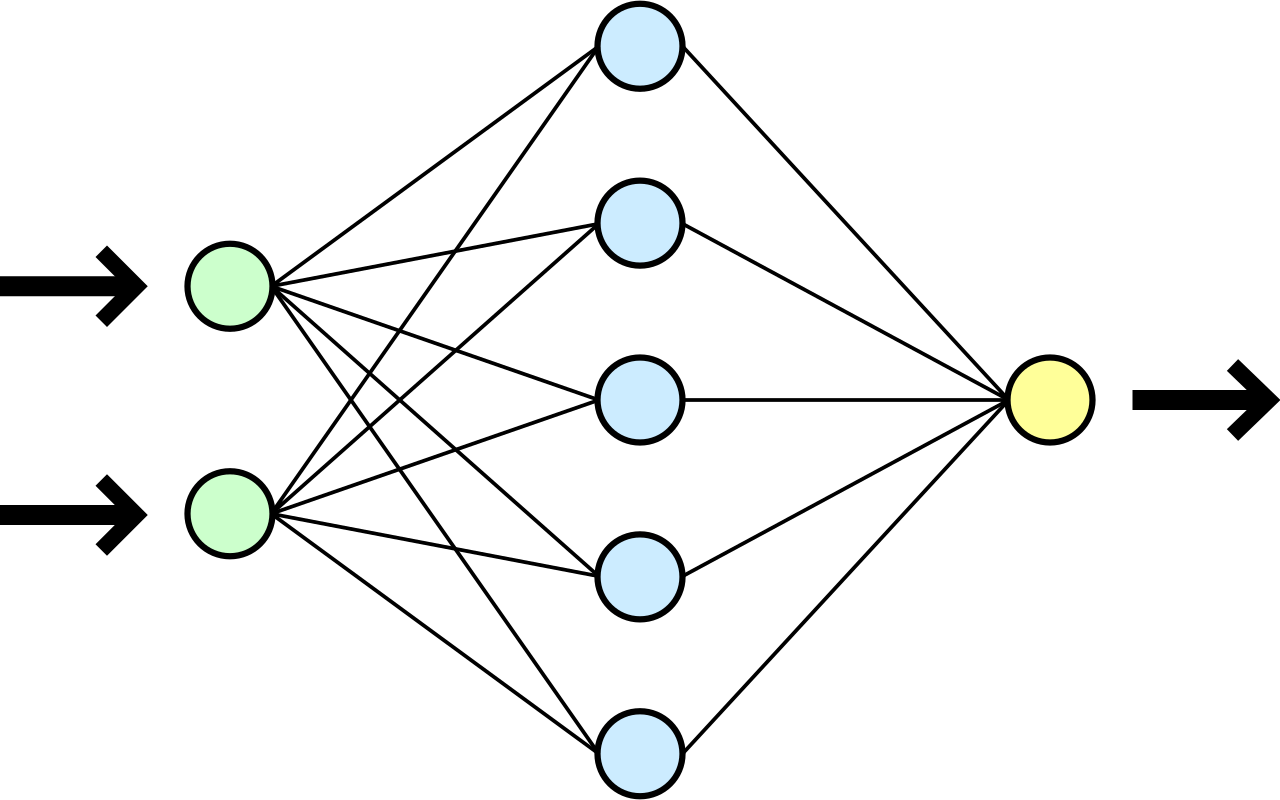
3.4 Réseaux de neurones artificiels

L’idée de cet algorithme vient de l’étude du fonctionnement de notre cerveau, d’où son nom, par analogie. Le modèle est constitué de plusieurs couches i interconnectées. Les nœuds j de ces connexions constituent les neurones artificiels. La première couche est constituée des attributs mesurés sur les individus et la dernière couche renseigne les classes à identifier (Venables & Ripley 2003). Là où les couches intermédiaires permettent de paramétrer le système d’apprentissage. Les connexions entre neurones sont caractérisées par les seuils ωij variants de 0 à 1, et le transfert du “signal” est, par exemple, modélisé par des fonctions logistiques variant entre ces deux extrêmes. Ces seuils permettent de moduler les relations entre neurones et ainsi de déterminer la classe à laquelle un individu appartient à partir des valeurs des attributs mesurés sur celui-ci, par la transmission des signaux de proche en proche, dont le passage est autorisé ou bloqué en fonction des seuils de déclenchement définis (Venables & Ripley 2003). Ce type de fonctionnement est, en effet, parfaitement comparable au transfert d’un influx nerveux le long d’un réseau de neurones dans notre cerveau.

Les réseaux de neurones artificiels sont des techniques très sophistiquées. Elles admettent potentiellement un grand nombre de paramètres différents (nombres de couches cachées, nombre de neurones par couche, fonction utilisée pour modéliser le signal, règle de définition des seuils…). Dans le cas de notre étude, nous utilisons un algorithme simple, dit à une seule couche cachée, et dont tous les autres paramètres sont conservés aux valeurs fournies par défaut dans le logiciel R. En pratique, il faudrait donc passer pas mal de temps sur l’optimisation d’un réseau de neurones pour en obtenir le meilleur.

Représentation simplifiée d’une partie d’un réseau de neurones à une seule couche cachée (en bleu) et complètement connectée. En vert, la couche sensorielle qui reçoit les valeurs des attributs. En jaune, le neurone qui prédit une classe (source Wikipedia).
Représentation simplifiée d’une partie d’un réseau de neurones à une seule couche cachée (en bleu) et complètement connectée. En vert, la couche sensorielle qui reçoit les valeurs des attributs. En jaune, le neurone qui prédit une classe (source Wikipedia).

3.4.1 Pima avec réseau de neurones

Un réseau de neurones simple à une seule couche cachée est disponible avec la fonction ml_nnet() dans {mlearning}. L’utilisation est similaire aux autres fonctions du package :

set.seed(85460)
pima1_nnet <- ml_nnet(data = pima1, diabetes ~ .)
# # weights:  11
# initial  value 271.909266 
# iter  10 value 245.725653
# iter  20 value 202.183190
# iter  30 value 176.514756
# iter  40 value 173.669481
# iter  50 value 169.294823
# iter  60 value 169.023133
# iter  70 value 168.702852
# final  value 168.701994 
# converged
pima1_nnet_conf <- confusion(cvpredict(pima1_nnet, cv.k = 10), pima1$diabetes)
# # weights:  11
# initial  value 243.559931 
# iter  10 value 223.356431
# iter  20 value 217.127240
# iter  30 value 216.667049
# iter  40 value 216.661542
# iter  50 value 216.661092
# final  value 216.660981 
# converged
# # weights:  11
# initial  value 243.607802 
# final  value 223.821228 
# converged
# # weights:  11
# initial  value 244.306611 
# final  value 224.224568 
# converged
# # weights:  11
# initial  value 244.003842 
# final  value 224.224569 
# converged
# # weights:  11
# initial  value 244.219063 
# final  value 224.224568 
# converged
# # weights:  11
# initial  value 244.874531 
# iter  10 value 223.733203
# iter  20 value 205.608100
# iter  30 value 197.765711
# iter  40 value 195.562416
# iter  50 value 194.236859
# iter  60 value 194.084248
# iter  70 value 194.084022
# iter  70 value 194.084021
# iter  70 value 194.084020
# final  value 194.084020 
# converged
# # weights:  11
# initial  value 243.981904 
# final  value 224.224568 
# converged
# # weights:  11
# initial  value 244.471374 
# final  value 224.224568 
# converged
# # weights:  11
# initial  value 245.072733 
# iter  10 value 209.219309
# iter  20 value 187.589856
# iter  30 value 183.436984
# iter  40 value 179.181280
# iter  50 value 168.809908
# iter  60 value 147.172433
# iter  70 value 146.217870
# iter  80 value 145.500888
# final  value 145.458053 
# converged
# # weights:  11
# initial  value 245.277015 
# iter  10 value 212.674626
# iter  20 value 193.540967
# iter  30 value 162.686700
# iter  40 value 160.919505
# iter  50 value 158.273718
# iter  60 value 156.384795
# iter  70 value 154.501711
# iter  80 value 154.339114
# iter  90 value 154.304936
# iter 100 value 154.278279
# iter 100 value 154.278278
# final  value 154.278278 
# converged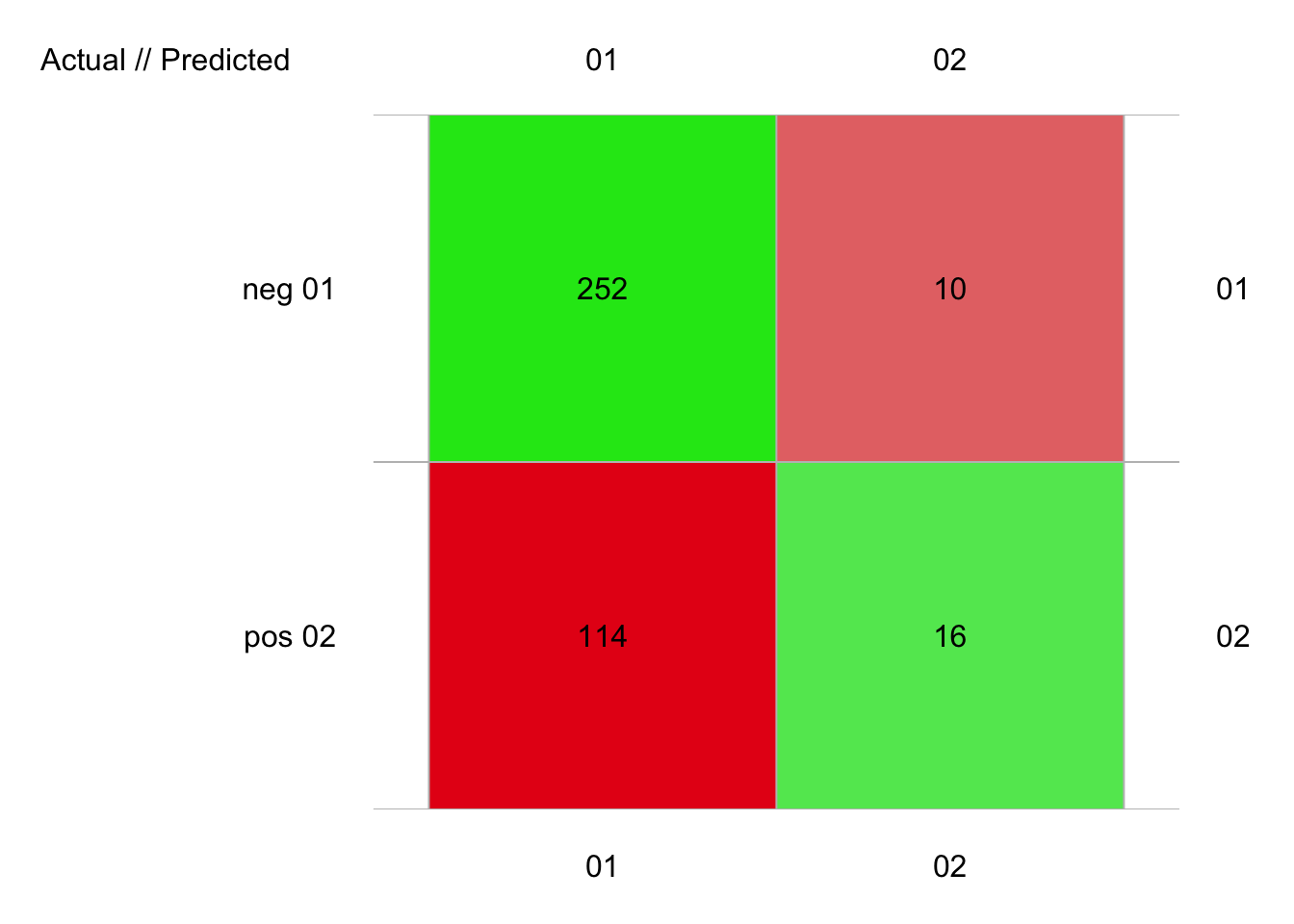
plot(pima1_nnet_conf)

summary(pima1_nnet_conf)
# 392 items classified with 268 true positives (error = 31.6%)
# 
# Global statistics on reweighted data:
# Error rate: 31.6%, F(micro-average): 0.592, F(macro-average): 0.504
# 
#        Fscore    Recall Precision Specificity       NPV        FPR        FNR
# neg 0.8025478 0.9618321 0.6885246   0.1230769 0.6153846 0.87692308 0.03816794
# pos 0.2051282 0.1230769 0.6153846   0.9618321 0.6885246 0.03816794 0.87692308
#           FDR       FOR     LRPT      LRNT     LRPS      LRNS    BalAcc
# neg 0.3114754 0.3846154 1.096826 0.3101145 1.790164 0.5061475 0.5424545
# pos 0.3846154 0.3114754 3.224615 0.9117216 1.975709 0.5586081 0.5424545
#           MCC    Chisq      Bray Auto Manu  A_M  TP  FP  FN  TN
# neg 0.1606382 10.11541 0.1326531  366  262  104 252 114  10  16
# pos 0.1606382 10.11541 0.1326531   26  130 -104  16  10 114 252

Avec les valeurs par défaut, notre réseau de neurones obtient des résultats décevants, avec un F micro de seulement 0.59 et un F macro de 0.50. Par contre, la fonction a beaucoup d’arguments qui représentent autant de paramètres à optimiser. Tout comme SVM, les réseaux de neurones nécessitent beaucoup de travail pour être optimisés correctement. De plus, il leur faut en général énormément de données en apprentissage avant d’avoir de bons résultats. Notre jeu de données pima1 avec ses 392 est un peu juste pour cet algorithme.

Une version plus évoluée du réseau de neurones, avec de très nombreuses couches a des propriétés nettement plus intéressantes qui en font l’un des outils les plus efficaces actuellement en apprentissage machine. Mais nous entrons ici dans le domaine de l’apprentissage profond…

Pour en savoir plus

  • Cette page présente les réseaux de neurones avec beaucoup de détails. En particulier, la vidéo “qu’est-ce qu’un réseau de neurones artificiels ?” est très claire, mais un peu longue malheureusement (près de 24min). En français.

3.4.2 Apprentissage profond

L’apprentissage profond (deep learning en anglais) est un domaine fascinant et plein d’avenir qui représente une forme moderne de réseaux de neurones exploitant la puissance de calcul des ordinateurs actuels. C’est un des piliers de l’intelligence artificielle. La vidéo suivante, bien qu’étant une publicité pour un acteur majeur du secteur (NVIDIA pour ne pas le nommer), est très bien faite pour comprendre les enjeux réels au-delà du buzz autour de l’intelligence artificielle et est même surprenante (mais vous devez la visionner pour comprendre pourquoi !)

Un réseau d’apprentissage profond est un très gros réseau de neurones contenant des centaines, des milliers, voire encore plus de neurones artificiels interconnectés en plusieurs couches. Il offre une telle plasticité au niveau de l’apprentissage qu’il est capable de s’adapter aux situations les plus complexes.

Cette animation montre bien les différentes étapes d’apprentissage d’un réseau profond par rapport à un problème simple en apparence seulement : la conduite autonome d’un véhicule.

Encore une autre vidéo qui montre comment un réseau profond a appris à marcher tout seul.

Malheureusement, l’apprentissage profond nécessite une quantité importante de calculs et tous les ordinateurs ne sont pas capables d’entraîner un tel modèle. Il faut généralement utiliser des processeurs GPU (donc des cartes graphiques puissantes) pour arriver à des vitesses d’apprentissage raisonnables. Nous allons donc nous limiter à un renvoi vers une petite démonstration simpliste juste pour vous illustrer la façon dont cela se passe.

Le jeu de données MNIST est un jeu de données ultra-classique et historique dans le développement de l’apprentissage profond. Il s’agit de plusieurs dizaines de milliers de chiffres manuscrits qui ont été numérisés. Le but est de créer un classifieur capable de reconnaître l’écriture manuscrite de nombres en reconnaissance, donc les chiffres de 0 à 9. La résolution de ce problème dans R est présentée ici. C’est un excellent point de départ si vous voulez vous lancer dans l’apprentissage profond. Dans le cadre de ce cours, nous n’irons cependant pas plus loin. Sachez toutefois que les meilleurs classifieurs en apprentissage profond sont actuellement capables de faire aussi bien, voire mieux dans la lecture de nombres en écriture manuscrite qu’un opérateur humain !

À vous de jouer !

Effectuez maintenant les exercices du tutoriel C03Lb_ml3 (SVM et réseaux de neurones).

BioDataScience3::run("C03Lb_ml3")

Complétez à présent votre projet individuel.

Réalisez le travail C03Ia_cardiovascular, partie II.

Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques III à l’UMONS à terminer avant le 2024-11-11 23:59:59.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md, partie II.

Vous devez aussi terminer le projet de groupe initié au module 1 (métriques) et continué au module 2 (optimisation).

Réalisez en groupe le travail C01Ga_metrics, partie III.

Travail en groupe de 4 pour les étudiants inscrits au cours de Science des Données Biologiques III à l’UMONS à terminer avant le 2024-11-26 23:59:59.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md, partie III.

Pour en savoir plus

Cette vidéo explique dans le détail le principe de fonctionnement d’un réseau profond et l’illustre justement sur l’apprentissage de la classification de chiffres manuscrits.