4.2 Modèle linéaire généralisé mixte

Dans le cours SDD I module 10 nous avons découvert les effets aléatoires dans les modèles comme étant une variable ayant une distribution statistique connue (souvent normale) dont on tire un échantillon aléatoire dans notre jeu de données. Cela se produit lorsque les modalités de la variable facteur utilisée sont très nombreuses et que seulement un petit nombre tiré au hasard est étudié. L’exemple que nous avions donné était le cas d’antibiotiques testés dans différentes boîtes de Pétri. Nous avions un nombre restreint et fixe d’antibiotiques, mais les boîtes de Pétri utilisées représentent en quelque sort un échantillon parmi la population statistique de boîtes de Pétri. De plus, l’effet “boîte de Pétri” n’est pas le sujet principal de l’étude. Comme nous suspections que la boîte de Pétri pouvait aussi avoir un impact sur le résultat, nous l’avons incluse dans notre modèle, mais comme effet aléatoire. Lorsque nous mélangeons un ou plusieurs effets aléatoires avec des effets fixes, nous obtenons alors un modèle linéaire mixte (LMM) ou un modèle linéaire généralisé mixte (GLMM) en fonction de la variable réponse \(y\) utilisée et la fonction de lien.

Prenons un exemple concret. Des scientifiques veulent mesurer l’effet d’une concentration croissante en éthanol dans le liquide séminal de l’homme sur la mobilité des spermatozoïdes. La question est évidemment en relation avec la consommation d’alcool et la fertilité, mais aussi avec des protocoles expérimentaux qui utilisent des molécules dissoutes dans l’éthanol. Des spermatozoïdes de huit patients différents sont soumis à des concentrations de 0, 0,1, 0,5, 1 et 2% d’éthanol pendant 4h. Ensuite, le nombre de spermatozoïdes mobiles est décompté sous microscope. Plutôt que d’encoder une variable binaire qui prend 1 si un spermatozoïde est mobile et 0 dans le cas contraire, un tableau plus compact qui reprend le nombre de spermatozoïdes mobiles et le total des spermatozoïdes comptés pour chaque échantillon des huit donneurs à chaque concentration d’éthanol. Voici les résultats obtenus :

spe <- dtbl_rows(
 ~donor, ~conc, ~mobile, ~total,
      1,   0.0,     236,    301,
      1,   0.1,     238,    301,
      1,   0.5,     115,    154,
      1,   1.0,     105,    196,
      1,   2.0,     182,    269,
      2,   0.0,      92,    150,
      2,   0.1,      60,    111,
      2,   0.5,      63,    131,
      2,   1.0,      46,     95,
      2,   2.0,      50,    125,
      3,   0.0,     100,    123,
      3,   0.1,      91,    117,
      3,   0.5,     132,    162,
      3,   1.0,     145,    187,
      3,   2.0,      52,     92,
      4,   0.0,      83,    113,
      4,   0.1,     104,    123,
      4,   0.5,      65,     87,
      4,   1.0,      93,    136,
      4,   2.0,      78,    117,
      5,   0.0,     127,    152,
      5,   0.1,      82,    114,
      5,   0.5,      55,     84,
      5,   1.0,      80,    103,
      5,   2.0,      98,    120,
      6,   0.0,      62,     77,
      6,   0.1,      65,     79,
      6,   0.5,      63,     72,
      6,   1.0,      57,     67,
      6,   2.0,      39,     66,
      7,   0.0,      91,    116,
      7,   0.1,      51,     71,
      7,   0.5,      70,     87,
      7,   1.0,      53,     72,
      7,   2.0,      59,     82,
      8,   0.0,     121,    137,
      8,   0.1,      80,     98,
      8,   0.5,     100,    122,
      8,   1.0,     126,    157,
      8,   2.0,      98,    122
)

Nous verrons une autre forme pour la formule que dans l’exemple Babies qui tient compte de ce type d’encodage. Il nous faut calculer la fraction des spermatozoïdes mobiles, et aussi nous assurer que la variable donor soit bien factor et que la variable conc soit numeric (nous voulons faire une régression de la fraction mobile en fonction de la concentration en éthanol) :

spe <- smutate(spe, mob_frac = mobile / total, donor = as.factor(donor), conc = as.numeric(conc))
head(spe)

# # A tibble: 6 × 5
#   donor  conc mobile total mob_frac
#   <fct> <dbl>  <dbl> <dbl>    <dbl>
# 1 1       0      236   301    0.784
# 2 1       0.1    238   301    0.791
# 3 1       0.5    115   154    0.747
# 4 1       1      105   196    0.536
# 5 1       2      182   269    0.677
# 6 2       0       92   150    0.613

La variable réponse est ici, en réalité, une variable binaire même si elle est encodée autrement. Pour chaque spermatozoïde observé, on peut avoir un résultat 0 (immobile) ou 1 (mobile), et la distribution peut être considérée comme une binomiale avec le nombre d’essais égal n égal à 1 (voir cours SDD I module 7). On parle aussi de distribution de Bernouilli dans le cas particulier d’une distribution binomiale à un seul essai. La mesure est répétée un nombre de fois spécifié dans notre tableau dans la colonne total pour chaque échantillon traité (8 donneurs x 5 concentrations d’éthanol = 40 échantillons). Donc, nous sommes dans une situation différente du jeu de données mite parce qu’il n’y a pas indépendance entre les observations pour chaque spermatozoïde. Plusieurs dizaines à centaines d’entre eux sont dénombrés à chaque fois dans le même échantillon. Les mesures répétées pour un même sujet d’expérience et lorsque le sujet de l’expérience est lui-même un facteur aléatoire sont automatiquement prises en compte correctement dans un modèle mixte.

À vous de jouer !

4.2.1 Ajustement et analyse d’un GLMM

Nous ne pouvons pas ajuster un modèle mixte avec la fonction glm(). Nous devons faire appel à une autre fonction : lme4::glmer(). Par contre, la syntaxe est la même : data = spécifie le jeu de données utilisé, une formule spécifie le modèle à ajuster, et family = indique la distribution de la variable réponse et aussi éventuellement la fonction de lien à utiliser. La formule encode un terme aléatoire entre parenthèse avec les facteurs fixes covariables suivis d’une barre verticale et le facteur aléatoire. Donc, par exemple, si nous considérons que la pente et l’ordonnée à l’origine des droites peuvent varier librement d’un donneur à l’autre, nous écrirons (conc | donor) pour le terme aléatoire. Si nous considérons que seule l’ordonnée à l’origine peut varier, mais pas la pente, nous écrirons (1 | donor), et enfin, si nous considérons que seule la pente, mais pas l’ordonnée à l’origine peut varier d’un donneur à l’autre, alors nous écrirons (0 + conc | donor). Ceci correspond aux différentes formes entre deux variables facteur dans le modèle classique (modèle complet f1 * f2 fixe -> f1 + (f1 | f2) en f2 aléatoire, modèle sans interactions f1 + f2 fixe -> f1 + (1 | f2), et modèle avec seulement les interactions pour le second facteur f1 + f1:f2 -> f1 + (0 + f1 | f2), respectivement).

À vous de jouer !

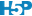
Nous devons encore comprendre comment indiquer dans la formule que nous n’avons pas une variable réponse binaire dans notre tableau, mais un contingentement des spermatozoïdes mobiles et du total. Cela s’indique par cbind(mobile, total - mobile), c’est-à-dire, un tableau à deux colonnes avec la première, le nombre observé de niveaux 1, et la seconde, le nombre observé de niveau 0 de la variable binaire. Avec ceci, nous pouvons à présent écrire la formule de notre modèle complet, le calculer et imprimer le résumé des résultats (malheureusement, nous ne pouvons pas encore utiliser tabularise() ici, car une méthode spécifique à ces objets n’a pas encore été écrite) :

spe_m1 <- lme4::glmer(data = spe, cbind(mobile, total - mobile) ~ conc + (conc | donor),
  family = binomial(link = "logit"))
summary(spe_m1)

# Generalized linear mixed model fit by maximum likelihood (Laplace
#   Approximation) [glmerMod]
#  Family: binomial  ( logit )
# Formula: cbind(mobile, total - mobile) ~ conc + (conc | donor)
#    Data: spe
# 
#      AIC      BIC   logLik deviance df.resid 
#    320.3    328.7   -155.1    310.3       35 
# 
# Scaled residuals: 
#     Min      1Q  Median      3Q     Max 
# -4.9916 -0.7375  0.0028  0.9353  1.8933 
# 
# Random effects:
#  Groups Name        Variance Std.Dev. Corr 
#  donor  (Intercept) 0.16977  0.4120        
#         conc        0.02106  0.1451   -0.02
# Number of obs: 40, groups:  donor, 8
# 
# Fixed effects:
#             Estimate Std. Error z value Pr(>|z|)    
# (Intercept)  1.26479    0.15390   8.219  < 2e-16 ***
# conc        -0.29582    0.06886  -4.296 1.74e-05 ***
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 
# Correlation of Fixed Effects:
#      (Intr)
# conc -0.163

La première ligne nous indique que le modèle n’est pas ajusté par régression par les moindres carrés des résidus, mais par une autre approche (maximum de vraisemblance, maximum likelihood en anglais). Un peu plus bas, nous observons un tableau qui donne le coefficient d’Akaike AIC, et d’autres statistiques générales sur le modèle ajusté. Ceci remplace le R² d’une régression linéaire qui n’a pas de sens ici. Ensuite, nous avons une idée de la distribution des résidus, et puis deux tableaux distincts nommés Random effects et Fixed effects. Les deux types d’effets doivent être traités différemment.

Pour les effets aléatoires, nous avons des distributions normales et les paramètres sont les variances liées à ces distributions. Pour l’ordonnée à l’origine, l’effet donneur se marque par une variance de 0.17, et pour la pente, la variance est de 0.021. Il n’y a pas de test de significativité de ces paramètres dans le résumé. Par contre, la corrélation entre ces paramètres est calculée et indiquée également (elle est très faible dans l’exemple).

Pour les effets fixes, nous retrouvons un tableau similaire à celui des coefficients dans le modèle linéaire classique, à ceci près que les tests t de Students pour la significativité des paramètres p (H₀: p = 0 et H₁: p ≠ 0) sont remplacés par des tests z considérant une distribution normale (comme pour une GLM). Ce test est une approximation et n’est pas aussi fiable dans le modèle mixte que dans le modèle classique. Nous pouvons néanmoins voir que l’ordonnée à l’origine ainsi que la pente en fonction de la concentration en éthanol sont tous deux significativement différentes de zéro au seuil \(\alpha\) de 5%. Comme la pente relative à conc est négative, nous pourrons considérer que l’effet moyen d’une augmentation d’éthanol dans le liquide séminal diminue la mobilité des spermatozoïdes.

L’avantage d’utiliser une formulation des variables avec le nombre de cas positifs, le total, et la fraction positive dans mob_frac est que nous pouvons ici réaliser une représentation graphique du modèle. Voici comment faire :

chart(data = spe, mob_frac ~ conc %col=% donor) +
  geom_point() +
  geom_line(f_aes(fitted(spe_m1) ~ conc %col=% donor)) +
  labs(x   = "Ethanol [%]",
       y   = "Mobilité des spermatozoïdes [%]",
       col = "Donneur")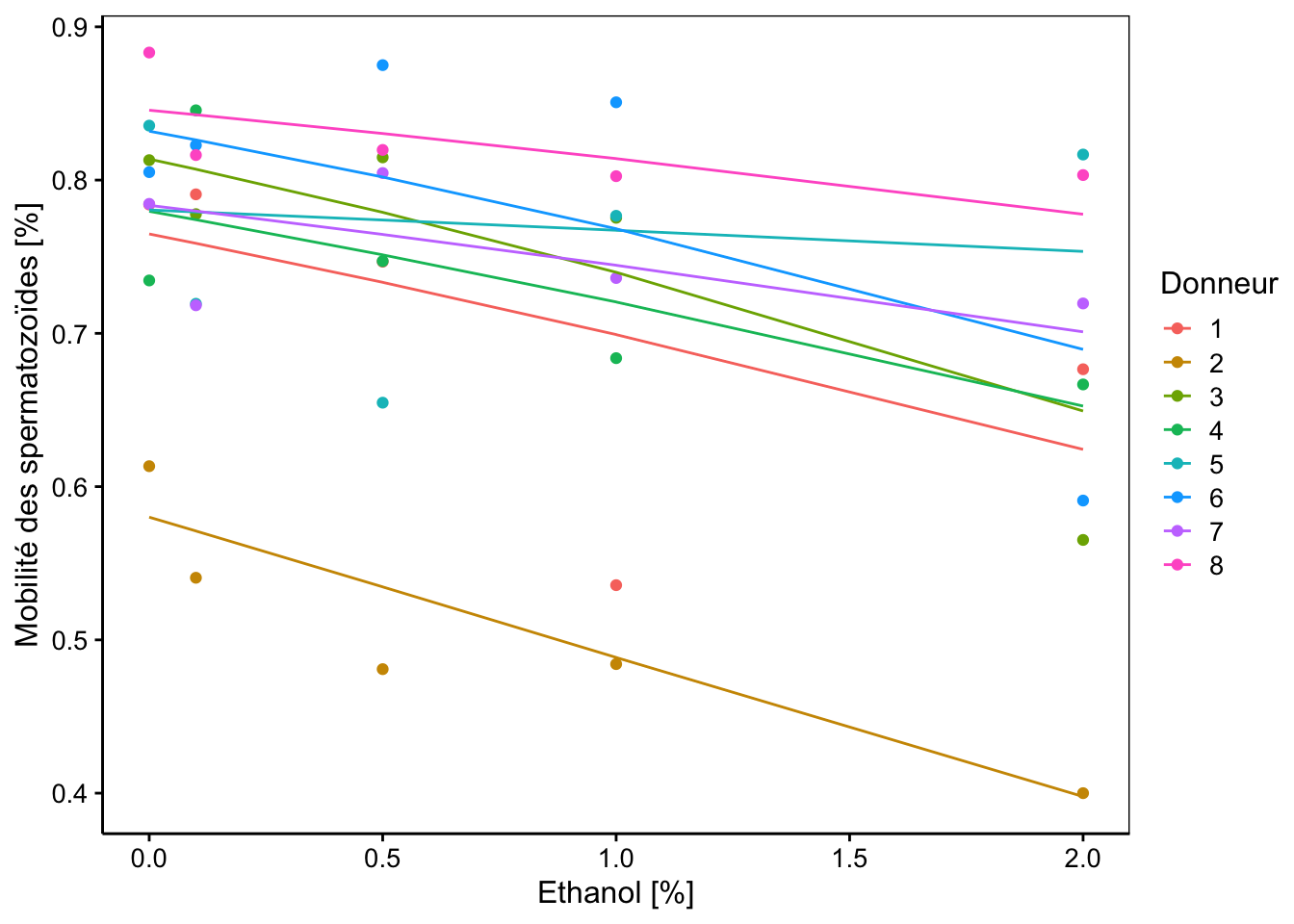

Nous observons effectivement des droites ajustées par le modèle qui ont toutes de pentes négatives, mais ces pentes sont modulées d’un donneur à l’autre, de même que leurs ordonnées à l’origine. Toutefois, la plupart de ces droites semblent avoir des pentes relativement parallèles. Nous pourrions nous demander s’il ne serait pas utile de simplifier notre modèle à ce niveau.

4.2.2 Simplification du modèle

Pour déterminer si nous pouvons simplifier un (G)LMM, nous pouvons utiliser anova() en comparant deux modèles imbriqués, spe_m1 notre modèle complet avec (conc | donor) et spe_m2 simplifié avec (1 | donor). La subtilité, c’est que comme ces modèles sont ajustés via le maximum de vraisemblance, ce n’est pas un test F de l’ANOVA qui est réalisé, mais un test de rapport de maximum de vraisemblance qui suit asymptotiquement une distribution du Chi². Pour le reste, l’interprétation reste la même. On a H₀: les deux modèles s’ajustent de manière identique, et H₁: le modèle plus complexe s’ajuste mieux que le plus simple. Donc, si on ne rejette pas H₀, nous concluons que le modèle le plus simple est aussi bon que le plus complexe et nous avons un argument fort en faveur de la simplification. Appliquons ceci directement :

spe_m2 <- lme4::glmer(data = spe,
  cbind(mobile, total - mobile) ~ conc + (1 | donor),
  family = binomial(link = "logit"))
anova(spe_m1, spe_m2)

# Data: spe
# Models:
# spe_m2: cbind(mobile, total - mobile) ~ conc + (1 | donor)
# spe_m1: cbind(mobile, total - mobile) ~ conc + (conc | donor)
#        npar    AIC    BIC  logLik deviance Chisq Df Pr(>Chisq)
# spe_m2    3 319.58 324.65 -156.79   313.58                    
# spe_m1    5 320.28 328.72 -155.14   310.28 3.302  2     0.1919

Nous ne rejetons pas H₀au seuil \(\alpha\) de 5%. Nous pouvons donc considérer les deux modèles comme expliquant de manière similaire les données et décider d’utiliser le modèle plus simple spe_m2. En voici le résumé :

summary(spe_m2)

# Generalized linear mixed model fit by maximum likelihood (Laplace
#   Approximation) [glmerMod]
#  Family: binomial  ( logit )
# Formula: cbind(mobile, total - mobile) ~ conc + (1 | donor)
#    Data: spe
# 
#      AIC      BIC   logLik deviance df.resid 
#    319.6    324.6   -156.8    313.6       37 
# 
# Scaled residuals: 
#     Min      1Q  Median      3Q     Max 
# -5.0521 -0.5711  0.0252  0.9661  2.8884 
# 
# Random effects:
#  Groups Name        Variance Std.Dev.
#  donor  (Intercept) 0.1794   0.4236  
# Number of obs: 40, groups:  donor, 8
# 
# Fixed effects:
#             Estimate Std. Error z value Pr(>|z|)    
# (Intercept)  1.26983    0.15723   8.076 6.69e-16 ***
# conc        -0.30297    0.04266  -7.103 1.22e-12 ***
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 
# Correlation of Fixed Effects:
#      (Intr)
# conc -0.209

Dans le tableau des effets aléatoires, nous n’avons plus qu’une seule variance estimée, celle correspondant à un décalage de l’ordonnée à l’origine par donneur, dont la variance vaut 0.18. Ce modèle signifie que nous considérons que la variation d’un donneur à l’autre se manifeste sous la forme d’un taux de mobilité spermatique initial (à concentration 0 en éthanol) différent d’une personne à l’autre. Par contre, le modèle considère aussi que l’effet de l’augmentation en éthanol est proportionnel à ce taux initial, quel que soit le donneur. Le graphique correspondant est le suivant :

chart(data = spe, mob_frac ~ conc %col=% donor) +
  geom_point() +
  geom_line(f_aes(fitted(spe_m2) ~ conc %col=% donor)) +
  labs(x   = "Ethanol [%]",
       y   = "Mobilité des spermatozoïdes [%]",
       col = "Donneur")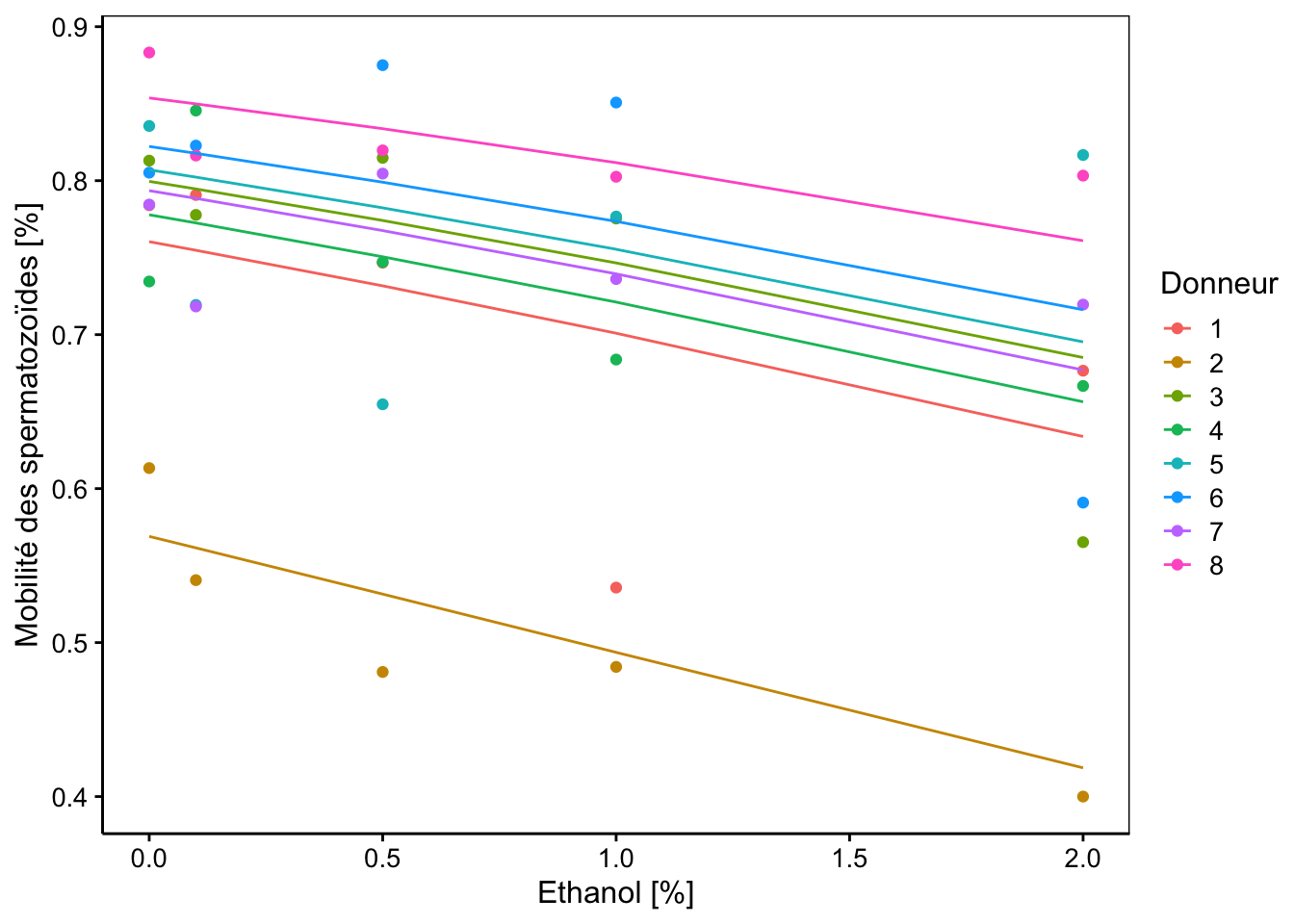

Les pentes sont donc bien ici toutes identiques cette fois, et nous avons montré que ce dernier modèle explique tout aussi bien les données obtenues que le précédent. Les tests z pour les paramètres fixes (ordonnée à l’origine et effet conc) indiquent que les deux paramètres sont significativement différents de zéro. Cependant, nous avons vu que ces tests étant approximatifs, nous devons plutôt recourir à d’autres mesures pour en estimer la significativité.

4.2.3 Intervalles de confiance des paramètres

Nous pouvons aussi calculer l’intervalle de confiance sur ces paramètres avec la fonction confint().

confint(spe_m2)

# Computing profile confidence intervals ...

#                  2.5 %     97.5 %
# .sig01       0.2695168  0.7719890
# (Intercept)  0.9261419  1.6176274
# conc        -0.3865530 -0.2192498

L’intervalle de confiance (à 95% par défaut, aussi noté IC ici) nous donne une information complémentaire sur l’estimation des paramètres. Ainsi la pente conc qui caractérise la diminution de mobilité spermatique en fonction de la concentration en éthanol a été estimée dans spe_m2 (voir le résumé plus haut) à -0.30. Son intervalle de confiance à 95% indique que la vraie valeur se trouve en réalité entre - 0.39 et -0.22 avec un degré de significativité \(\alpha\) de 5%. Nous pouvons aussi utiliser cette information pour déterminer si le paramètre est significativement différent de zéro. Il le sera, en effet, lorsque l’IC ne contiendra pas zéro, ce qui est le cas ici. Nous pouvons donc en conclure que l’éthanol a un effet négatif sur la mobilité spermatique chez l’homme.

Dans le tableau des intervalles de confiance, .sig01 correspond à la première variance (et seule ici) estimée pour le facteur aléatoire donor dont la valeur était estimée à 0,18 et donc, l’écart type est de 0,42 (racine carrée de la variance). L’IC 95% sur cet écart type est calculé comme compris entre 0.27 et 0.77. Il est donc lui-même également significatif puisqu’il ne comprend pas zéro.

Deux pièges ici :

1. Si le terme relatif à donor n’était pas significatif, nous pourrions être tentés de simplifier le modèle en l’éliminant et en effectuant alors une modèle linéaire généralisé classique entre cbind(mobile; total - mobile) et conc. Mais nous ne pouvons pas faire une telle simplification car le facteur fixe permet aussi de prendre en compte la répétition des mesures dans les mêmes échantillons. Si nous simplifions le modèle, nous considérerions alors que chaque mesure est indépendante des autres, sans prendre en compte que nous n’avons que huit donneurs en réalité. Ce serait faire de la pseudo-réplication !

2. D’un autre côté, les modèles mixtes n’aiment pas les paramètres (en particulier ceux des effets aléatoires) qui sont proches de la marge, c’est-à-dire, proches des valeurs limites. Ainsi, si une variance tend vers zéro, l’ajustement du modèle pourra produire des messages d’avis indiquant la présence de singularités, il ne pourra pas converger, ou il tombera sur d’autres erreurs encore. Les modèles mixtes sont effectivement plus difficiles à ajustés que leur homologues classiques. Dans ce cas, tentez un modèle plus simple, si vous le pouvez, ou jonglez avec les paramètres d’ajustement expliqués dans la page d’aide de ?lme4::glmer.

4.2.4 Difficultés d’ajustement

En cas de problème d’ajustement, nous pouvons vérifier si le modèle est singulier avec lme4::isSingular() et tester d’autres algorithmes d’optimisation avec lme4::allFit(). Ici, il n’y a pas de problèmes, mais nous pouvons quand même voir ce que cela donne :

lme4::isSingular(spe_m2)

# [1] FALSE

lme4::allFit(spe_m2)

# bobyqa : [OK]
# Nelder_Mead : [OK]
# nlminbwrap : [OK]
# optimx.L-BFGS-B : [OK]
# nloptwrap.NLOPT_LN_NELDERMEAD : [OK]
# nloptwrap.NLOPT_LN_BOBYQA : [OK]

# original model:
# cbind(mobile, total - mobile) ~ conc + (1 | donor) 
# data:  spe 
# optimizers (6): bobyqa, Nelder_Mead, nlminbwrap, optimx.L-BFGS-B,nloptwrap.NLOPT_LN_NELDERME...
# differences in negative log-likelihoods:
# max= 1.36e-07 ; std dev= 5.5e-08

La fonction lme4::allFit() utilise tous les optimiseurs qu’elle connait pour ajuster le modèle et en indique le résultat. Ici, tous ont pu ajuster correctement notre modèle.

L’équation du modèle qui est ajusté ici est assez complexe. Le package {equatiomatic} offre une fonction extract_eq qui génère l’équation LaTeX relative au modèle. Voici ce que cela donne dans le cas de spe_m2 :

\[ \begin{aligned} \operatorname{mobile}_{i} &\sim \operatorname{Binomial}(n = 1, \operatorname{prob}_{\operatorname{mobile} = 1} = \widehat{P}) \\ \log\left[\frac{\hat{P}}{1 - \hat{P}} \right] &=\alpha_{j[i]} + \beta_{1}(\operatorname{conc}) \\ \alpha_{j} &\sim N \left(\mu_{\alpha_{j}}, \sigma^2_{\alpha_{j}} \right) \text{, for donor j = 1,} \dots \text{,J} \end{aligned} \]

Le modèle est décrit en trois lignes. La première indique que la variable réponse mobile suit une distribution binomiale avec un nombre d’essais n = 1 et une probabilité de succès (spermatozoïde mobile) estimée à \(\hat P\). Dans la seconde ligne, nous avons la transformation logit de notre variable réponse (\(log[\hat P / (1 - \hat P)]\), notre fameuse fonction de lien) qui est modélisée comme une droite \(\alpha + \beta (conc)\). La troisième ligne indique enfin que \(\alpha\) suit une distribution normale de moyenne \(\mu_\alpha\) qui est notre ordonnée à l’origine moyenne, et d’écart type \(\sigma^2_\alpha\) qui est l’écart type calculé pour notre facteur aléatoire avec un indice j qui varie d’un donneur à l’autre.

4.2.5 Analyse des résidus

Pour les modèles linéaires généralisés, l’analyse des résidus ne se fait pas comme pour les modèles linéaires classiques, ou en tous cas pas pour tous les modèles. C’est pour cette raison que nous ne l’avions pas faite avec nos exemples de GLM. D’ailleurs, il y a plusieurs types de résidus. En plus des résidus classiques \(y_i - \hat y_i\) que vous connaissez bien, il y a aussi les résidus de Pearson qui vont divisés les résidus classiques par la variance du modèle en ce point (selon la distribution de la variable réponse, cette variance peut, en effet changer). Nous obtenons ces résidus en indiquant resid(mod, type = "pearson"). Nous pouvons tracer les graphiques des résidus en fonction des valeurs ajustées comme ceci :

chart(data = spe,
  resid(spe_m2, type = "pearson") ~ fitted(spe_m2) %col=% donor) +
  geom_point() +
  geom_hline(yintercept = 0) +
  labs(x = "Valeurs ajustées", y = "Résidus de Pearson")

Nous observons ici une distribution relativement correcte de ces résidus, à part un point extrême peut-être dans le bas du graphique. Attention ici que les valeurs ajustées dépendent du facteur aléatoire donor, et notamment, les points pour le donneur 2 en jaune sont toutes très faibles puisque cela correspond à la droite la plus basse sur le graphique du modèle. Ceci fait partie du modèle lui-même et ne doit donc pas être interprété comme une anomalie ici.

Nous pouvons réaliser un autre graphique de la racine carrée de la valeur absolue de ces résidus pour vérifier l’homoscédasticité (sachant qu’elle n’est pas rencontrée dans les résidus classiques, mais que les résidus de Pearson devraient, eux, voire leur variance stabilisée) :

chart(data = spe, sqrt(abs(resid(spe_m2, type = "pearson"))) ~ fitted(spe_m2) %col=% donor) +
  geom_point() +
  geom_hline(yintercept = 0) +
  labs(x = "Valeurs ajustées", y = "|Résidus de Pearson|^.5")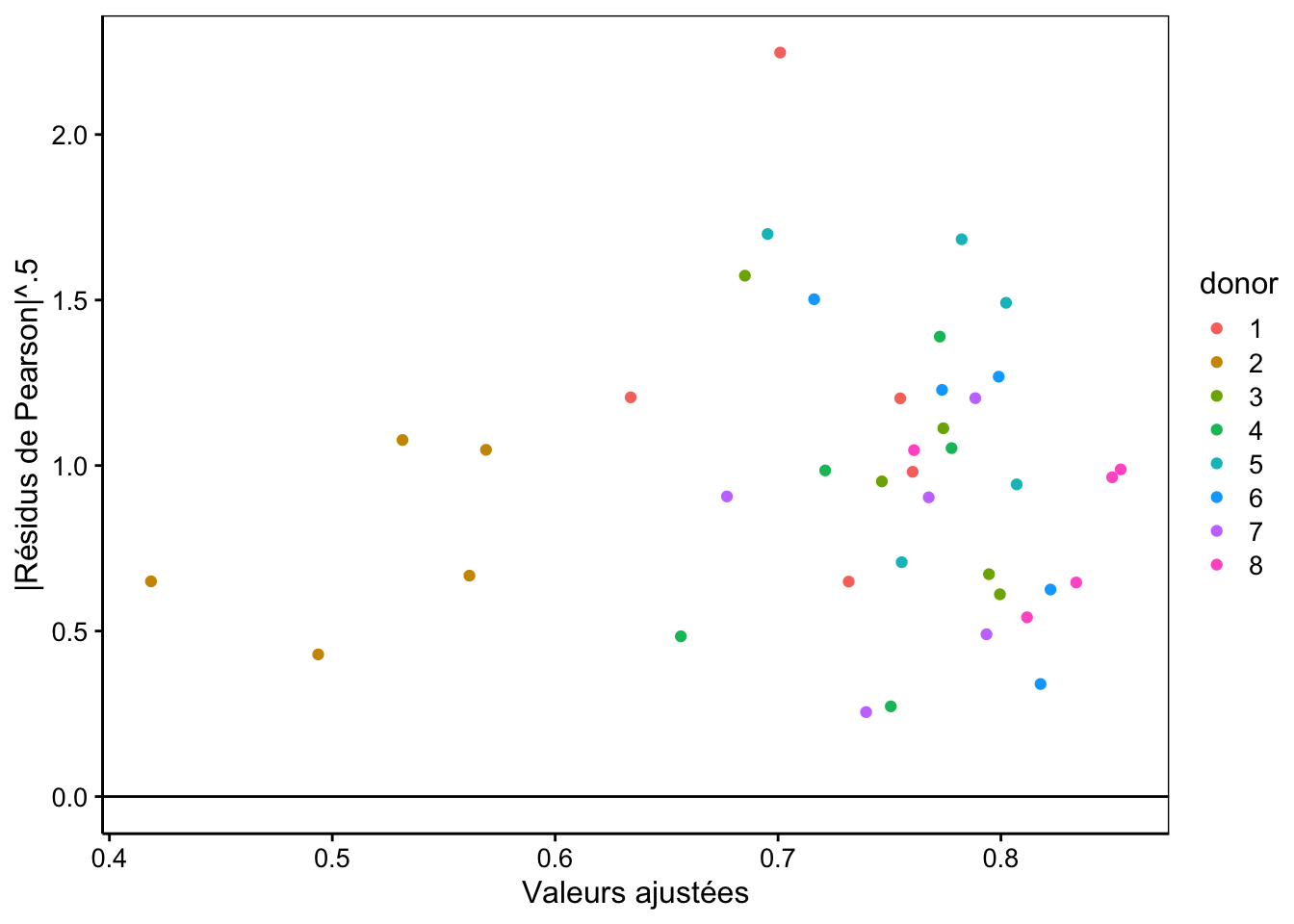

Nous ne voyons pas non plus d’anomalie particulière ici, à part toujours cette valeur extrême. Il est aussi possible d’étudier les résidus en fonction des variables explicatives à effet fixe, ici, conc :

chart(data = spe, resid(spe_m2, type = "pearson") ~ conc %col=% donor) +
  geom_point() +
  geom_hline(yintercept = 0) +
  labs(x = " Ethanol [%]", y = "Résidus de Pearson")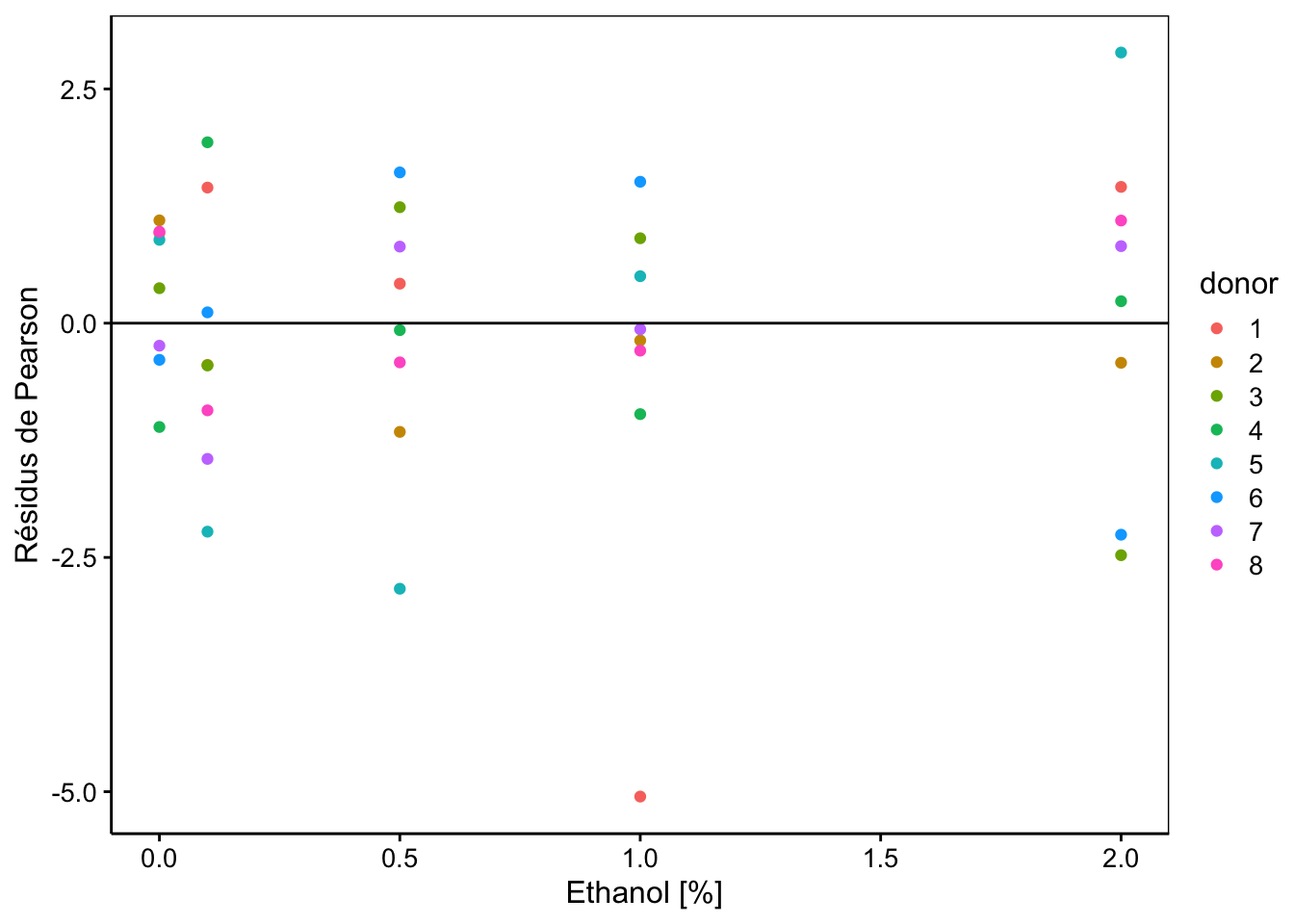

Même conclusion que pour les autres graphiques : pas de difficultés particulières à part une valeur extrême. Nous pourrions être tentés de vérifier la normalité des résidus. C’est facile à faire :

chart(data = spe, aes(sample = resid(spe_m2, type = "pearson"))) +
  geom_qq() +
  geom_qq_line()

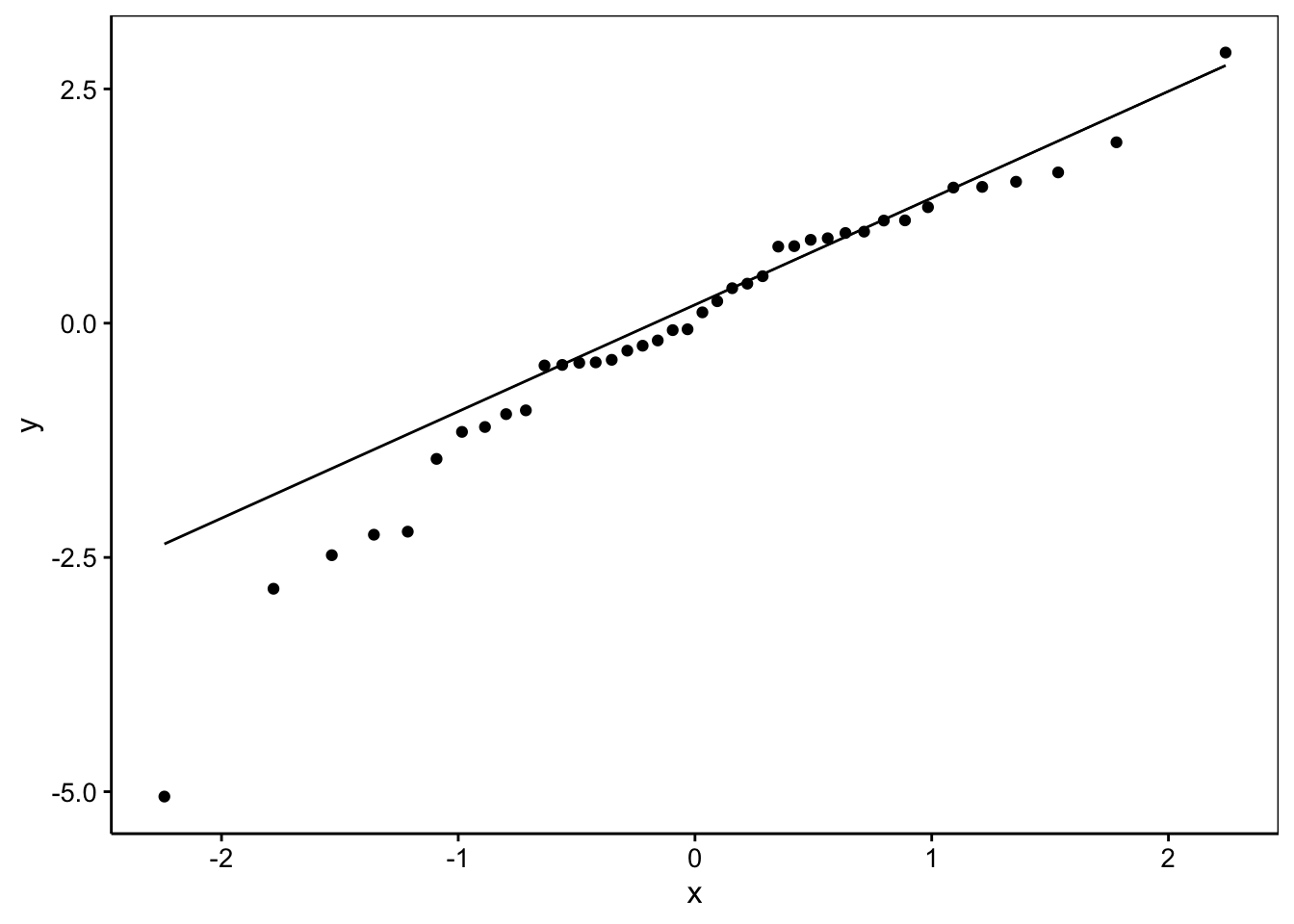
La normalité apparaît ici douteuse… et ce n’est pas grave, car pour les modèles linéaires généralisés l’hypothèse de normalité des résidus n’est pas nécessaire ! Seule l’homoscédasticité joue un rôle dans une certaine mesure, mais cela dépend des tests que vous utilisez. Si vous ne vous fiez pas aux tests z mais travaillez avec les intervalles de confiance, il existe une version bootstrappée qui calcule les intervalles de confiance de manière fiable même dans les cas limites. On utilisera confint(mod, level = 0.95, method = "boot", nsim = 500) où nsim = indique le nombre de fois que l’on va bootstrapper les données. Attention que ce calcul peut être très long !

À vous de jouer !

4.2.6 Prédictions à l’aide d’un GLMM

Les prédictions sont rendues difficiles à cause de deux modifications que nous avons introduites par rapport au modèle linéaire classique :

1. La fonction de lien qui transforme la variable réponse. Nous devons penser à appliquer la fonction inverse pour obtenir les estimations dans l’échelle d’origine de cette variable.

2. Les facteurs aléatoires ne permettent pas d’estimer précisément la variable réponse car, par définition, il y a une part de hasard introduite dans le modèle à travers la ou les distributions normales liées à ces facteurs aléatoires.

Il en résulte que les modèles (G)LMM sont beaucoup moins faciles à manipuler de ce point de vue. Voici quelques outils pour vous y aider. La fonction de lien et son inverse sont disponibles via make.link() qui renvoie une liste qui contient entre autre $linkfun et $linkinv. Ces dernières fonctions sont utilisables pour transformer dans un sens ou dans un autre les calculs. Pour notre fonction de lien logit, cela donne :

logit <- make.link("logit")
# Transforme quelques valeurs de Y (comprises entre 0 et 1, proportions)
y <- c(0.8, 0.85, 0.9, 0.95)
(y_logit <- logit$linkfun(y))

# [1] 1.386294 1.734601 2.197225 2.944439

# Retransforme en y à l'aide de la fonction inverse
(y2 <- logit$linkinv(y_logit))

# [1] 0.80 0.85 0.90 0.95

all.equal(y, y2)

# [1] TRUE

Nous pouvons maintenant tracer les graphiques qui montrent comment logit transforme nos valeurs Y :

dtbl(y = seq(0, 1, by = 0.001)) %>.%
  smutate(., y_logit = logit$linkfun(y)) %>.%
  chart(., y_logit ~ y) +
    geom_line()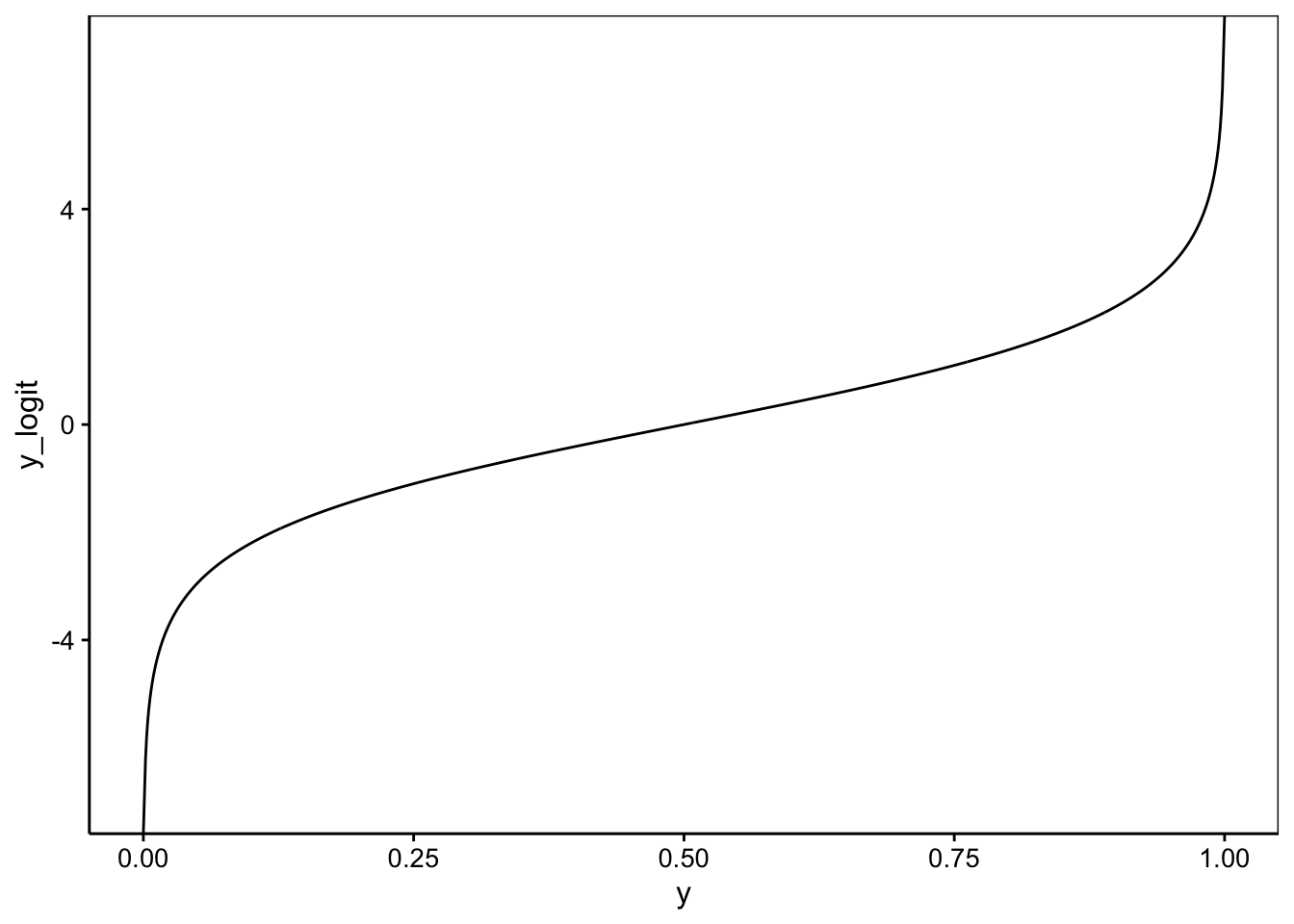

La transformation est d’autant plus forte que nous nous rapprochons des extrêmes, 0 ou 1. Effectuons un calcul à la main sur base de notre modèle spe_m2 dont les coefficients sont :

coef(spe_m2)

# $donor
#   (Intercept)       conc
# 1   1.1559378 -0.3029708
# 2   0.2880608 -0.3029708
# 3   1.3821835 -0.3029708
# 4   1.2533090 -0.3029708
# 5   1.4292835 -0.3029708
# 6   1.5288128 -0.3029708
# 7   1.3454443 -0.3029708
# 8   1.7588595 -0.3029708
# 
# attr(,"class")
# [1] "coef.mer"

Nous pourrions recalculer pour un donneur en particulier, mais si nous voulons un effet moyen, en faisant abstraction du donneur, nous devons nous concentrer sur les effets fixes uniquement, la fonction lme4::fixef() nous donne cette information (par opposition à lme4::ranef() qui nous renvoie uniquement les effets aléatoires) :

(spe_m2_fixef <- lme4::fixef(spe_m2))

# (Intercept)        conc 
#   1.2698292  -0.3029708

Comme nous avons une droite, calculer une prédiction manuellement semble simple. Il suffit de multiplier les concentrations en éthanol par la pente (-0.30) et lui ajouter l’ordonnée à l’origine (1.27).

intercept <- spe_m2_fixef[1]
slope <- spe_m2_fixef[2]
conc <- c(0, 0.25, 0.5, 1, 2)
slope * conc + intercept

# [1] 1.2698292 1.1940865 1.1183438 0.9668584 0.6638876

Nous obtenons des estimations de probabilité de mobilité de spermatozoïdes, mais dans l’échelle transformée logit. Nous ne devons donc pas oublier d’appliquer la transformée inverse pour obtenir ces probabilités, soit :

(mobi <- logit$linkinv(slope * conc + intercept))

# [1] 0.7807135 0.7674711 0.7536814 0.7244929 0.6601331

Donc, si nous voulons déterminer de combien la mobilité des spermatozoïdes diminue avec, disons une concentration en éthanol de 1% selon notre modèle, nous pouvons soustraire de la première valeur de mobi (pour une concentration de 0, la valeur prédite pour 1%, soit la 4^e valeur de mobi).

mobi[1] - mobi[4]

# [1] 0.05622064

La diminution estimée est de 6,5%.

Pour en savoir plus…

De manière générale, les modèles linéaires, GLM, GLMM sont compliqués et il y a beaucoup de pièges. Plus tard, nous vous conseillons de toujours faire vérifier vos modèles par un statisticien chevronné. Les documents ci-dessous peuvent vous aider toutefois si vous travaillez seul.

• Un document ultra complet en français sur les GLM.

• Un autre, toujours en français et qui cible leur utilisation en écologie.

• Les modèles linéaires mixtes (LMM) se traitent de la même façon, mais avec la fonction lme4::lmer(). Voyez par exemple ici en français.

• Une FAQ sur les GLMM en anglais. Ce document est une mine d’or avec énormément de bons conseils !

• Résidus d’une GLM en anglais. Explique les différents types de résidus d’un modèle GLM.

• GLM in R for Ecology en anglais. Un document très complet sur les GLM en écologie.

À vous de jouer !

Réalisez le travail B04Ia_lungcap.

Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques II à l’UMONS (Q1 : modélisation) à terminer avant le 2024-11-25 23:59:59.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md.

Réalisez en groupe le travail B02Ga_models, partie III.

Travail en groupe de 4 pour les étudiants inscrits au cours de Science des Données Biologiques II à l’UMONS (Q1 : modélisation) à terminer avant le 2024-12-17 23:59:59.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md, partie III.