6.4 K-moyennes

Les k-moyennes (ou k-means en anglais) représentent une autre façon de regrouper les individus d’un tableau multivarié. Par rapport à la CAH, cette technique est généralement moins efficace, mais elle a l’avantage de permettre le regroupement d’un très grand nombre d’individus (gros jeu de données), là où la CAH nécessiterait trop de temps de calcul et de mémoire vive. Il est donc utile de connaître cette seconde technique à utiliser comme solution de secours lorsque le dendrogramme de la CAH devient illisible sur de très gros jeux de données.

À vous de jouer !

Le principe des k-moyennes est assez simple¹⁶ :

L’utilisateur choisit à l’avance le nombre de groupes k qu’il veut obtenir.
La position des k centres est placée au hasard au début.
Les individus sont attribués aux k groupes en fonction de leurs distances aux centres (attribution au groupe de centre le plus proche).
Les k centres sont relocalisés au centre de gravité des groupes ainsi obtenus.
Les individus sont réaffectés en fonction de leurs distances à ces nouveaux centres.
Si au moins un individu a changé de groupe, le calcul est réitéré. Sinon, nous considérons avoir atteint la configuration finale.

La technique est illustrée dans la vidéo suivante :

Essayez par vous-même via l’application ci-dessous qui utilise le célèbre jeu de données iris. Notez que vous devez utiliser des variables numériques. Par exemple, Species étant une variable qualitative, vous verrez que cela ne fonctionne pas dans ce cas.

6.4.1 Exemple simple

R propose la fonction kmeans() et différents packages la supplémentent pour enrichir votre boite à outils. Nous rassemblons tout cela sous une interface cohérente dans SciViews autour d’une fonction légèrement différente : k_means(). Vous rendez cette fonction disponible grâce à l’instruction SciViews::R("explore").

SciViews::R("explore")

Vous avez les méthodes print(), plot(), autoplot(), chart(), augment(), tidy(), glance(), predict() et fitted(). Nous verrons leur utilisation au fur et à mesure des explications dans cette partie. Enfin, la fonction profile_k() permet de rechercher k, le nombre optimal de clusters à réaliser.

Afin de comparer la classification par k-moyennes à celle par CAH, nous reprendrons ici le même jeu de données zooplankton.

zoo <- read("zooplankton", package = "data.io")
zoo

#             ecd   area perimeter  feret  major  minor   mean  mode   min   max
#           <num>  <num>     <num>  <num>  <num>  <num>  <num> <num> <num> <num>
#    1: 0.7697829 0.4654    4.4469 1.3168 1.1640 0.5091 0.3631 0.036 0.004 0.908
#    2: 0.7004136 0.3853    2.3247 0.7281 0.7128 0.6882 0.3609 0.492 0.024 0.676
#    3: 0.8147804 0.5214    4.1509 1.3267 1.1106 0.5978 0.3082 0.032 0.008 0.696
#    4: 0.7850146 0.4840    4.4422 1.7845 1.5641 0.3940 0.3317 0.036 0.004 0.728
#    5: 0.3614338 0.1026    1.7065 0.7391 0.6940 0.1883 0.1526 0.016 0.008 0.452
#   ---                                                                         
# 1258: 0.5579490 0.2445    4.6214 0.9864 0.7318 0.4254 0.0329 0.012 0.004 0.300
# 1259: 0.4763311 0.1782    4.2148 0.9864 0.5593 0.4057 0.1474 0.016 0.004 0.508
# 1260: 0.5744769 0.2592    5.4060 0.9302 0.7010 0.4709 0.0374 0.012 0.004 0.304
# 1261: 0.6375093 0.3192    6.9642 1.6955 0.7468 0.5443 0.1576 0.008 0.004 0.600
# 1262: 0.5817449 0.2658    5.1730 1.0174 0.6401 0.5288 0.1292 0.008 0.004 0.536
#       std_dev range    size    aspect elongation compactness transparency
#         <num> <num>   <num>     <num>      <num>       <num>        <num>
#    1:  0.2313 0.904 0.83655 0.4373711   8.504961    3.381259 0.0798124665
#    2:  0.1831 0.652 0.70050 0.9654882   1.000000    1.116156 0.0001233552
#    3:  0.2039 0.688 0.85420 0.5382676   6.097393    2.629685 0.0461479759
#    4:  0.2178 0.724 0.97905 0.2519021   8.068804    3.244449 0.1981874152
#    5:  0.1099 0.444 0.44115 0.2713256   4.891424    2.258683 0.1807009408
#   ---                                                                    
# 1258:  0.0415 0.296 0.57860 0.5813064  19.787231    6.951178 0.0356913516
# 1259:  0.1477 0.504 0.48250 0.7253710  22.878484    7.932980 0.0127853501
# 1260:  0.0456 0.300 0.58595 0.6717546  26.149293    8.972371 0.0195803673
# 1261:  0.1903 0.596 0.64555 0.7288431  35.957843   12.091209 0.0124556351
# 1262:  0.1273 0.532 0.58445 0.8261209  23.125992    8.011616 0.0046285389
#       circularity density            class
#             <num>   <num>           <fctr>
#    1:      0.2958  0.1690 Poecilostomatoid
#    2:      0.8959  0.1390        Egg_round
#    3:      0.3803  0.1607         Calanoid
#    4:      0.3082  0.1606 Poecilostomatoid
#    5:      0.4429  0.0157     Harpacticoid
#   ---                                     
# 1258:      0.1438  0.0080 Poecilostomatoid
# 1259:      0.1261  0.0263         Calanoid
# 1260:      0.1115  0.0097 Poecilostomatoid
# 1261:      0.0827  0.0503         Calanoid
# 1262:      0.1248  0.0344         Calanoid

Commençons par l’exemple simplissime de la réalisation de deux groupes à partir de six individus issus de ce jeu de données, comme nous l’avons fait avec la CAH :

zoo %>.%
  select(., -class) %>.% # Élimination de la colonne class
  slice(., 13:18) ->   # Récupération des lignes 13 à 18
  zoo6

# Ne pas oublier de standardiser avec scale()
zoo6_kmn <- k_means(scale(zoo6), k = 2)
zoo6_kmn

# K-means clustering with 2 clusters of sizes 3, 3
# 
# Cluster means:
#          ecd       area  perimeter      feret      major      minor       mean
# 1  0.8513216  0.8392524  0.8799568  0.7696708  0.6691858  0.7425983  0.5437486
# 2 -0.8513216 -0.8392524 -0.8799568 -0.7696708 -0.6691858 -0.7425983 -0.5437486
#         mode        min        max    std_dev      range       size      aspect
# 1  0.3144358 -0.5201565  0.6542561  0.7043179  0.6597191  0.8271838  0.06931258
# 2 -0.3144358  0.5201565 -0.6542561 -0.7043179 -0.6597191 -0.8271838 -0.06931258
#   elongation compactness transparency circularity    density
# 1  0.7375994   0.7373144   -0.4355018  -0.5926864  0.7253086
# 2 -0.7375994  -0.7373144    0.4355018   0.5926864 -0.7253086
# 
# Clustering vector:
# [1] 2 1 2 1 1 2
# 
# Within cluster sum of squares by cluster:
# [1] 14.32167 28.69886
#  (between_SS / total_SS =  54.7 %)
# 
# Available components:
# 
#  [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
#  [6] "betweenss"    "size"         "iter"         "ifault"       "data"

Nous voyons que la fonction k_means() effectue notre classification¹⁷. Nous lui fournissons le tableau de départ et spécifions le nombre k de groupes souhaités via l’argument k =. Ne pas oublier de standardiser les données si les variables sont dans des unités différentes et/ou si leurs valeurs diffèrent de manière importante entre les colonnes. N’oubliez pas non plus d’assigner le résultat du calcul à une nouvelle variable, ici zoo6_kmn, pour pouvoir l’inspecter et l’utiliser par la suite. L’impression du contenu de l’objet nous donne plein d’information dont :

le nombre d’individus dans chaque groupe (ici 3 et 3),
la position des centres pour les k groupes dans Cluster means,
l’appartenance aux groupes dans Clustering vector (dans le même ordre que les lignes du tableau de départ),
la somme des carrés des distances entre les individus et la moyenne au sein de chaque groupe dans Within cluster sum of squares ; le calcul between_SS / total_SS est à mettre en parallèle avec le R² de la régression linéaire : c’est une mesure de la qualité de regroupement des données (plus la valeur est proche de 100% mieux c’est, mais attention que cette valeur augmente d’office en même temps que k),
et enfin, la liste des composants accessibles avec l’opérateur $ ; par exemple, pour obtenir la taille de chaque groupe (en nombre d’individus), nous ferons :

zoo6_kmn$size

# [1] 3 3

Le package {broom} contient trois fonctions complémentaires qui nous seront utiles : tidy(), augment() et glance(). broom::glance() retourne un data.frame avec les statistiques permettant d’évaluer la qualité de la classification obtenue :

glance(zoo6_kmn)

# # A tibble: 1 × 4
#   totss tot.withinss betweenss  iter
#   <dbl>        <dbl>     <dbl> <int>
# 1    95         43.0      52.0     1

Si nous voulons déterminer la valeur optimale de k, nous pouvons utiliser profile_k() appliqué au jeu de données initial, ou à la composante data de notre objet k_means (spécifier éventuellement une valeur différente de celle par défaut pour l’argument k.max = de la fonction, voir l’aide en ligne de ?factoextra::fviz_nbclust) dont profile_k() dérive :

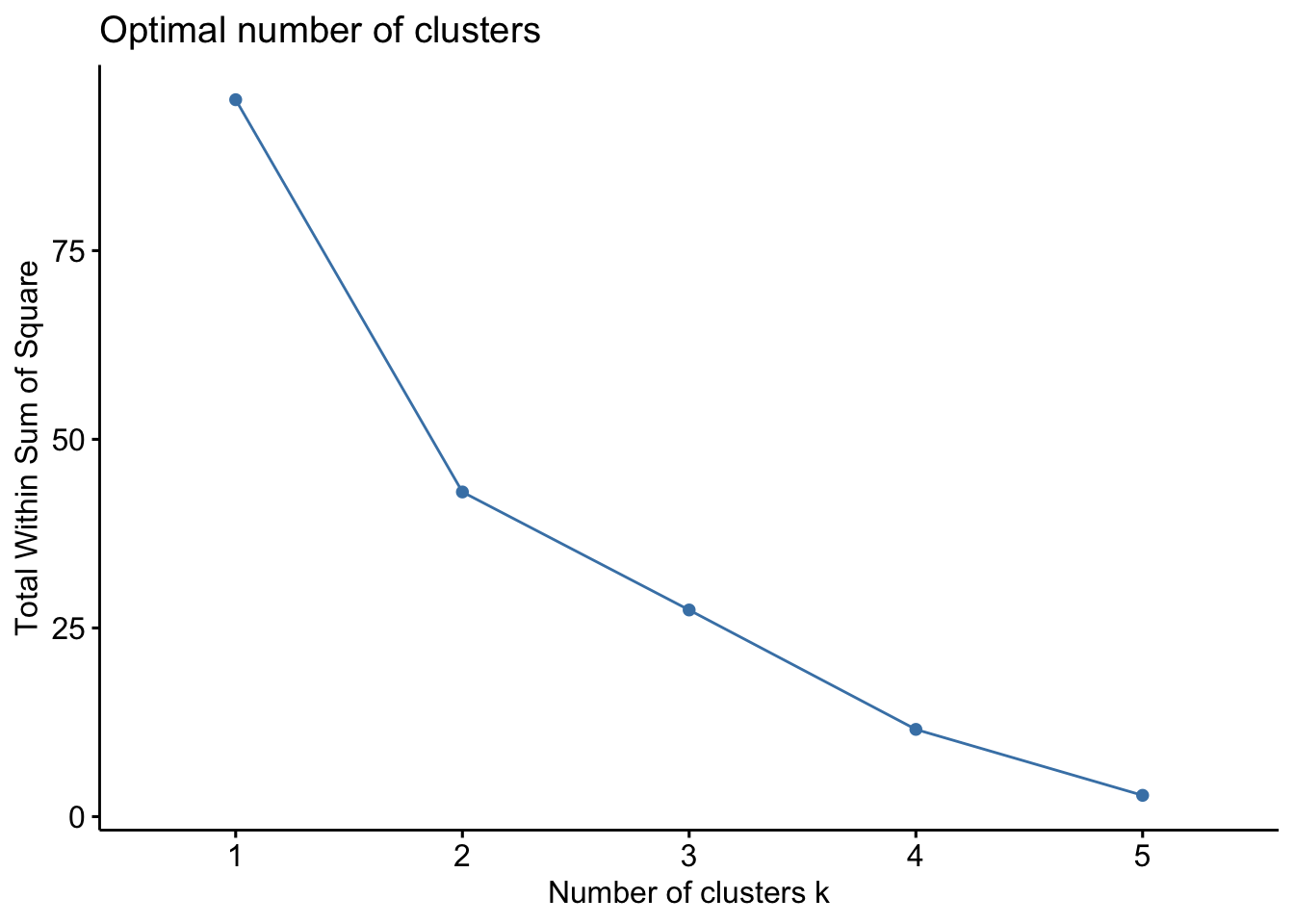
profile_k(scale(zoo6)) # ou zoo6_kmn$data

Le graphique obtenu montre la décroissance de la somme des carrés des distances intragroupes en fonction de k. Avec k = 1, nous considérons toutes les données dans leur ensemble et nous avons la somme des carrés des distances euclidiennes entre tous les individus et le centre de gravité du nuage de points dont les coordonnées sont les moyennes de chaque variable. C’est le point de départ qui nous indique de combien les données sont dispersées (la valeur absolue de ce nombre n’est pas importante).

Ensuite, avec k croissant, notre objectif est de faire des regroupements qui diminuent la variance intragroupe autant que possible, ce que nous notons par la diminution de la somme des carrés intragroupes (la variance du groupe est, en effet, la somme des carrés des distances euclidiennes entre les points et le centre du groupe, divisée par les degrés de liberté).

Nous recherchons ici des sauts importants dans la décroissance de la somme des carrés, tout comme dans le dendrogramme obtenu par la CAH nous recherchions des sauts importants dans les regroupements (hauteur des barres verticales du dendrogramme). Nous observons ici un saut important pour k = 2, puis une diminution un peu moins forte. Ceci suggère que nous pourrions considérer deux groupes, mais qu’un regroupement plus détaillé a quand même un sens ici.

Le nombre de groupes proposé par profile_k() n’est qu’indicatif ! Si vous avez par ailleurs d’autres informations qui vous suggèrent un regroupement différent, ou si vous voulez essayer un regroupement plus ou moins détaillé par rapport à ce qui est proposé, c’est tout aussi correct.

La fonction profile_k() propose d’ailleurs deux autres méthodes pour déterminer le nombre optimal de groupes k, avec method = "silhouette" ou method = "gap_stat". Voyez l’aide en ligne de la fonction ?factoextra::fviz_nbclust. Ces différentes méthodes peuvent d’ailleurs suggérer des regroupements différents pour les mêmes données… preuve qu’il n’y a pas une et une seule solution optimale !

A ce stade, nous pouvons collecter les groupes et les ajouter à notre tableau de données avec augment(). Notez que si vous voulez juste récupérer les groupes, vous pouvez utiliser alors predict(zoo6_kmn). augment() crée une nouvelle colonne nommée .cluster que nous renommons ici immédiatement en cluster, et ensuite, nous enregistrons le tout dans un nouveau jeu de données nommé zoo6b¹⁸.

augment(zoo6_kmn, zoo6) %>.%
  srename(., cluster = .cluster) ->
  zoo6b
names(zoo6b)

#  [1] "ecd"          "area"         "perimeter"    "feret"        "major"       
#  [6] "minor"        "mean"         "mode"         "min"          "max"         
# [11] "std_dev"      "range"        "size"         "aspect"       "elongation"  
# [16] "compactness"  "transparency" "circularity"  "density"      "cluster"

La nouvelle variable cluster contient ceci :

zoo6b$cluster

# [1] 2 1 2 1 1 2
# Levels: 1 2

C’est le contenu de zoo6_kmn$cluster, mais transformé en variable factor.

class(zoo6b$cluster)

# [1] "factor"

Nous pouvons enfin utiliser tidy() pour obtenir un tableau avec les coordonnées des k centres. Nous l’enregistrerons dans la variable zoo6_centers, en ayant bien pris soin de nommer les variables du même nom que dans le tableau original zoo6 (argument col.names = names(zoo6), afin de conserver le nom de nos variables initiales dans ce nouveau tableau :

zoo6_centers <- tidy(zoo6_kmn, col.names = names(zoo6))
zoo6_centers

# # A tibble: 2 × 21
#      ecd   area perimeter  feret  major  minor   mean   mode    min    max
#    <dbl>  <dbl>     <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>  <dbl>
# 1  0.851  0.839     0.880  0.770  0.669  0.743  0.544  0.314 -0.520  0.654
# 2 -0.851 -0.839    -0.880 -0.770 -0.669 -0.743 -0.544 -0.314  0.520 -0.654
# # ℹ 11 more variables: std_dev <dbl>, range <dbl>, size <int>, aspect <dbl>,
# #   elongation <dbl>, compactness <dbl>, transparency <dbl>, circularity <dbl>,
# #   density <dbl>, withinss <dbl>, cluster <fct>

La dernière colonne de ce tableau est également nommée cluster. C’est le lien entre le tableau zoo6b augmenté et zoo6_centers.

Un outre outil très utile est la représentation graphique du regroupement effectué par nos k-moyennes sur un graphique en nuage de points. Évidemment, on ne peut choisir que deux variables parmi l’ensemble de celles qui sont utilisées pour le calcul (argument choices =).

kmn_chart <- chart(zoo6_kmn, choices = c("circularity", "area"),
  alpha = 0.8, c.size = 5, c.shape = 17)
kmn_chart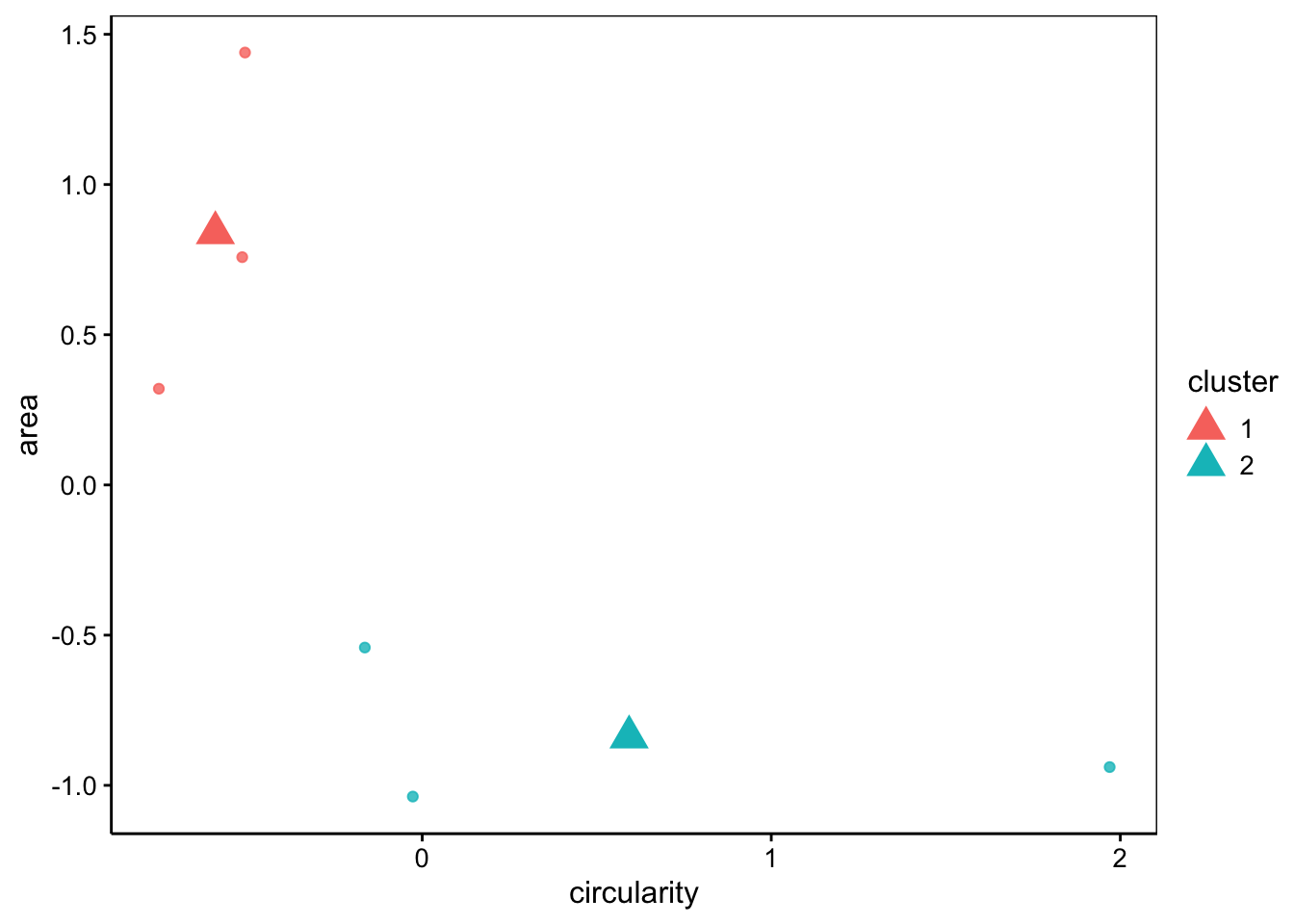

Les arguments optionnels c.size = et c.shape = contrôlent l’apparence des centres des groupes. L’argument optionnel alpha = gère la semi-transparence des points, utile si vous avez beaucoup de points à afficher sur le graphique. À noter que nos variables étant standardisées avec scale(), les échelles des axes X et Y ne correspondent plus aux valeurs, ni aux unités initiales. De plus, les labels ont été perdus. Donc, vous pourriez y rajouter des labels plus informatifs pour indiquer que les valeurs sont standardisées :

kmn_chart +
  labs(x = "Circularité standardisée", y = "Aire standardisée")

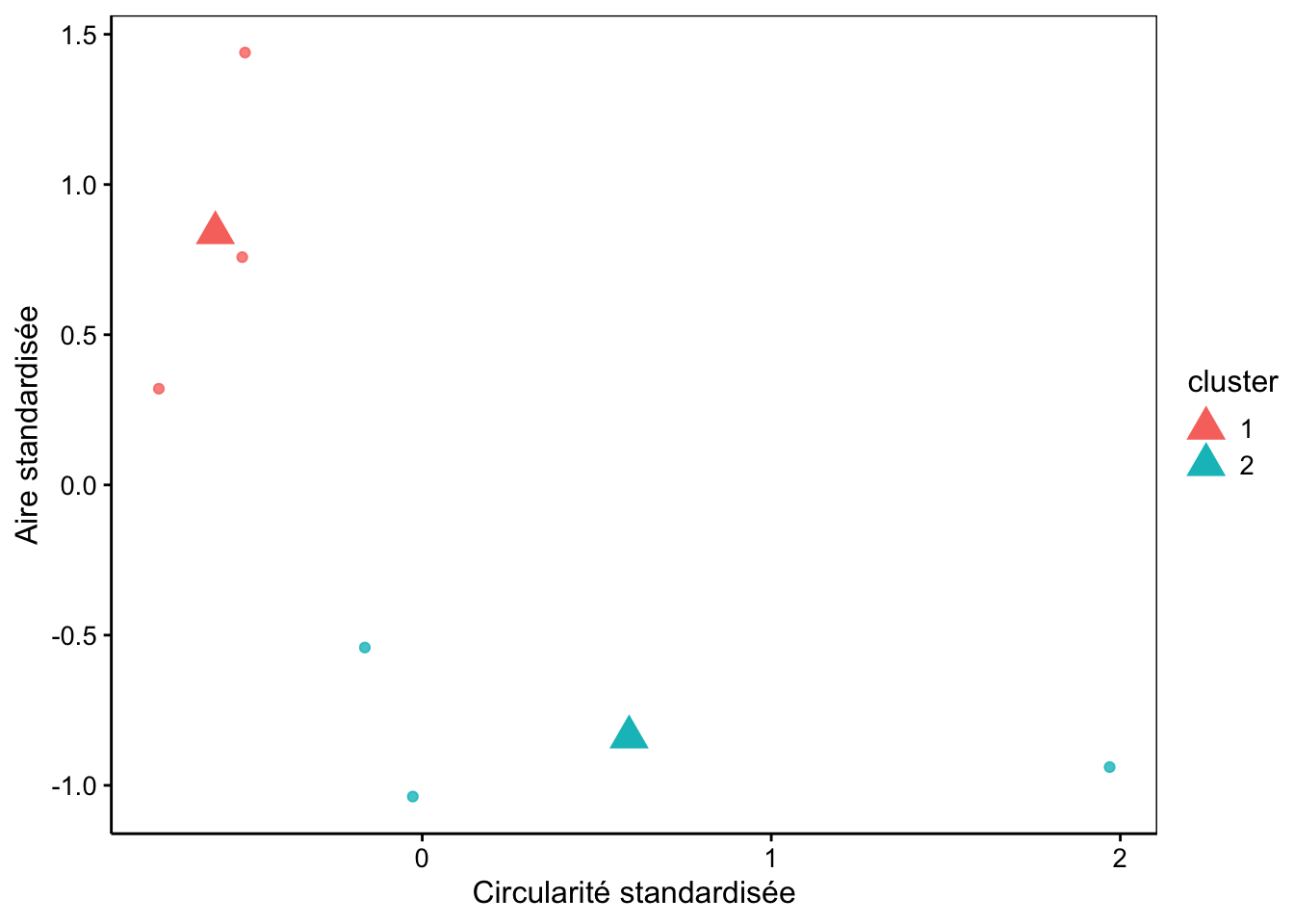
Comparez avec le graphique équivalent obtenu à l’aide de la CAH. Outre que l’ordre des groupes est inversé, et que les données sont standardisées dans le présent graphique, un point est classé dans un groupe différent par les deux méthodes. Il s’agit du point ayant environ -0.2 de circularité standardisée et -0.5 d’aire standardisée. Comme nous connaissons par ailleurs la classe à laquelle appartient chaque individu, nous pouvons la récupérer comme colonne supplémentaire du tableau et ajouter cette information sur notre graphique. Cela nécessite cependant un petit peu de travail pour créer un jeu de données ne contenant que les 6 items avec les mesures standardisées et leur classe.

# Données standardisées + classe pour les individus de 13 à 18 de zoo
zoo6std <- scale(zoo6)
zoo6std$class <- zoo$class[13:18] 
# Graphique annoté des classes
kmn_chart +
  labs(x = "Circularité standardisée", y = "Aire standardisée") +
  ggrepel::geom_text_repel(data = zoo6std, aes(label = class))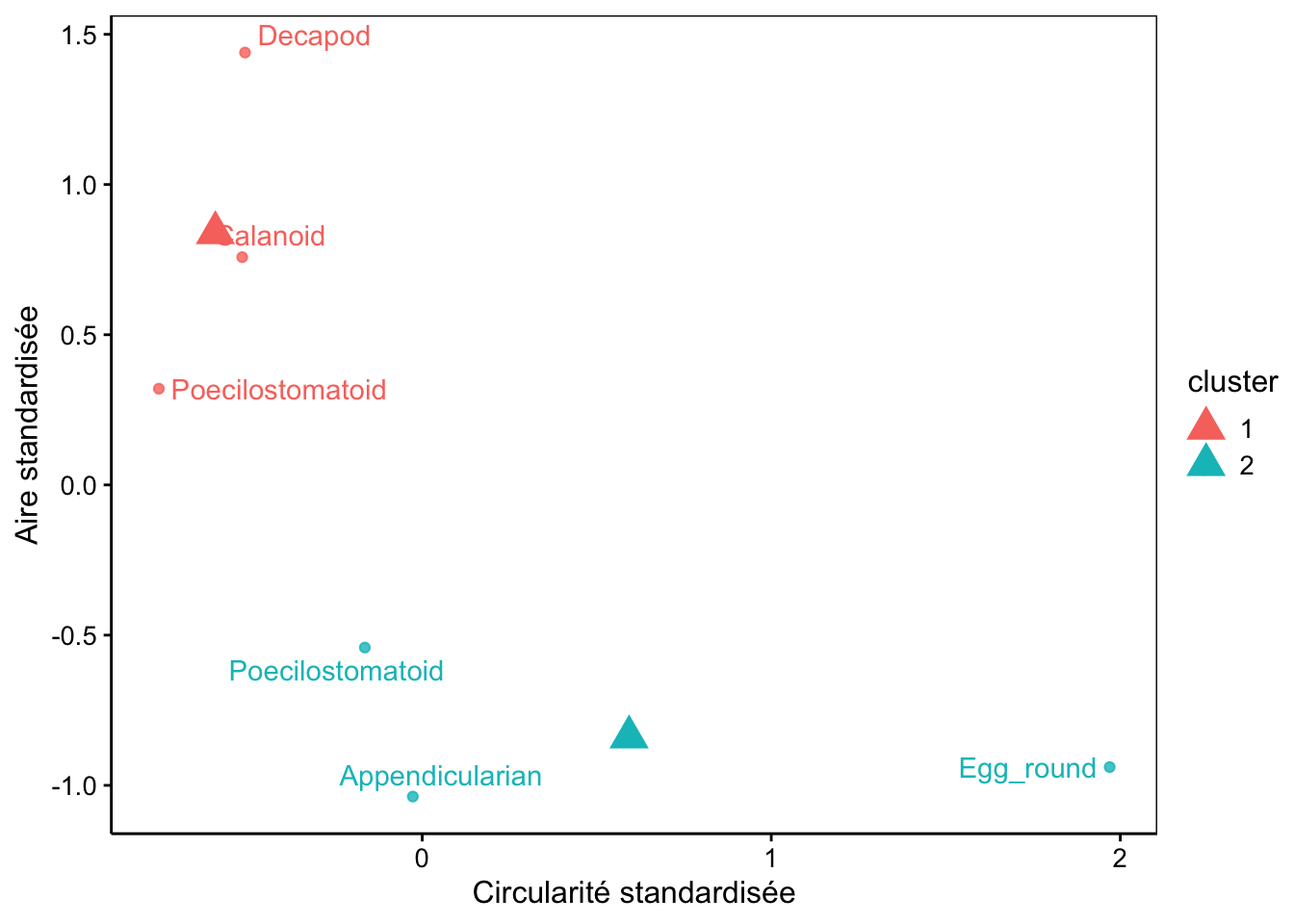

Nous constatons que le point classé différemment est un “Poecilostomatoïd”. Or, l’autre groupe des k-moyennes contient aussi un individu de la même classe. Donc, la CAH a mieux classé notre plancton que les k-moyennes dans le cas présent. Ce n’est pas forcément toujours le cas, mais souvent.

Comme les k-moyennes partent d’une position aléatoire des k centres, le résultat final peut varier et n’est pas forcément optimal. Pour éviter cela, nous pouvons indiquer à k_means() d’essayer différentes situations de départ via l’argument nstart =. Par défaut, nous prenons une seule situation aléatoire de départ nstart = 1, mais en indiquant une valeur plus élevée pour cet argument, il est possible d’essayer plusieurs situations de départ et ne garder que le meilleur résultat final. Cela donne une analyse plus robuste et plus reproductible… mais le calcul est naturellement plus long.

k_means(zoo6, k = 2, nstart = 50) # 50 positions de départ différentes

# K-means clustering with 2 clusters of sizes 3, 3
# 
# Cluster means:
#         ecd      area perimeter    feret    major     minor      mean      mode
# 1 0.6292647 0.3188667  3.224133 1.159200 1.096433 0.4023333 0.1871667 0.1026667
# 2 1.1926500 1.1279667 10.346667 2.201133 1.677067 0.8596333 0.3217333 0.3533333
#          min       max   std_dev     range      size    aspect elongation
# 1 0.01066667 0.5400000 0.1166667 0.5293333 0.7493833 0.4753843   6.333315
# 2 0.00400000 0.8986667 0.2620000 0.8946667 1.2683500 0.5149422  23.046713
#   compactness transparency circularity    density
# 1    2.727708   0.14732060   0.4900333 0.06943333
# 2    7.987806   0.06173831   0.1357000 0.37630000
# 
# Clustering vector:
# [1] 1 2 1 2 2 1
# 
# Within cluster sum of squares by cluster:
# [1]  54.18647 200.03837
#  (between_SS / total_SS =  68.1 %)
# 
# Available components:
# 
#  [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
#  [6] "betweenss"    "size"         "iter"         "ifault"       "data"

Dans ce cas simple, cela ne change pas grand-chose. Mais avec un plus gros jeu de données plus complexe, cela peut être important.

À vous de jouer !

6.4.2 Classification du zooplancton

Maintenant que nous savons utiliser k_means() et les fonctions annexes, nous pouvons classer le jeu de données zoo tout entier.

zoo %>.%
  sselect(., -class) %>.%
  scale(.) %>.%
  profile_k(., k.max = 15)

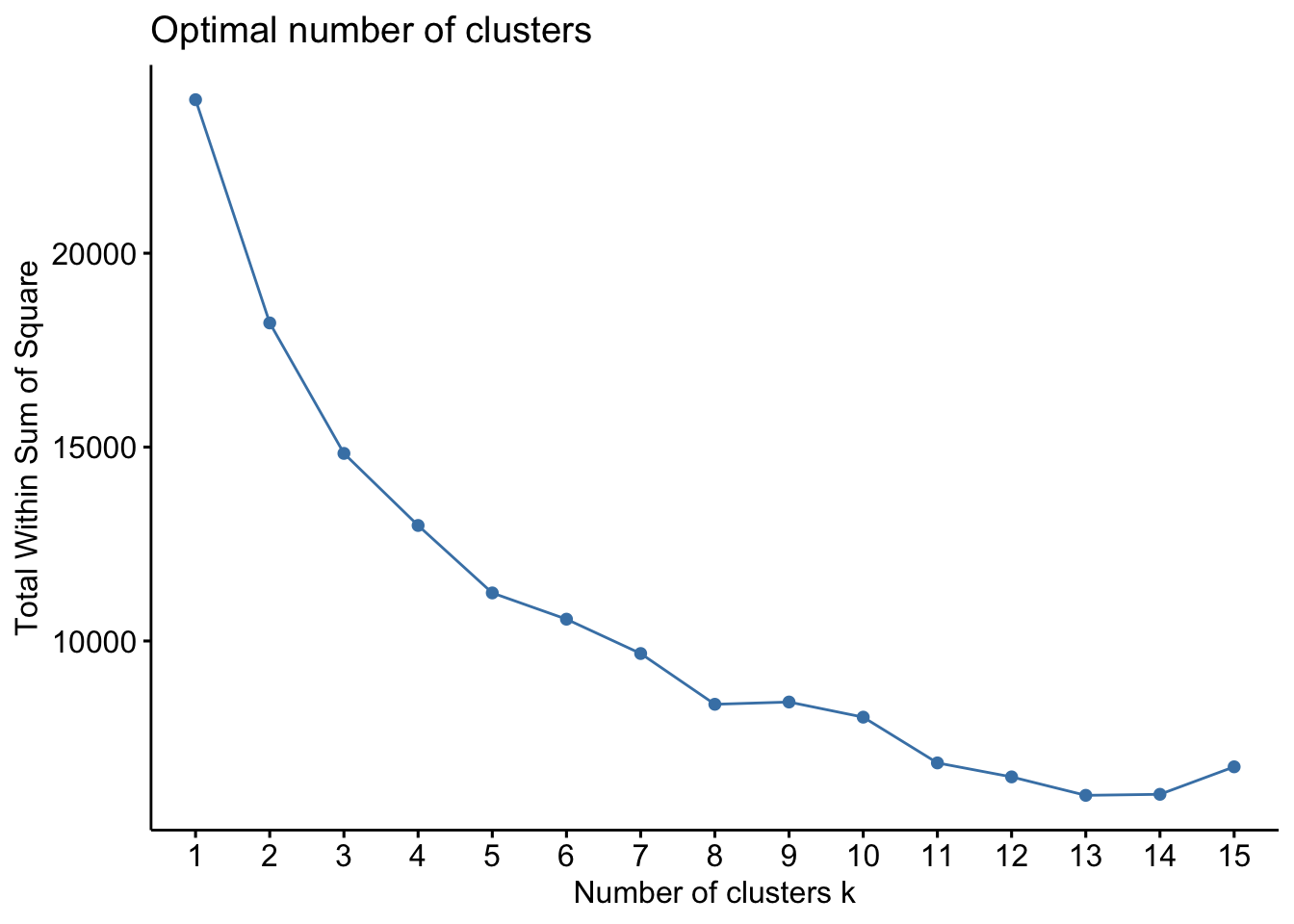
Nous observons un saut maximal pour k = 2, mais le saut pour k = 3 est encore conséquent. Afin de comparer avec ce que nous avons fait par CAH, nous utiliserons donc k = 3. Enfin, comme un facteur aléatoire intervient, qui définira au final le numéro des groupes, nous utilisons set.seed() pour rendre l’analyse reproductible. Pensez à donner une valeur différente à cette fonction pour chaque utilisation ! Pensez aussi à éliminer les colonnes non numériques à l’aide de sselect() et à standardiser avec scale() si c’est nécessaire.

set.seed(562)
sselect(zoo, -class) %>.%
  scale(.) %>.%
  k_means(., k = 3, nstart = 50) ->
  zoo_kmn
zoo_kmn

# K-means clustering with 3 clusters of sizes 511, 661, 90
# 
# Cluster means:
#          ecd       area   perimeter       feret      major       minor
# 1 -0.2517071 -0.1819975 -0.41913500 -0.42842705 -0.2767871 -0.15229969
# 2 -0.1702276 -0.1483124 -0.01053525 -0.05604782 -0.1944370 -0.08840095
# 3  2.6793643  2.1226136  2.45713094  2.84415368  2.9995675  1.51397969
#         mean       mode        min        max    std_dev      range       size
# 1  0.7646541  0.3099542  0.5011815  0.8338167  0.8004033  0.8284225 -0.2808581
# 2 -0.5364261 -0.2654678 -0.3404820 -0.6855013 -0.5263938 -0.6824966 -0.1926062
# 3 -0.4017846  0.1898626 -0.3449459  0.3004002 -0.6784421  0.3089594  3.0092357
#        aspect elongation compactness transparency circularity     density
# 1  0.10273406 -0.5798725  -0.5782663  -0.23720081   0.5630402 -0.03959989
# 2  0.07589772  0.2925602   0.2911364  -0.07155467  -0.3378906 -0.23950775
# 3 -1.14072772  1.1436952   1.1450326   1.87230280  -0.7151979  1.98389075
# 
# Clustering vector:
#    [1] 1 1 1 1 2 1 2 1 2 1 3 2 1 1 1 1 2 2 2 2 1 2 1 1 2 1 1 2 1 1 1 2 1 1 2 1 2
#   [38] 2 2 1 2 1 2 2 1 1 2 1 1 1 1 2 2 1 1 2 1 2 2 1 2 1 1 2 1 2 2 1 1 1 1 2 2 2
#   [75] 1 1 1 1 1 1 1 1 1 1 1 2 2 1 2 1 1 2 1 3 1 1 1 2 1 2 1 1 1 1 2 1 2 2 2 2 1
#  [112] 1 1 1 1 2 2 1 1 1 2 2 1 1 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 2 2 1 1 3 3 3 2
#  [149] 2 1 1 1 1 2 1 3 2 2 1 2 2 1 2 2 1 1 1 2 1 1 2 2 1 1 1 1 2 2 2 2 1 1 2 1 2
#  [186] 1 1 2 1 1 1 1 2 1 2 2 1 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 1 2 1 2 1 2 1 1
#  [223] 1 1 1 2 1 1 1 1 2 1 2 2 2 1 2 2 1 1 2 1 2 2 2 2 2 2 1 2 1 2 2 2 1 1 2 2 2
#  [260] 2 2 2 2 2 1 1 2 2 3 3 3 1 1 3 1 2 2 1 2 1 1 3 1 1 3 1 1 3 2 3 2 2 1 1 1 1
#  [297] 1 2 3 1 2 1 2 2 1 2 2 1 3 1 2 2 2 1 3 3 3 1 3 2 2 2 2 1 2 2 1 2 2 2 2 1 1
#  [334] 2 2 2 1 2 1 2 2 1 1 2 1 1 2 2 2 1 2 2 1 1 2 2 1 1 1 1 1 1 2 1 1 2 1 2 1 1
#  [371] 1 1 1 1 1 1 1 2 1 1 1 2 2 1 1 1 1 1 1 1 1 1 2 1 1 1 1 2 1 1 1 2 1 1 1 1 1
#  [408] 2 1 1 1 2 2 1 1 1 1 1 1 2 2 2 2 2 1 2 2 1 1 1 2 2 3 1 1 2 1 2 1 1 2 3 2 2
#  [445] 2 2 2 1 2 1 2 1 3 2 1 2 2 2 2 1 1 1 2 1 2 1 1 2 1 1 1 2 2 2 2 2 2 1 2 1 1
#  [482] 1 1 2 2 1 1 2 1 2 2 2 2 2 1 2 2 2 2 2 1 2 2 1 2 2 1 1 3 3 2 3 2 3 1 2 2 1
#  [519] 3 1 2 3 3 1 1 2 2 1 2 2 3 2 2 2 1 1 2 1 2 1 2 1 2 2 2 1 3 2 1 1 3 1 2 2 1
#  [556] 3 2 3 1 2 1 2 2 2 3 2 2 1 2 1 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 3 1 3
#  [593] 2 2 1 2 3 3 1 1 2 2 1 2 2 2 1 2 2 2 2 2 1 2 1 1 1 1 2 1 1 1 1 2 2 3 2 2 1
#  [630] 2 2 2 3 2 2 2 2 3 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 1 1 2 2 2 2 2 2 1 2
#  [667] 2 2 1 2 2 2 2 2 2 1 2 2 3 3 2 1 1 1 2 1 2 2 1 1 2 2 1 1 2 2 2 2 2 2 1 3 1
#  [704] 2 3 2 1 2 1 2 2 3 2 2 1 1 3 2 1 2 2 2 2 3 1 1 2 3 1 2 2 1 3 2 2 3 1 3 2 2
#  [741] 2 2 2 2 2 2 3 2 2 1 2 2 2 2 2 2 2 1 2 2 2 2 2 1 1 2 1 2 2 2 1 2 2 1 2 1 2
#  [778] 2 2 3 1 2 2 2 2 2 2 3 2 2 2 2 1 3 2 2 1 2 1 1 2 2 2 2 2 1 1 2 1 2 1 2 1 3
#  [815] 2 2 2 2 1 2 2 1 1 1 1 1 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 1 2 1 2 2 1 1 1 1 2
#  [852] 2 2 1 1 3 3 2 1 1 2 1 1 1 2 3 2 2 1 2 2 2 2 1 2 2 1 2 2 2 2 2 1 2 2 2 2 2
#  [889] 2 2 1 1 2 2 1 2 2 1 1 2 2 2 2 2 2 1 2 2 1 2 2 2 2 1 1 2 2 2 1 2 3 1 1 2 3
#  [926] 1 1 2 2 1 2 2 2 2 3 2 2 1 3 2 2 1 2 2 2 2 2 2 2 2 2 1 2 1 2 1 2 2 1 2 2 2
#  [963] 2 2 2 2 1 2 2 2 2 2 2 3 1 1 2 2 2 1 2 2 1 1 1 2 2 1 2 2 2 2 1 2 2 2 2 2 2
# [1000] 2 2 3 2 2 2 2 2 2 2 2 1 2 2 2 2 1 2 2 2 3 1 1 2 3 2 3 2 2 3 2 1 1 2 3 2 2
# [1037] 2 2 2 2 2 2 2 3 1 2 3 2 1 2 2 1 2 1 2 1 1 2 2 2 2 2 1 2 2 2 2 2 2 3 2 2 3
# [1074] 1 3 3 2 1 3 2 2 2 3 1 2 3 1 1 1 1 1 2 2 3 2 1 2 2 2 1 2 3 3 2 1 2 3 2 3 3
# [1111] 3 1 2 1 2 1 1 2 1 1 1 1 2 1 2 1 2 1 2 1 1 1 2 2 1 1 1 1 1 2 2 1 2 2 1 2 2
# [1148] 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 2 1 1 1 2 2 2 2 2 2 1 2 2 2 1 2 1 2 1 1 1 1
# [1185] 2 1 2 1 1 1 1 1 1 1 2 2 2 1 2 2 2 1 1 2 2 2 1 1 2 2 1 2 1 1 1 1 2 2 1 2 2
# [1222] 2 2 2 2 1 1 1 1 2 2 1 2 2 2 2 1 2 2 2 2 2 2 1 1 2 2 2 1 1 2 2 2 1 1 2 1 2
# [1259] 2 2 2 2
# 
# Within cluster sum of squares by cluster:
# [1] 4967.123 5371.726 4498.727
#  (between_SS / total_SS =  38.1 %)
# 
# Available components:
# 
#  [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
#  [6] "betweenss"    "size"         "iter"         "ifault"       "data"

Récupérons les groupes dans zoob

augment(zoo_kmn, zoo) %>.%
  srename(., cluster = .cluster) ->
  zoob

Et enfin, effectuons un graphique similaire à celui réalisé pour la CAH au module précédent. À noter que nous pouvons ici choisir n’importe quelle paire de variables quantitatives pour représenter le nuage de points. Nous ajoutons des ellipses pour matérialiser les groupes à l’aide de stat_ellipse(). Elles contiennent 95% des points du groupe à l’exclusion des extrêmes. Enfin, comme il y a beaucoup de points, nous choisissons de les rendre semi-transparents avec l’argument alpha = 0.2 pour plus de lisibilité du graphique.

chart(zoo_kmn, choices = c("ecd", "compactness"), alpha = 0.2) +
  labs(x = "ECD standardisée", y = "Compacité standardisée") +
  stat_ellipse()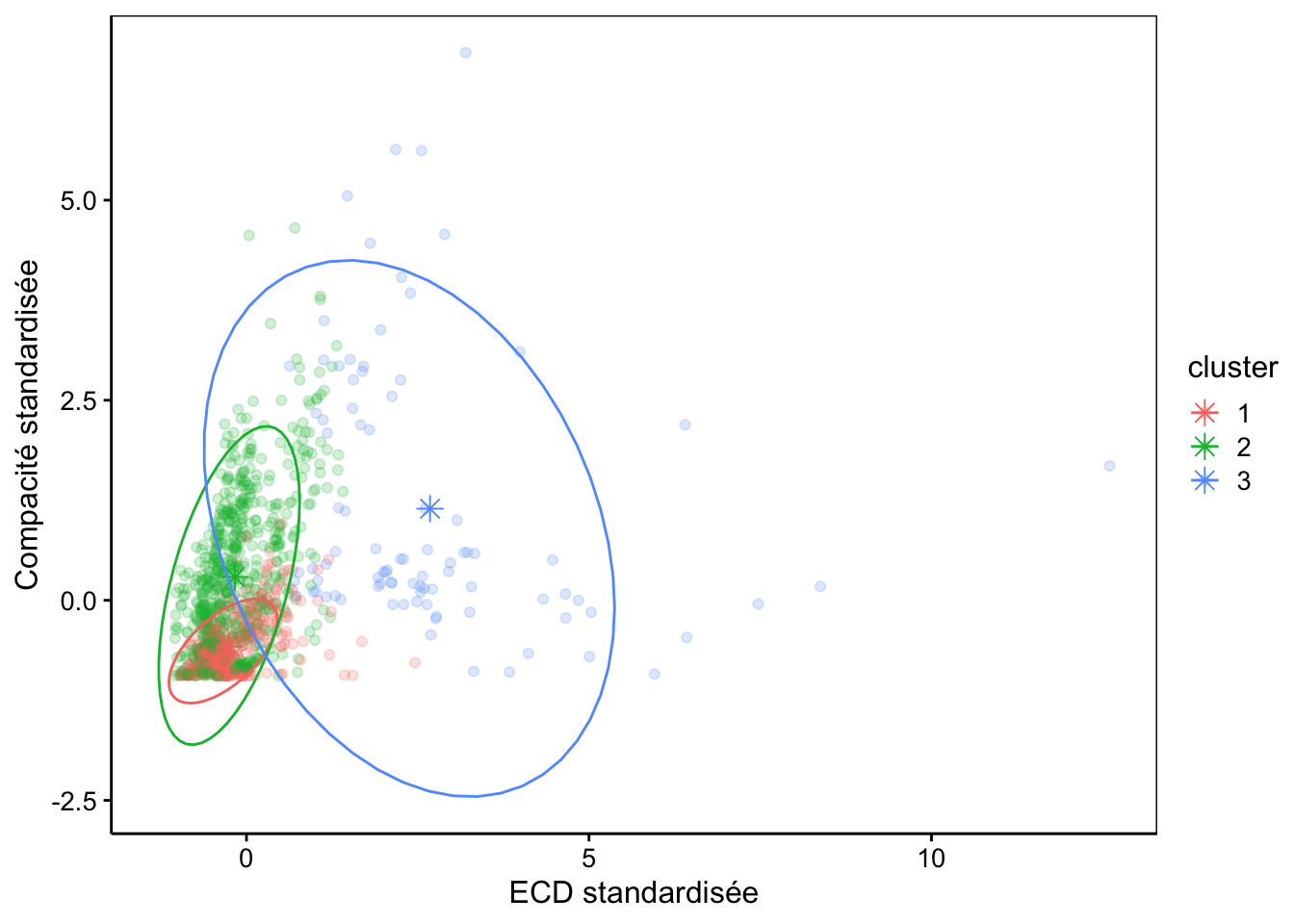

Nous observons ici un regroupement similaire, mais pas identique à la CAH. La tabulation des groupes en fonction des classes connues par ailleurs montre aussi que les k-moyennes donnent des résultats similaires à la CAH :

table(zoob$class, zoob$cluster)

#                   
#                      1   2   3
#   Annelid           39   8   3
#   Appendicularian    1  34   1
#   Calanoid          30 257   1
#   Chaetognath        0   6  45
#   Cirriped           3  19   0
#   Cladoceran        50   0   0
#   Cnidarian          1   9  12
#   Cyclopoid          0  50   0
#   Decapod          126   0   0
#   Egg_elongated      9  41   0
#   Egg_round         37   9   3
#   Fish              43   7   0
#   Gastropod         50   0   0
#   Harpacticoid       0  39   0
#   Malacostracan     49  47  25
#   Poecilostomatoid  73  85   0
#   Protist            0  50   0

Le groupe 1 est également dominé par les annélides, les cladocères, les décapodes, les œufs ronds et les gastéropodes comme pour la CAH. Par contre, on y retrouve aussi la majorité de poissons alors que ces derniers sont dans le second groupe pour la CAH. Le groupe 2 contient majoritairement les copépodes (calanoïdes, cyclopoïdes et poecilostomatoïdes, ce dernier dans une moindre mesure), ainsi que les appendiculaires, les cirripèdes, les œufs allongés et les protistes, comme pour la CAH. Par contre, les malacostracés sont bien plus répartis entre les trois groupes. Enfin, le groupe 3 contient une majorité de chaetognathes et de cnidaires comme pour la CAH.

À vous de jouer !

Pour en savoir plus

Il existe une approche mixte qui combine la CAH et les k-moyennes. Cette approche est intéressante pour les gros jeux de données. Elle est implémentée dans la fonction factoextra::hkmeans() et son utilisation est détaillée ici (en anglais).

Cet article explique dans le détail kmeans() et hclust() dans R, et montre aussi comment on peut calculer les k-moyennes à la main pour bien en comprendre la logique (en anglais).

À vous de jouer !

Effectuez maintenant les exercices du tutoriel B06Lb_kmeans (Partitionnement par k-moyennes).

BioDataScience2::run("B06Lb_kmeans")

Réalisez le travail B06Ia_fish_market, partie II.

Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques II à l’UMONS (Q2 : analyse) à terminer avant le 2025-02-10 23:59:59.

Initiez votre projet GitHub Classroom

Voyez les explications dans le fichier README.md, partie II.

Différents algorithmes avec diverses optimisations existent. Le plus récent et le plus sophistiqué est celui de Hartigan-Wong. Il est utilisé par défaut par la fonction k_means(). En pratique, il y a peu de raison d’en changer.↩︎
Utilisez l’aide en ligne de ?kmeans pour connaître les arguments. Seul centers = est changé en k = dans k_means(), mais avec centers = aussi accepté.↩︎
De manière générale, éviter de rajouter des données calculées dans le jeu de données initial. Cela peut amener à des erreurs particulièrement délicates si vous relancez ensuite l’analyse sur ce tableau.↩︎