2.2 Régression linéaire multiple
Dans le cas de la régression linéaire simple, nous considérions le modèle statistique suivant (avec \(\epsilon\) représentant les résidus, terme statistique dans l’équation) :
\[y = a \ x + b + \epsilon \]
Dans le cas de la régression linéaire multiple, nous introduirons plusieurs variables indépendantes notés \(x_1\), \(x_2\), …, \(x_n\) :
\[y = a_1 \ x_1 + a_2 \ x_2 + ... + a_n \ x_n + b + \epsilon \]
La bonne nouvelle, c’est que tous les calculs, les métriques et les tests d’hypothèses relatifs à la régression linéaire simple se généralisent simplement et naturellement, tout comme nous sommes passés dans le cours SDD 1 de l’ANOVA à 1 facteur à un modèle plus complexe à 2 ou plusieurs facteurs. Voyons tout de suite ce que cela donne si nous voulions utiliser à la fois le diamètre et la hauteur des cerisiers noirs pour prédire leur volume de bois :
#
# Call:
# lm(formula = volume ~ diameter + height, data = trees)
#
# Residuals:
# Min 1Q Median 3Q Max
# -0.180423 -0.074919 -0.006874 0.062244 0.241801
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -1.63563 0.24462 -6.686 2.95e-07 ***
# diameter 5.25643 0.29594 17.762 < 2e-16 ***
# height 0.03112 0.01209 2.574 0.0156 *
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# Residual standard error: 0.1104 on 28 degrees of freedom
# Multiple R-squared: 0.9475, Adjusted R-squared: 0.9438
# F-statistic: 252.7 on 2 and 28 DF, p-value: < 2.2e-16D’un point de vue pratique, nous voyons que la formule qui spécifie le modèle peut très bien comporter plusieurs variables séparées par des +. Nous avons ici trois paramètres dans notre modèle : l’ordonnée à l’origine qui vaut -1,63, la pente relative au diamètre de 5,25, et la pente relative à la hauteur de 0,031. Le modèle lm2 sera donc paramétré comme suit : volume de bois = 5,25 . diamètre + 0,031 . hauteur - 1,63.
Notons que la pente relative à la hauteur (0,031) n’est pas significativement différente de zéro au seuil \(\alpha\) de 1% (mais l’est seulement pour \(\alpha\) = 5%). En effet, la valeur t du test de Student associé (H0 : le paramètre vaut zéro, H1 : le paramètre est différent de zéro) vaut 2,574. Cela correspond à une valeur p du test de 0,0156, une valeur moyennement significative donc, matérialisée par une seule astérisque à la droite du tableau. Cela dénote un plus faible pouvoir de prédiction du volume de bois via la hauteur que via le diamètre de l’arbre. Nous l’avions déjà observé sur le graphique matrice de nuages de points réalisé initialement, ainsi que via les coefficients de corrélation respectifs.
La représentation de cette régression nécessite un graphique à trois dimensions (diamètre, hauteur et volume) et le modèle représente en fait le meilleur plan dans cet espace à 3 dimensions. Pour un modèle comportant plus de deux variables indépendantes, il n’est plus possible de représenter graphiquement la régression.
car::scatter3d(data = trees, volume ~ diameter + height, fit = "linear",
residuals = TRUE, bg = "white", axis.scales = TRUE, grid = TRUE,
ellipsoid = FALSE)
rgl::rglwidget(width = 800, height = 800)Utilisez la souris pour zoomer (molette) et pour retourner le graphique (cliquez et déplacer la souris en maintenant le bouton enfoncé) pour comprendre ce graphique 3D. La régression est matérialisée par un plan en bleu. Les observations sont les boules jaunes et les résidus sont des traits cyans lorsqu’ils sont positifs et magenta lorsqu’ils sont négatifs.
Les graphes d’analyse des résidus sont toujours disponibles (nous ne représentons ici que les quatre premiers) :
#plot(lm2, which = 1)
lm2 %>.%
chart(broom::augment(.), .resid ~ .fitted) +
geom_point() +
geom_hline(yintercept = 0) +
geom_smooth(se = FALSE, method = "loess", formula = y ~ x) +
labs(x = "Fitted values", y = "Residuals") +
ggtitle("Residuals vs Fitted") 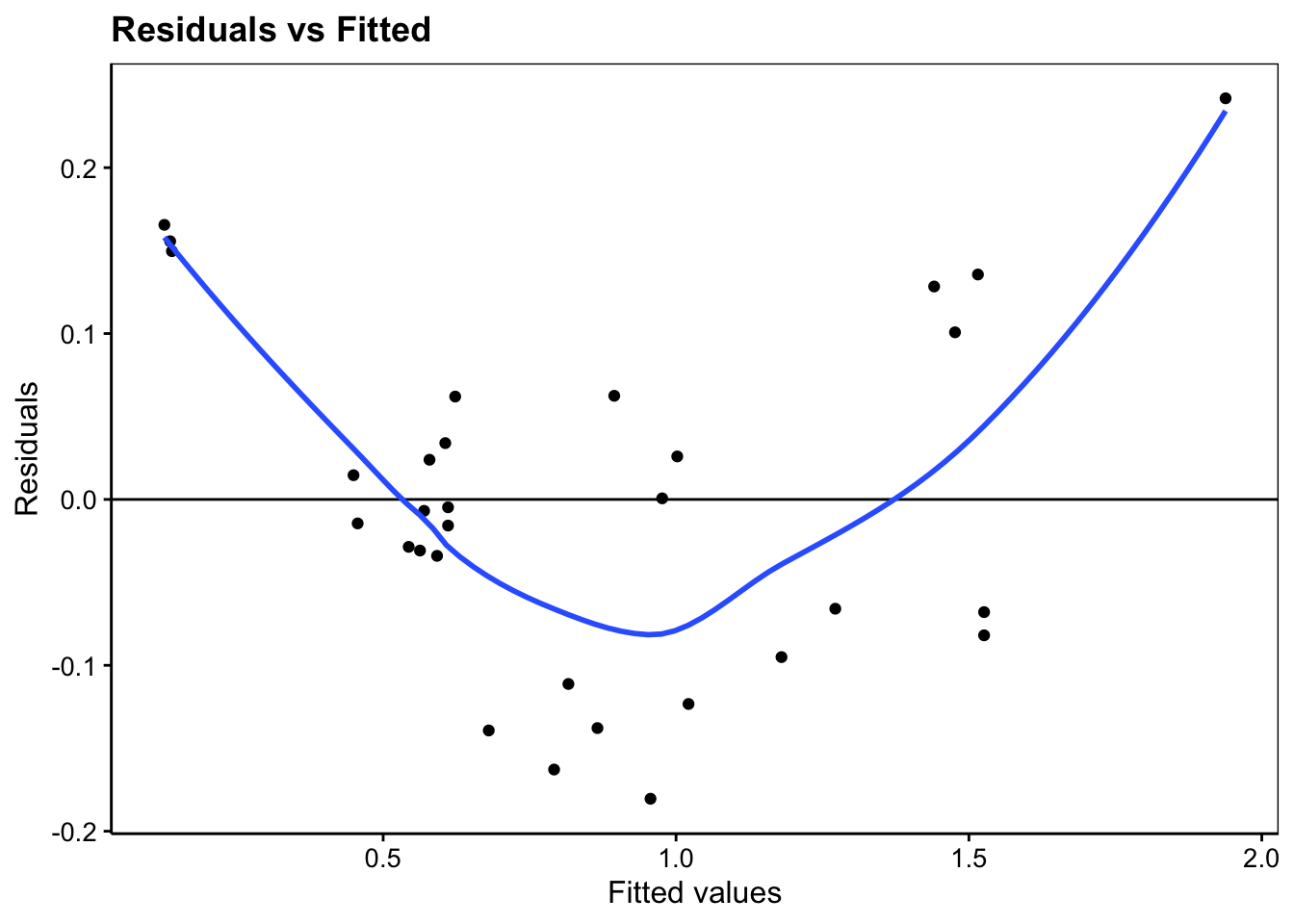
#plot(lm2, which = 2)
lm2 %>.%
chart(broom::augment(.), aes(sample = .std.resid)) +
geom_qq() +
geom_qq_line(colour = "darkgray") +
labs(x = "Theoretical quantiles", y = "Standardized residuals") +
ggtitle("Normal Q-Q") 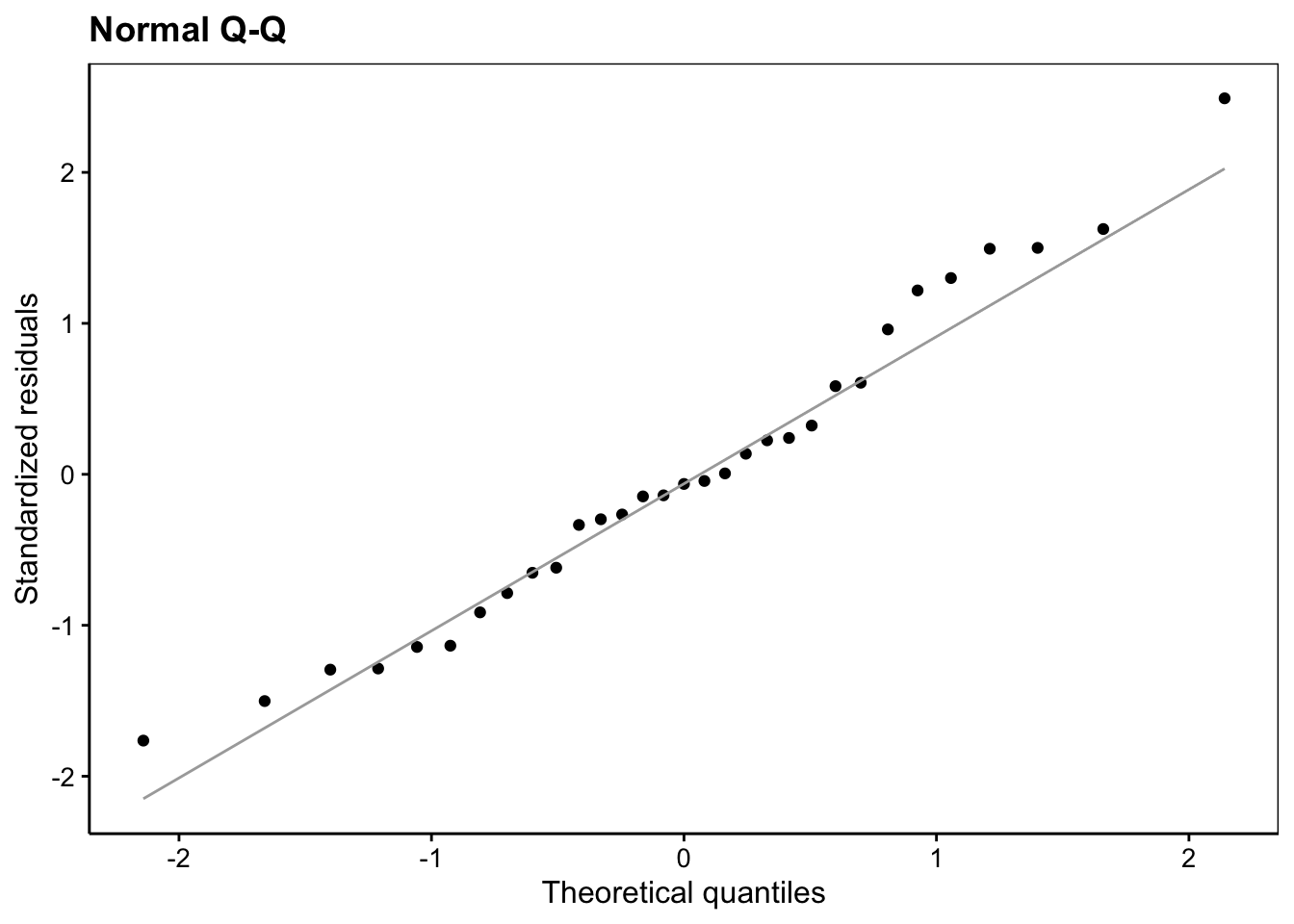
#plot(lm2, which = 3)
lm2 %>.%
chart(broom::augment(.), sqrt(abs(.std.resid)) ~ .fitted) +
geom_point() +
geom_smooth(se = FALSE, method = "loess", formula = y ~ x) +
labs(x = "Fitted values",
y = expression(bold(sqrt(abs("Standardized residuals"))))) +
ggtitle("Scale-Location") 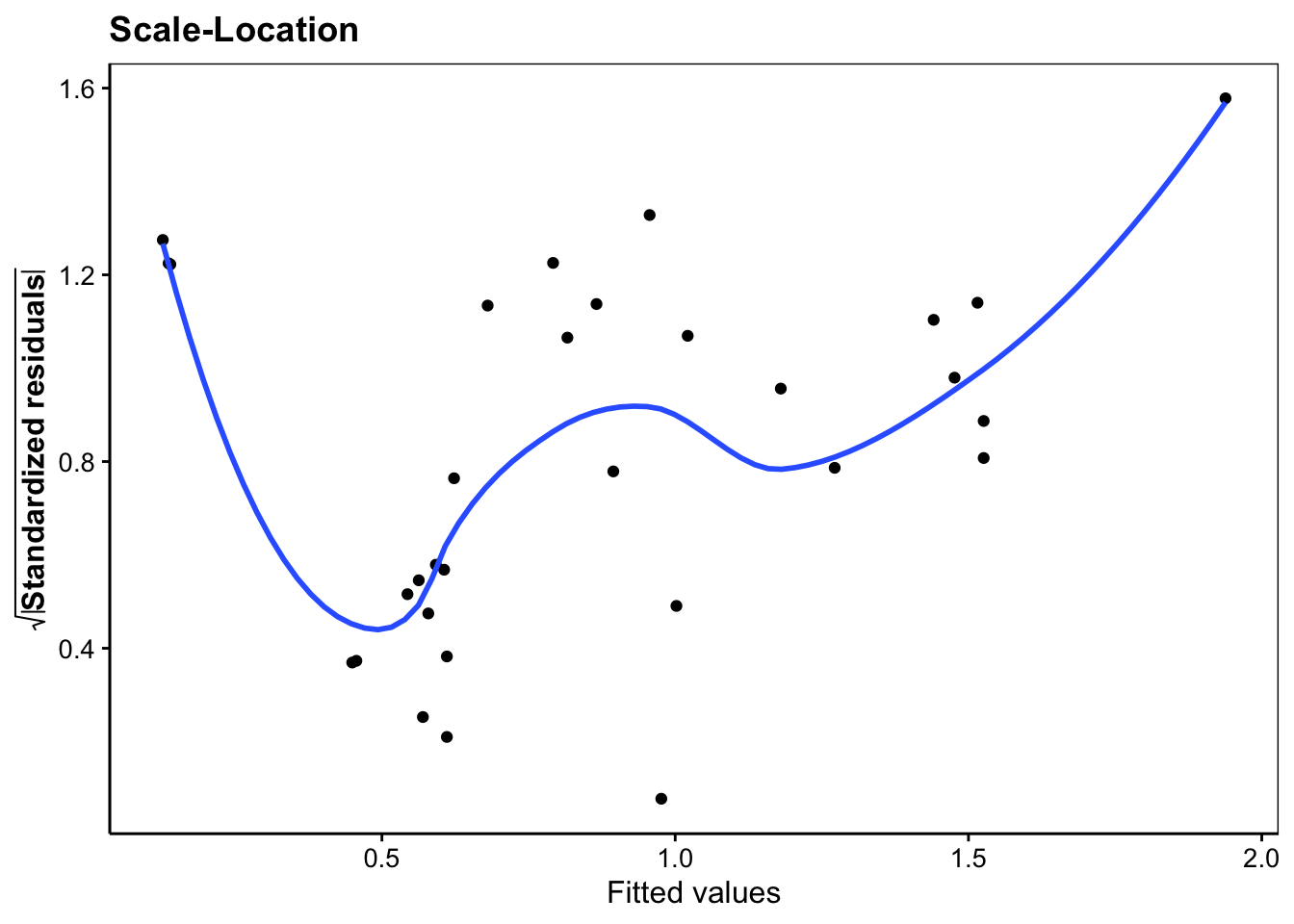
#plot(lm2, which = 4)
lm2 %>.%
chart(broom::augment(.), .cooksd ~ seq_along(.cooksd)) +
geom_bar(stat = "identity") +
geom_hline(yintercept = seq(0, 0.1, by = 0.05), colour = "darkgray") +
labs(x = "Obs. number", y = "Cook's distance") +
ggtitle("Cook's distance") 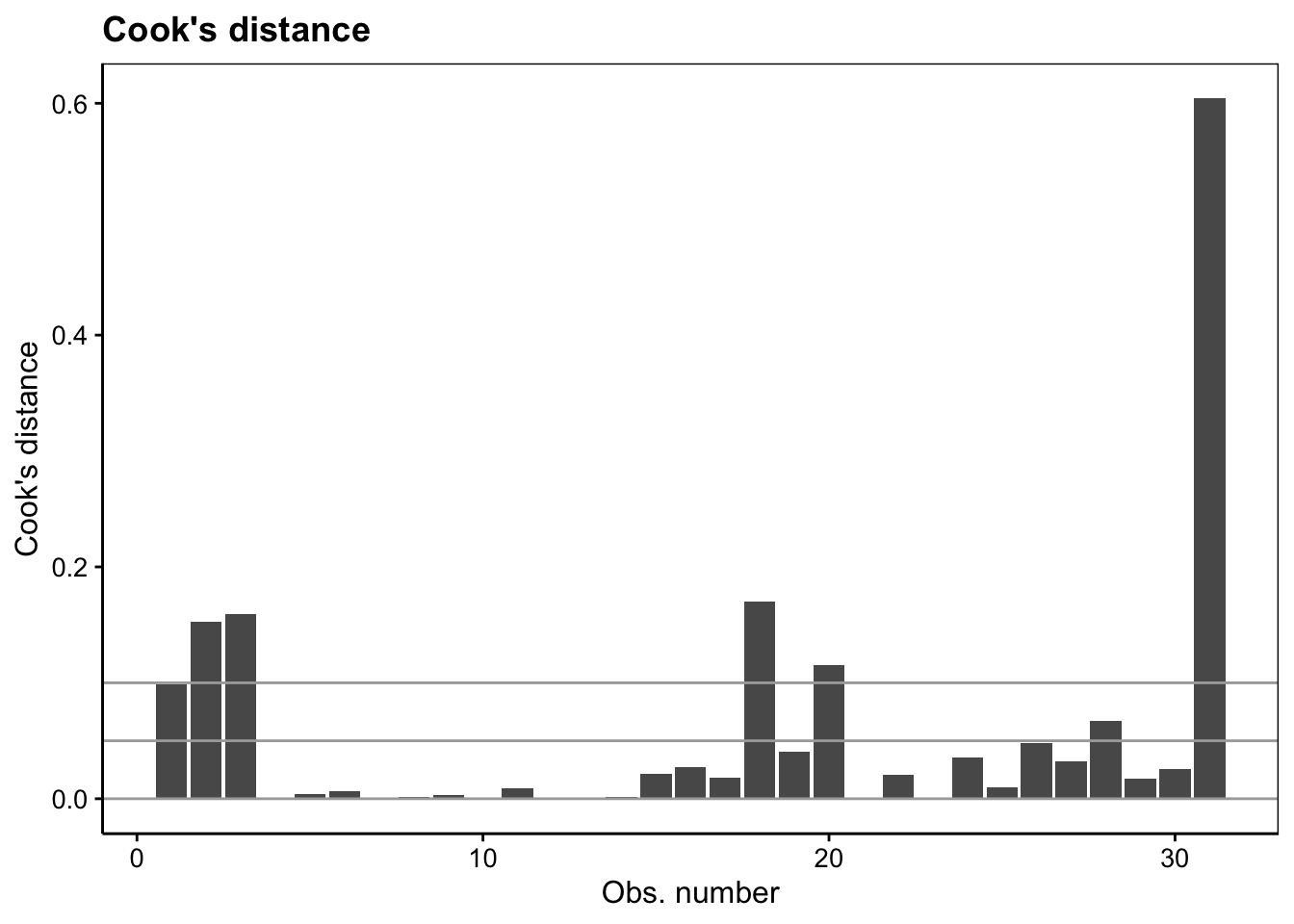
Est-ce que ce modèle est préférable à celui n’utilisant que le diamètre ? Le R2 ajusté est passé de 0,933 avec le modèle simple lm. utilisant uniquement le diamètre à 0,944 dans le présent modèle lm2 utilisant le diamètre et la hauteur. Cela semble une amélioration, mais le test de significativité de la pente pour la hauteur ne nous indique pas un résultat très significatif. De plus, cela a un coût en pratique de devoir mesurer deux variables au lieu d’une seule pour estimer le volume de bois. Cela en vaut-il la peine ? Nous sommes encore une fois confrontés à la question de comparer deux modèles, cette fois-ci ayant une complexité croissante.
Dans le cas particulier de modèles imbriqués (un modèle contient l’autre, mais rajoute un ou plusieurs termes), une ANOVA est possible en décomposant la variance selon les composantes reprises respectivement par chacun des deux modèles. La fonction anova() est programmée pour faire ce calcul en lui indiquant chacun des deux objets contenant les modèles à comparer :
# Analysis of Variance Table
#
# Model 1: volume ~ diameter
# Model 2: volume ~ diameter + height
# Res.Df RSS Df Sum of Sq F Pr(>F)
# 1 29 0.42176
# 2 28 0.34104 1 0.080721 6.6274 0.01562 *
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Notez que dans le cas de l’ajout d’un seul terme, la valeur p de cette ANOVA est identique à la valeur p de test de significativité du paramètre (ici, cette valeur p est de 0,0156 dans les deux cas). Donc, le choix peut se faire directement à partir de summary() pour ce terme unique. La conclusion est similaire : l’ANOVA donne un résultat seulement moyennement significatif entre les 2 modèles. Dans un cas plus complexe, la fonction anova() de comparaison pourra être utile. Enfin, tous les modèles ne sont pas nécessairement imbriqués. Dans ce cas, il nous faudra un autre moyen de les départager, … mais avant d’aborder cela, étudions une variante intéressante de la régression multiple : la régression polynomiale.
À vous de jouer !
Effectuez maintenant les exercices du tutoriel B02La_reg_multi (Régression linéaire multiple).
BioDataScience2::run("B02La_reg_multi")