7.1 Analyse en composantes principales
Notre première approche d’ordination avec le MDS dans le précédent module nous a permis de comprendre l’intérêt de représenter des données multivariées sur des cartes. Malheureusement, les techniques itératives et basées sur les matrices de distances du MDS rendent cette technique peu propice pour analyser des gros jeux de données. En effet, le temps de calcul et le besoin en mémoire vive grandissent de manière exponentielle avec la taille des jeux de données. Heureusement, il existe aussi des techniques d’ordination qui se calculent plus facilement et plus rapidement sur de très gros jeux de données. L’Analyse en Composantes Principales ou ACP (Principal Component Analysis ou PCA en anglais) est une méthode de base qu’il est indispensable de connaître et de comprendre. La plupart des autres techniques d’ordination plus sophistiquées sont des variante de l’ACP.
Des relations linéaires sont suspectées entres les variables (si elles ne sont pas linéaires, penser à transformer les données auparavant pour les linéariser).
Ces relations conduisent à une répartition des individus (le nuage de points) qui forme une structure que l’on cherchera à interpréter.
Pour visualiser cette structure, les données sont simplifiées (réduites) de N variables à n (n < N et n = 2 ou 3 généralement). La représentation sous forme d’un nuage de points s’appelle une carte.
La réduction des dimensions se fait avec une perte minimale d’information au sens de la variance des données.
7.1.1 ACP dans SciViews::R
L’ACP est facilitée dans SciViews::R, mais au stade actuel, tout le code nécessaire (en particulier pour réaliser les graphiques avec chart()) n’est pas encore complètement intégré dans les packages. Ainsi, vous pouvez copier-coller le code du chunk suivant au début de vos scripts ou dans un chunk de setup dans vos documents R Markdown/Notebook (cliquez sur “voir le code” pour le dérouler).
7.1.2 Indiens diabétiques
Les indiens Pimas sont des amérindiens originaires du nord du Mexique qui sont connus pour compter le plus haut pourcentage d’obèses et de diabétiques de toutes les ethnies. Ils ont fait l’objet de plusieurs études scientifiques d’autant plus que les Pimas en Arizona développent principalement cette obésité et ce diabète, alors que les Pimas mexicains les ont plus rarement. Il est supposé que leur mode de vie différent aux États-Unis pourrait en être la raison. Voici un jeu de données qui permet d’explorer un peu ceci :
# # A tibble: 768 x 9
# pregnant glucose pressure triceps insulin mass pedigree age diabetes
# <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <fct>
# 1 6 148 72 35 NA 33.6 0.627 50 pos
# 2 1 85 66 29 NA 26.6 0.351 31 neg
# 3 8 183 64 NA NA 23.3 0.672 32 pos
# 4 1 89 66 23 94 28.1 0.167 21 neg
# 5 0 137 40 35 168 43.1 2.29 33 pos
# 6 5 116 74 NA NA 25.6 0.201 30 neg
# 7 3 78 50 32 88 31 0.248 26 pos
# 8 10 115 NA NA NA 35.3 0.134 29 neg
# 9 2 197 70 45 543 30.5 0.158 53 pos
# 10 8 125 96 NA NA NA 0.232 54 pos
# # … with 758 more rowsCe jeu de données contient des valeurs manquantes. Le graphique suivant permet de visualiser l’importance des “dégâts” :
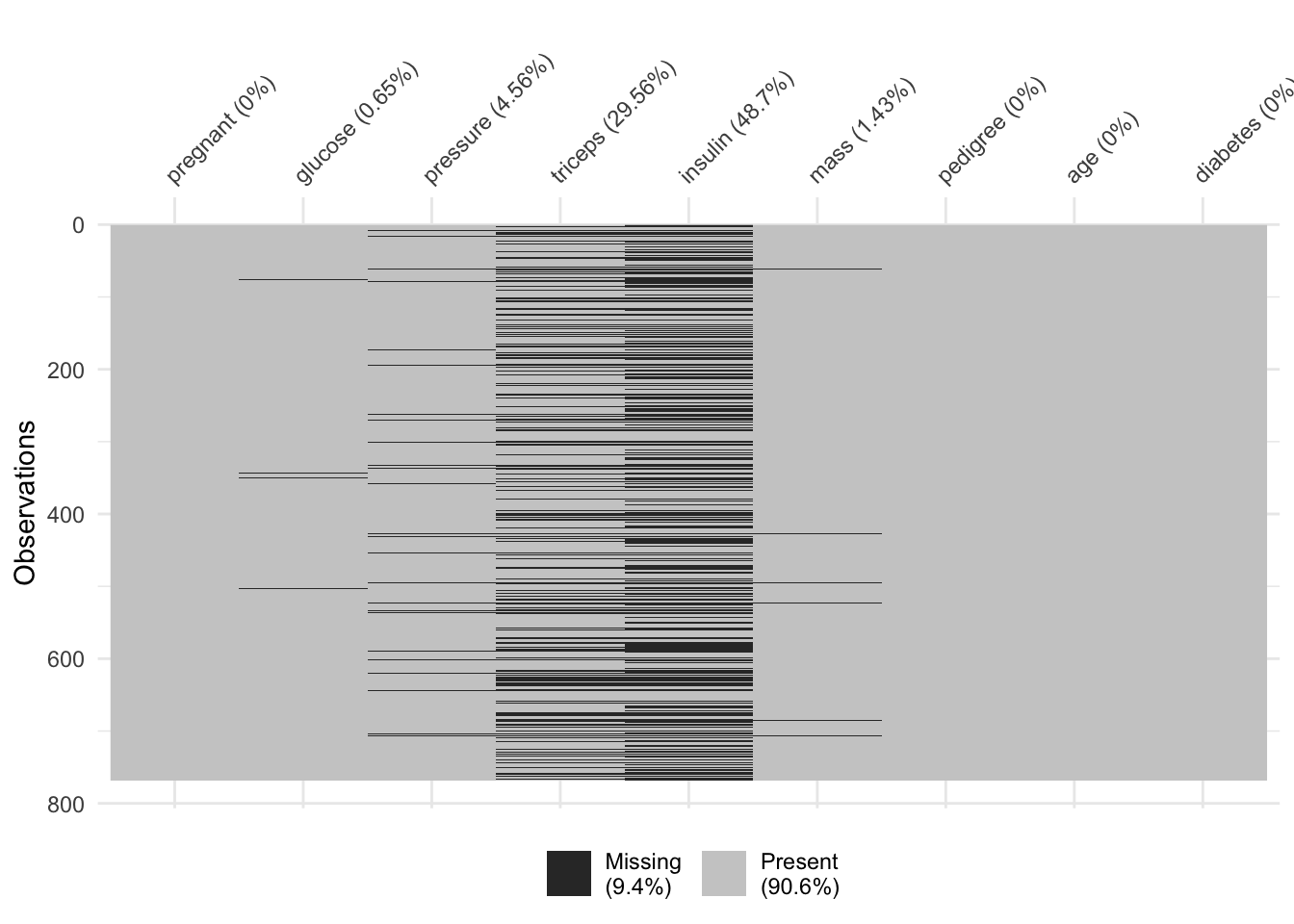
Moins de 10% des données sont manquantes, et c’est principalement dans les variables insulin et triceps. Si nous souhaitons un tableau sans variables manquantes, nous pouvons décider d’éliminer des lignes et ou des colonnes (variables), mais ici nous souhaitons garder toutes les variables et réduisons donc uniquement le nombre de lignes avec la fonction drop_na().
# # A tibble: 392 x 9
# pregnant glucose pressure triceps insulin mass pedigree age diabetes
# <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <fct>
# 1 1 89 66 23 94 28.1 0.167 21 neg
# 2 0 137 40 35 168 43.1 2.29 33 pos
# 3 3 78 50 32 88 31 0.248 26 pos
# 4 2 197 70 45 543 30.5 0.158 53 pos
# 5 1 189 60 23 846 30.1 0.398 59 pos
# 6 5 166 72 19 175 25.8 0.587 51 pos
# 7 0 118 84 47 230 45.8 0.551 31 pos
# 8 1 103 30 38 83 43.3 0.183 33 neg
# 9 1 115 70 30 96 34.6 0.529 32 pos
# 10 3 126 88 41 235 39.3 0.704 27 neg
# # … with 382 more rowsAvant de nous lancer dans une ACP, nous devons décrire les données, repérer les variables quantitatives d’intérêt, et synthétiser les corrélations linéaires (coefficients de corrélation de Pearson) entre ces variables.
| Name | pima |
| Number of rows | 392 |
| Number of columns | 9 |
| _______________________ | |
| Column type frequency: | |
| factor | 1 |
| numeric | 8 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| diabetes | 0 | 1 | FALSE | 2 | neg: 262, pos: 130 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| pregnant | 0 | 1 | 3.30 | 3.21 | 0.00 | 1.00 | 2.00 | 5.00 | 17.00 | ▇▂▂▁▁ |
| glucose | 0 | 1 | 122.63 | 30.86 | 56.00 | 99.00 | 119.00 | 143.00 | 198.00 | ▂▇▇▃▂ |
| pressure | 0 | 1 | 70.66 | 12.50 | 24.00 | 62.00 | 70.00 | 78.00 | 110.00 | ▁▂▇▆▁ |
| triceps | 0 | 1 | 29.15 | 10.52 | 7.00 | 21.00 | 29.00 | 37.00 | 63.00 | ▅▇▇▃▁ |
| insulin | 0 | 1 | 156.06 | 118.84 | 14.00 | 76.75 | 125.50 | 190.00 | 846.00 | ▇▂▁▁▁ |
| mass | 0 | 1 | 33.09 | 7.03 | 18.20 | 28.40 | 33.20 | 37.10 | 67.10 | ▃▇▃▁▁ |
| pedigree | 0 | 1 | 0.52 | 0.35 | 0.09 | 0.27 | 0.45 | 0.69 | 2.42 | ▇▃▁▁▁ |
| age | 0 | 1 | 30.86 | 10.20 | 21.00 | 23.00 | 27.00 | 36.00 | 81.00 | ▇▂▁▁▁ |
Nous avons une variable facteur diabetes à exclure de l’analyse, mais la variable pregnant, est une variable numérique discrète (nombre d’enfants portés). Nous l’éliminerons aussi de l’analyse.
La fonction correlation() du package SciViews nous permet d’inspecter les corrélations entre les variables choisies (donc toutes à l’exception de pregnant et diabetes qui ne sont pas quantitatives continues) :
| glucose | pressure | triceps | insulin | mass | pedigree | age | |
|---|---|---|---|---|---|---|---|
| glucose | 1.00 | 0.21 | 0.20 | 0.58 | 0.21 | 0.14 | 0.34 |
| pressure | 0.21 | 1.00 | 0.23 | 0.10 | 0.30 | -0.02 | 0.30 |
| triceps | 0.20 | 0.23 | 1.00 | 0.18 | 0.66 | 0.16 | 0.17 |
| insulin | 0.58 | 0.10 | 0.18 | 1.00 | 0.23 | 0.14 | 0.22 |
| mass | 0.21 | 0.30 | 0.66 | 0.23 | 1.00 | 0.16 | 0.07 |
| pedigree | 0.14 | -0.02 | 0.16 | 0.14 | 0.16 | 1.00 | 0.09 |
| age | 0.34 | 0.30 | 0.17 | 0.22 | 0.07 | 0.09 | 1.00 |
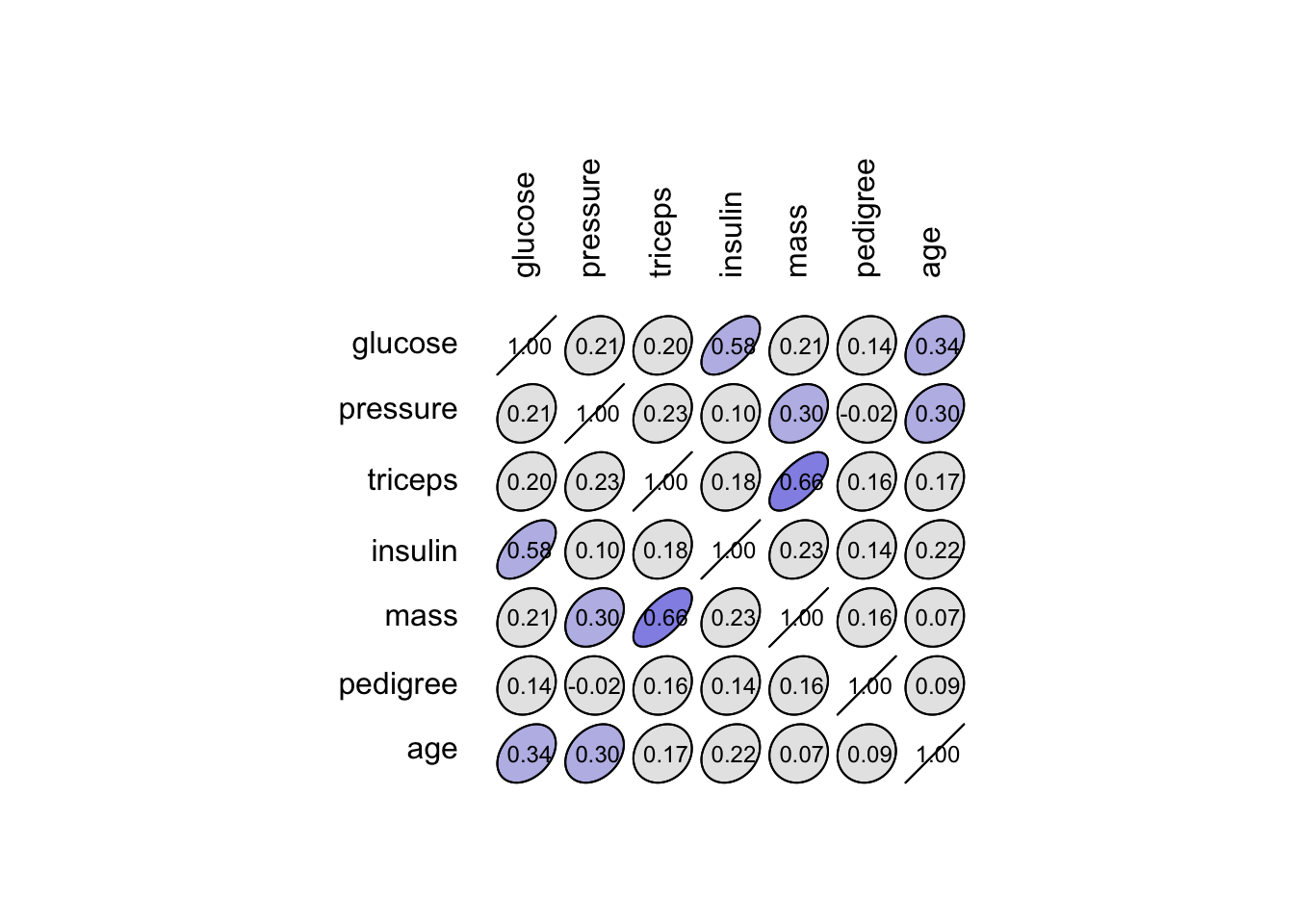
Quelques corrélations positives d’intensités moyennes se dégagent ici, notamment entre mass et triceps (épaisseur du pli cutané au niveau du triceps), ainsi qu’entre glucose (taux de glucose dans le sang), insulin (taux d’insuline dans le sang) et age. Par contre, la pression artérielle (pressure) et le pedigree (variable qui quantifie la susceptibilité au diabète en fonction de la parenté) semblent peu corrélés avec les autres variables.
L’ACP est en fait équivalente à une Analyse en Coordonnées Principales sur une matrice de distances euclidiennes (MDS métrique), mais en plus efficace en terme de calculs. Nous pouvons donc nous lancer dans l’analyse et en comprendre les résultats en gardant ceci à l’esprit.
À vous de jouer !
Nous utiliserons la fonction pca() qui prend un argument data = et une formule du type ~ var1 + var2 + .... + varn, ou plus simplement, directement un tableau contenant uniquement les variables à analyser comme argument unique. Comme les différentes variables sont mesurées dans des unités différentes, nous devons les standardiser (écart type ramené à un pour toutes). Ceci est réalisé par la fonction pca() en lui indiquant scale = TRUE. Donc :
pima_pca <- pca(data = pima, ~ glucose + pressure + triceps + insulin + mass +
pedigree + age, scale = TRUE)Ou alors, nous sélectionnons les variables d’intérêt avec select() et appliquons pca() directement sur ce tableau, ce qui donnera le même résultat.
Le nuage de points dans l’espace initial à sept dimensions a été centré (origine ramenée au centre de gravité du nuage de points = moyenne des variables) par l’ACP. Ensuite une rotation des axes a été réalisée pour orienter son plus grand axe selon un premier axe principal 1 ou PC1 . Ensuite PC2 est construit orthogonal au premier et dans la seconde direction de plus grande variabilité du nuage de points, et ainsi de suite pour les autres axes. Ainsi les axes PC1, PC2, PC3, … représentent une part de variance de plus en plus faible par rapport à la variance totale du jeu de données. Ceci est présenté dans le résumé :
# Importance of components (eigenvalues):
# PC1 PC2 PC3 PC4 PC5 PC6 PC7
# Variance 2.412 1.288 1.074 0.878 0.6389 0.399 0.3098
# Proportion of Variance 0.345 0.184 0.153 0.126 0.0913 0.057 0.0443
# Cumulative Proportion 0.345 0.529 0.682 0.807 0.8988 0.956 1.0000
#
# Loadings (eigenvectors, rotation matrix):
# PC1 PC2 PC3 PC4 PC5 PC6 PC7
# glucose 0.441 -0.455 -0.198 0.736
# pressure 0.329 0.101 -0.613 0.206 0.654 -0.171
# triceps 0.439 0.488 -0.367 -0.644
# insulin 0.402 -0.418 0.263 -0.388 0.123 -0.642 -0.129
# mass 0.446 0.506 -0.181 0.711
# pedigree 0.198 0.625 0.711 0.251
# age 0.325 -0.337 -0.384 0.471 -0.592 -0.168 0.179Le premier tableau Importance of components (eigenvalues): montre la part de variance présentée sur chacun des sept axes de l’ACP (PC1, PC2, …, PC7). Le fait qu’il s’agit de valeurs propres (eigenvalues en anglais) apparaîtra plus clair lorsque vous aurez lu les explications détaillées plus bas. Ces parts de variance s’additionnent pour donner la variance totale du nuage de points dans les sept dimensions (propriété d’additivité des variances). Pour facilité la lecture, la Proportion de Variance en % est reprise également, ainsi que les proportions cumulées. Ainsi, les deux premiers axes de l’ACP capturent ici 53% de la variance totale. Et il faudrait considérer les cinq premiers axes pour capturer 90% de la variance totale. Cependant, les trois premiers axes cumulent tout de même plus des 2/3 de la variance. Nous pouvons restreindre notre analyse à ces trois axes-là.
Le second tableau Loadings (eigenvectors, rotation matrix): est la matrice de transformation des coordonnées initiales sur les lignes en coordonnées PC1 à PC7 en colonnes. Nous pouvons y lire l’importante des variables initiales sur les axes de l’ACP. Par exemple, l’axe PC3 contraste essentiellement pressure et pedigree.
À vous de jouer !
Le graphique des éboulis sert à visualiser la “chute” de la variance d’un axe principal à l’autre, et aide à choisir le nombre d’axes à conserver (espace à dimensions réduites avec perte minimale d’information). Deux variantes en diagramme en barres verticales chart$screeplot() ou chart$scree() ou sous forme d’une ligne brisée chart$altscree() sont disponibles :
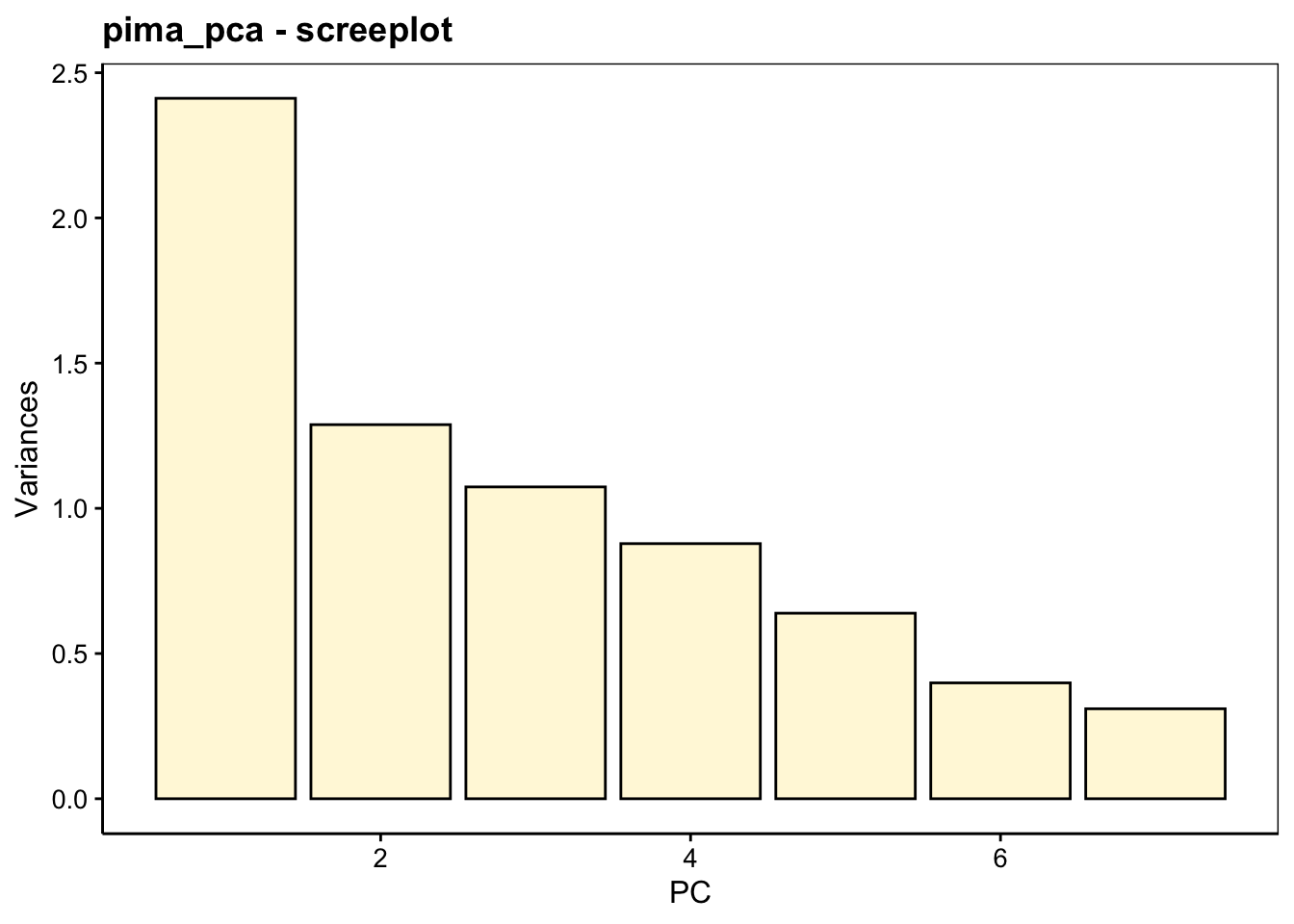
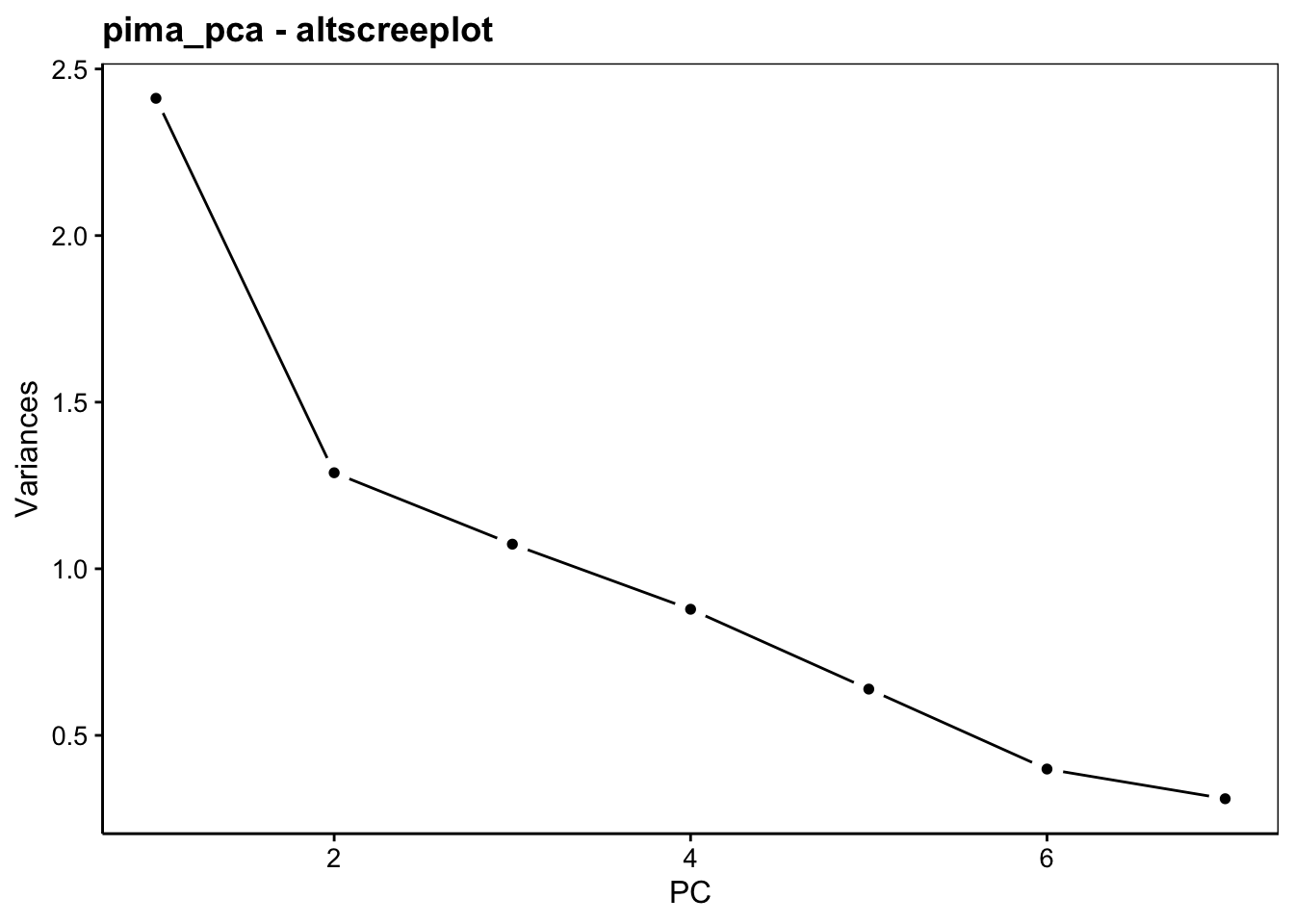
La diminution est importante entre le premier et le second axe, mais plus progressive ensuite. Ceci traduit une structure plus complexe dans les données qui ne se réduit pas facilement à un très petit nombre d’axes. Nous pouvons visualiser le premier plan principal constitué par PC1 et PC2, tout en gardant à l’esprit que seulement 53% de la variance totale y est capturée. Donc, nous pouvons nous attendre à des déformations non négligeables des données dans ce plan, et d’autres aspects qui n’y sont pas (correctement) représentés. Nous verrons qu’il est porteur, toutefois, d’information utile.
À vous de jouer !
Deux types de représentations peuvent être réalisées à partir d’ici : la représentation dans l’espace des variables, et la représentation complémentaire dans l’espace des individus. Ces deux représentations sont complémentaires et s’analysent conjointement. L’espace des variables représente les axes initiaux projetés comme des ombres dans le plan choisi de l’ACP (rappelez-vous l’analogie avec les ombres chinoises). Il se réalise à l’aide de chart$loadings(). Par exemple pour PC1 et PC2 nous indiquons choices = c(1, 2) (ou rien du tout, puisque ce sont les valeurs par défaut)) :
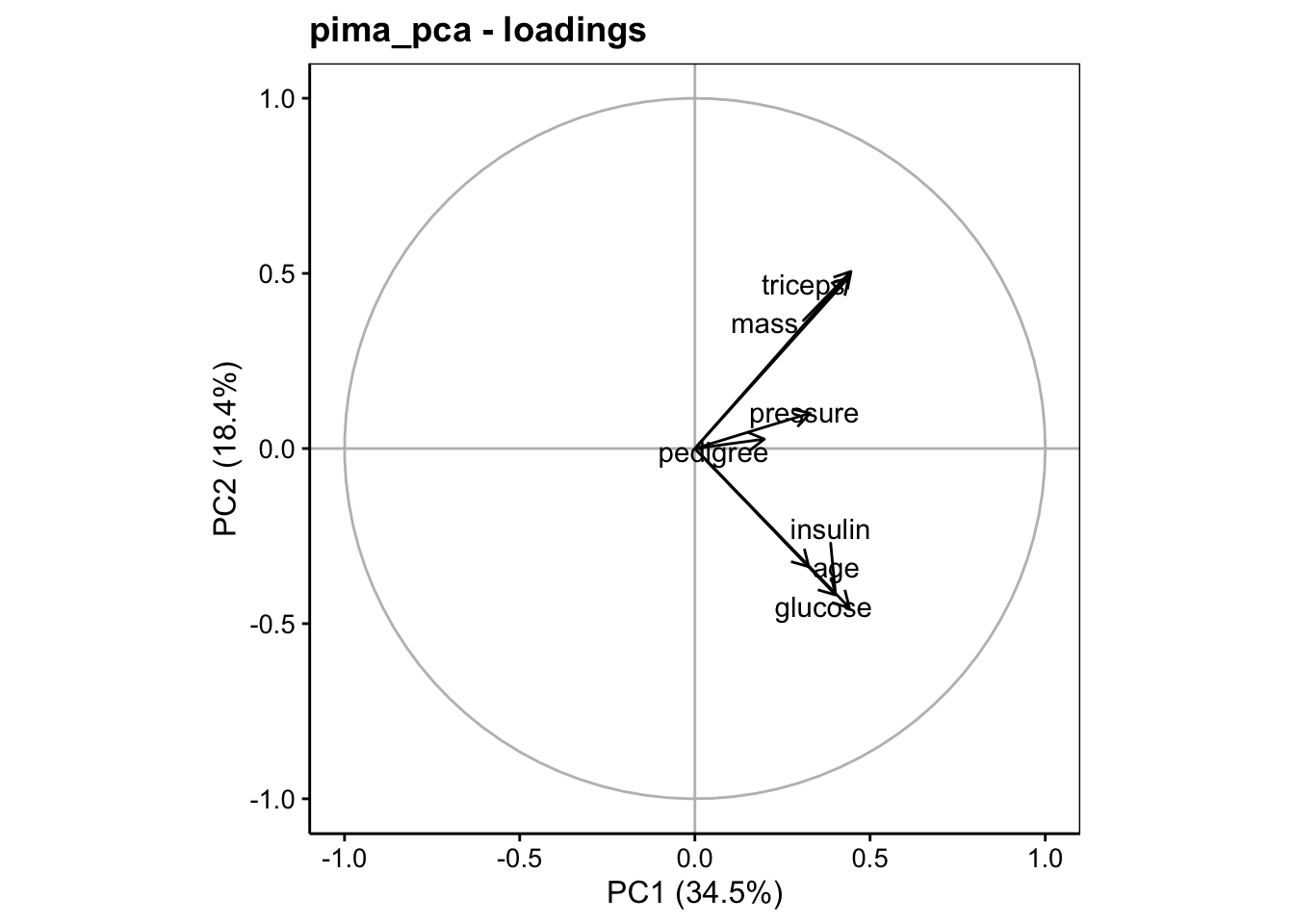
Ce graphique s’interprète comme suit :
Plus la norme (longueur) du vecteur qui représente une variable est grande et se rapproche de un (matérialisé par le cercle gris), plus la variable est bien représentée dans le plan choisi. On évitera d’interpréter ici les variables qui ont des normes petites, comme
pedigreeoupressure.Des vecteurs qui pointent dans la même direction représentent des variables directement corrélés entre elles. C’est le cas de
glucose,insulinetaged’une part, et par ailleurs aussi demassettriceps.Des vecteurs qui pointent en directions opposées représentent des variables inversement proportionnelles. Il n’y en a pas ici.
Des vecteurs orthogonaux représentent des variables non corrélées entre elles. ainsi le groupe
glucose/insulin/agen’est pas corrélé avec le groupemass/tricepsLes PCs sont orientés en fonction des variables initiales, ou à défaut, les zones du graphique sont orientés. Ici, les gros sont dans le haut à droite du graphique, alors que ceux qui sont âgés, et ont beaucoup de sucre et d’insuline dans le sang sont en bas à droite. A l’opposé, on trouve les plus maigres en bas à gauche et les jeunes ayant moins de glucose et d’insuline dans le sang en haut à gauche du graphique.
Cela donne déjà une vision synthétique des différentes corrélations entre la variables. Naturellement, on peut très bien choisir d’autres axes, pour peu qu’ils représentent une part de variance relativement importante. Par exemple, ici, nous pouvons représente le plan constitué par PC1 et PC3, puisque nous avons décidé de retenir les 3 premiers axes :
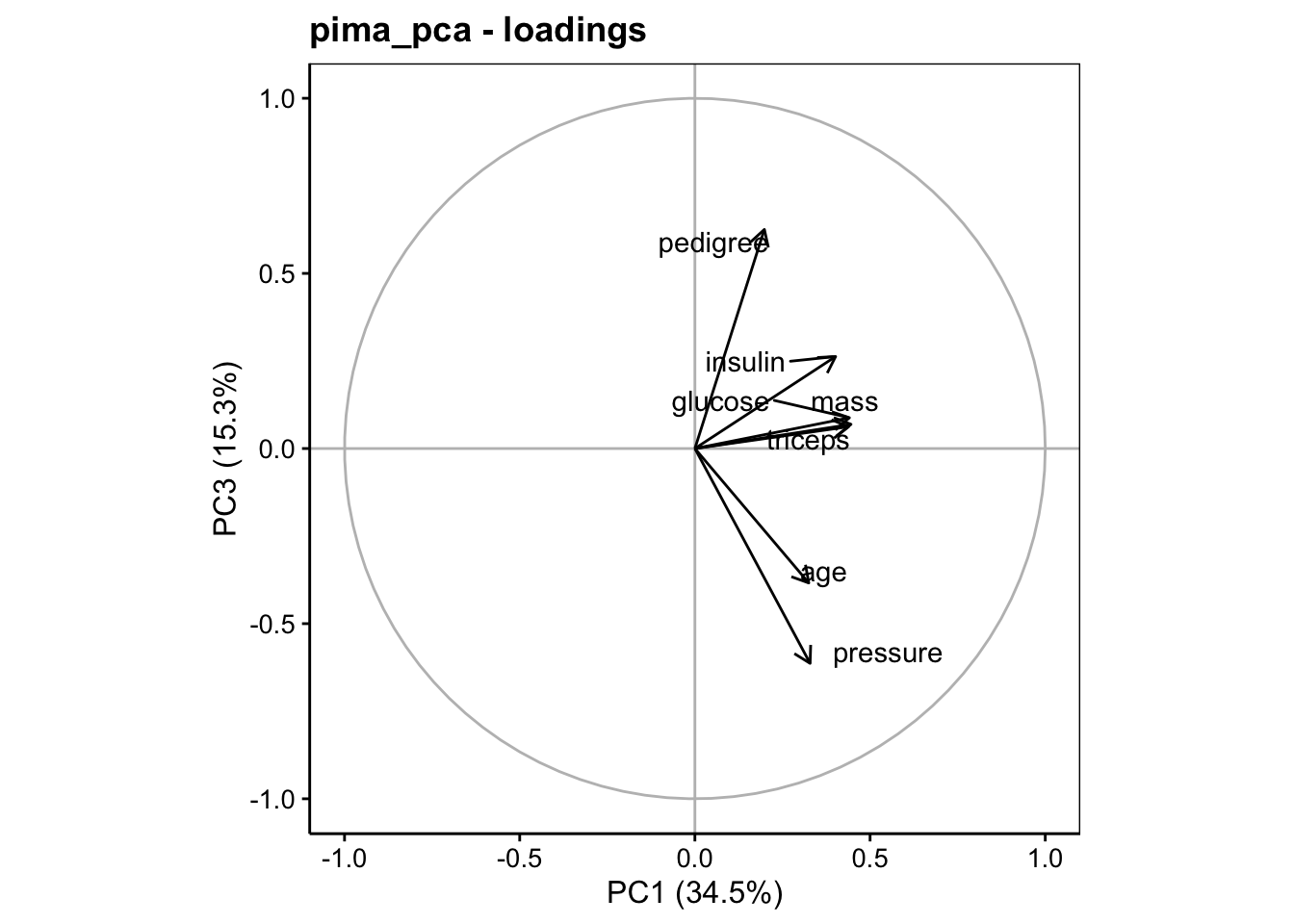
Nous voyons que pedigree et pressure (inversement proportionnels) sont bien mieux représentés le long de PC3. Ici l’axe PC3 est plus facile à orienter : en haut les pedigrees élevés et les pressions artérielles basses, et en bas le contraire. Nous avons déjà lu cette information dans le tableau des vecteurs propres de summary().
Le graphique entre PC2 et PC3 complète l’analyse, mais n’apportant rien de plus, il peut être typiquement éliminé de votre rapport.
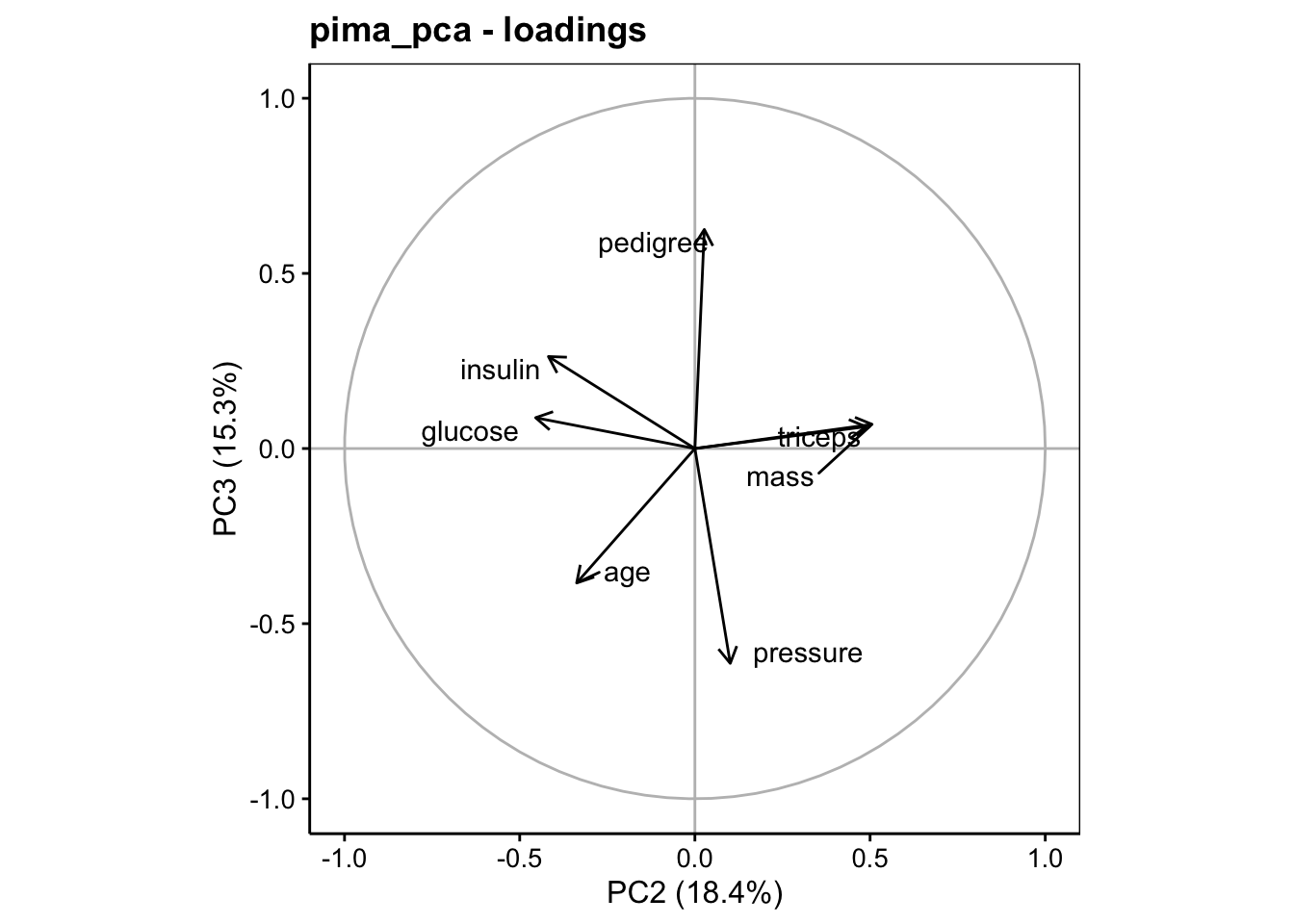
À vous de jouer !
La seconde représentation se fait dans l’espace des individus. Ici, nous allons projeter les points relatifs à chaque individu dans le plan de l’ACP choisi. Cela se réalise à l’aide de chart$scores() (l’aspect ratio est le rapport hauteur/largeur peut s’adapter) :
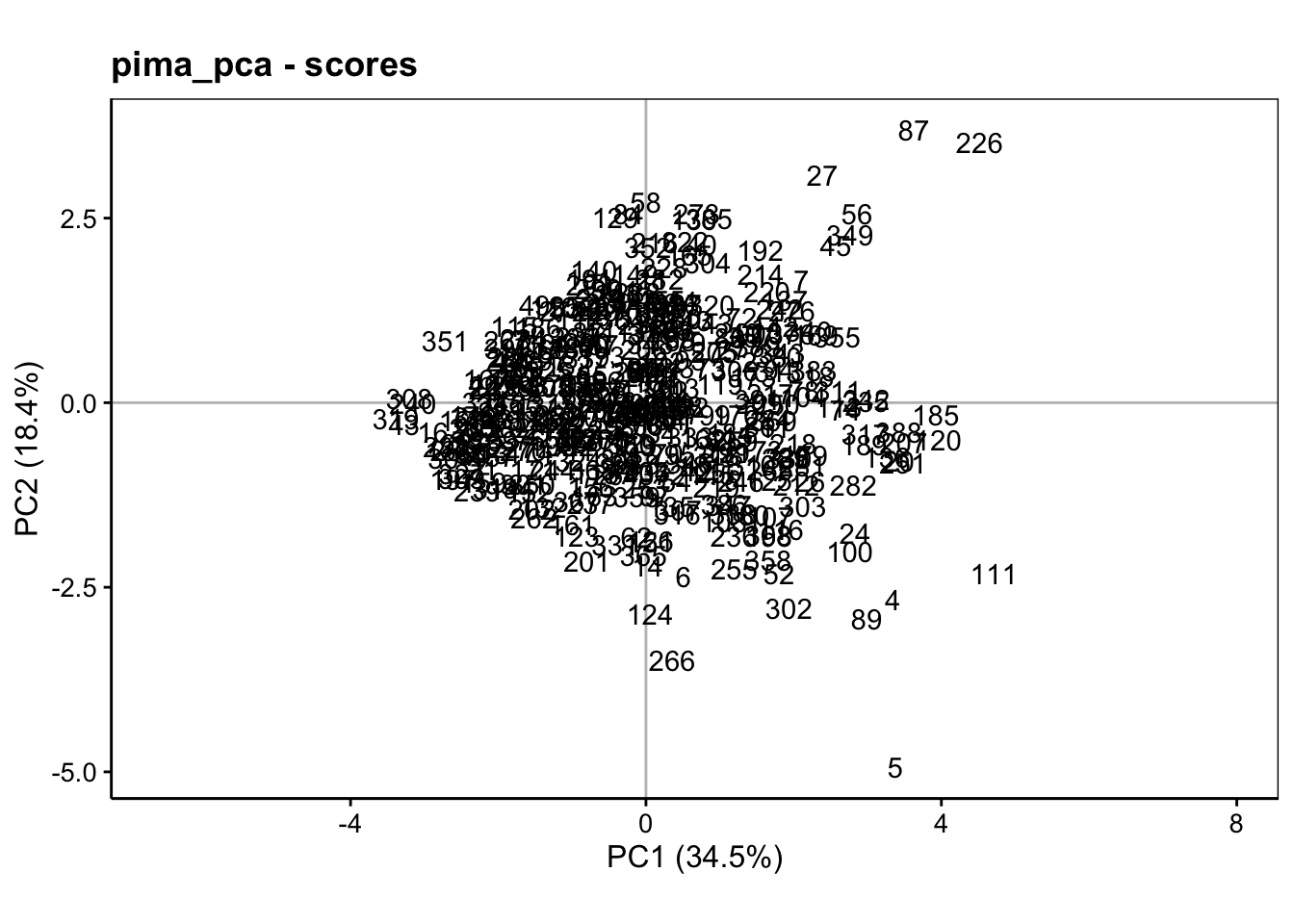
Ce graphique est peu lisible tel quel. Généralement, nous représentons d’autres informations utiles sous forme de labels et ou de couleurs différentes. Nous pouvons ainsi contraster les individus qui ont le diabète de ceux qui ne l’ont pas sur ce graphique et aussi ajouter des ellipses de confiance à 95% autour des deux groupes pour aider à la cerner à l’aide de stat_ellipse() :
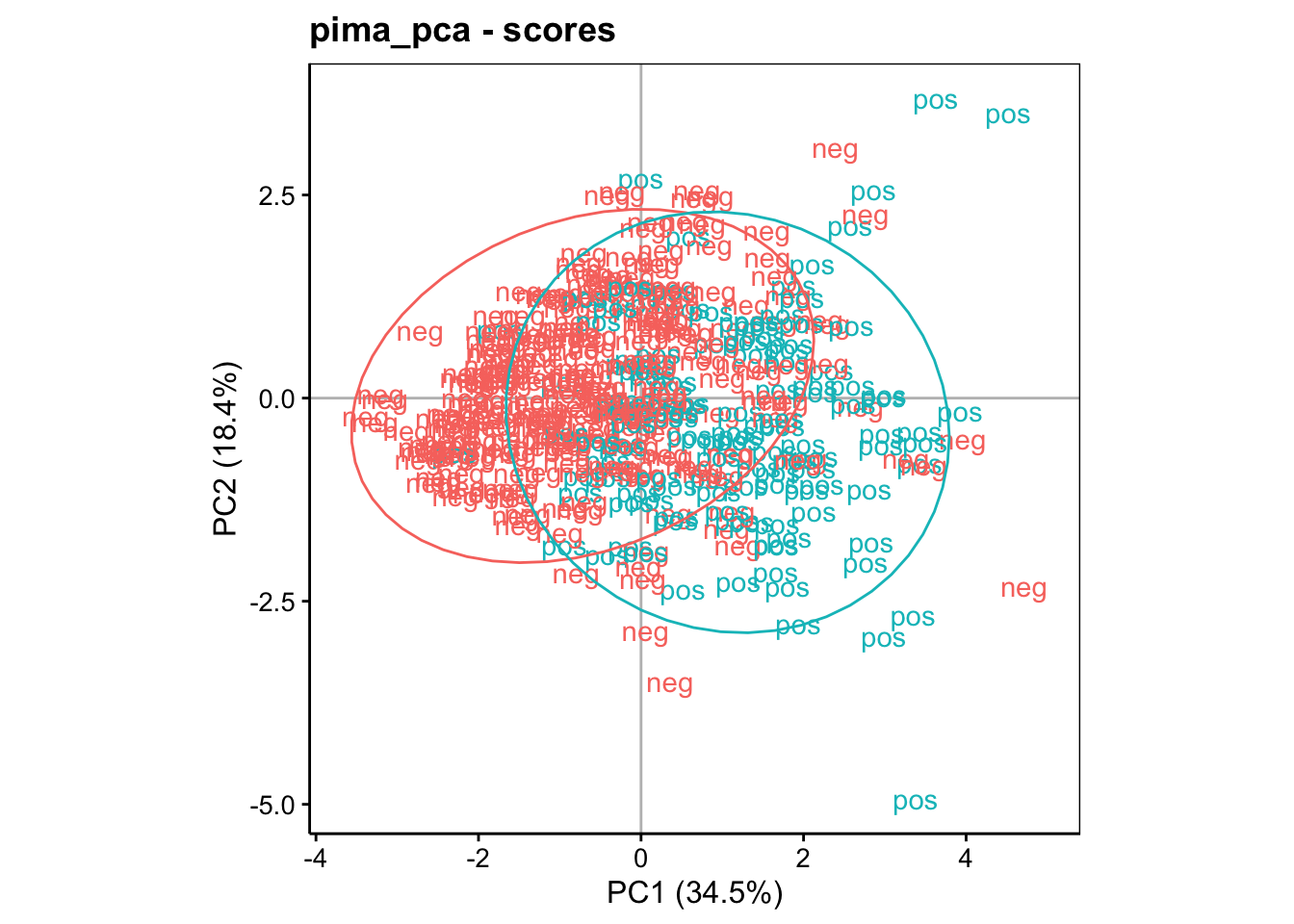
Ce graphique est nettement plus intéressant. Il s’interprète comme suit :
Nous savons que les individus plus âgés et ayant plus de glucose et d’insuline dans le sang sont dans le bas à droite du graphique. Or le groupe des diabétique, s’il ne se détache pas complètement tend à s’étaler plus dans cette région.
A l’inverse, le groupe des non diabétiques s’étale vers la gauche, c’est-à-dire dans une région reprenant les individus les plus jeunes et les moins gros.
Le graphique entre PC1 et PC3 (analyse du troisième axe) donne ceci :
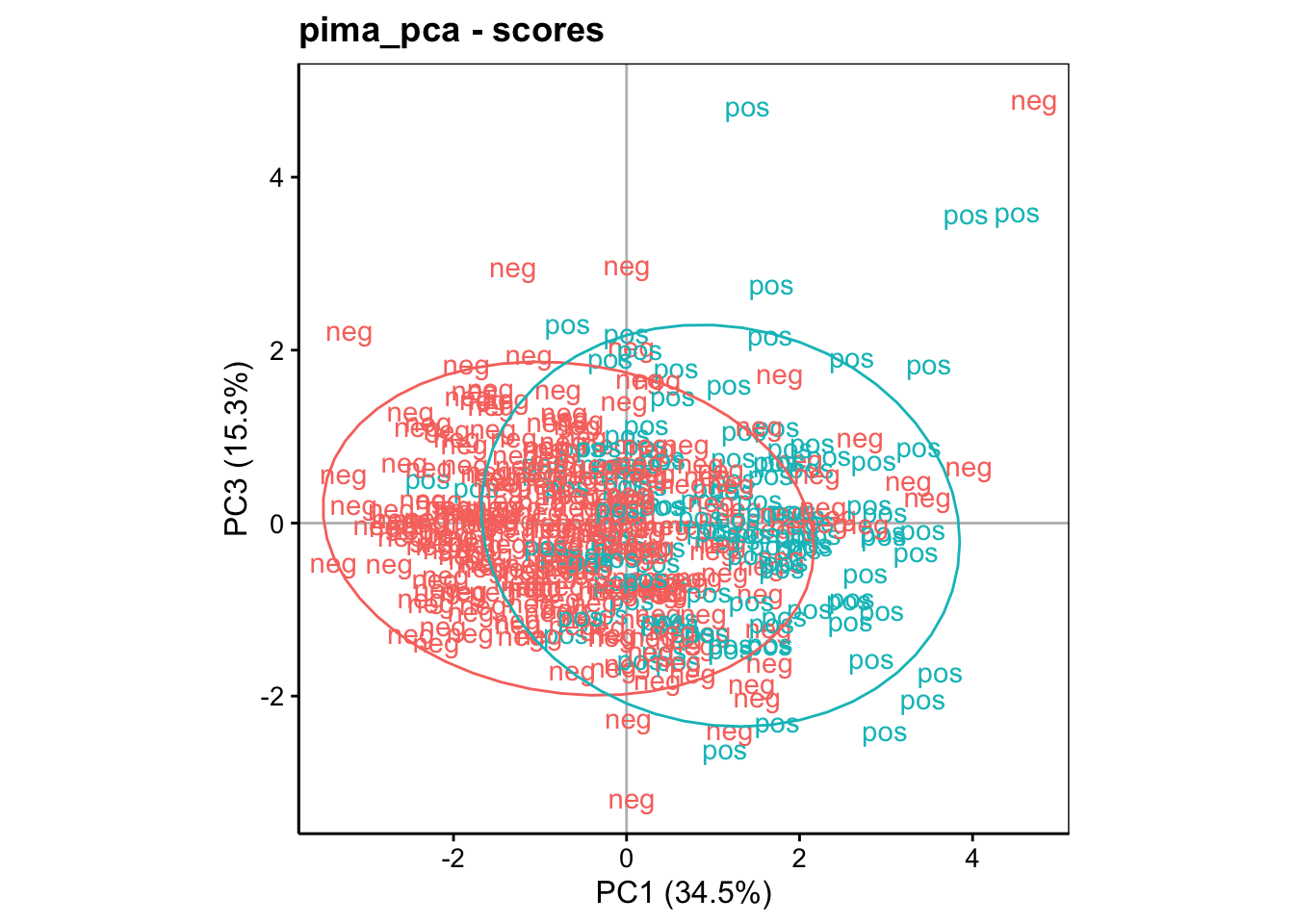
Ici, la séparation se fait essentiellement sur l’axe horizontal (PC1). Donc, les différentes de pedigree (élevé dans le haut du graphique) et de pression artérielle (élevée dans le bas du graphique) semblent être moins liés au diabète. Le graphique PC3 versus PC2 peut aussi être réalisé, mais il n’apporte rien de plus (et en pratique, nous l’éliminerions d’un rapport).
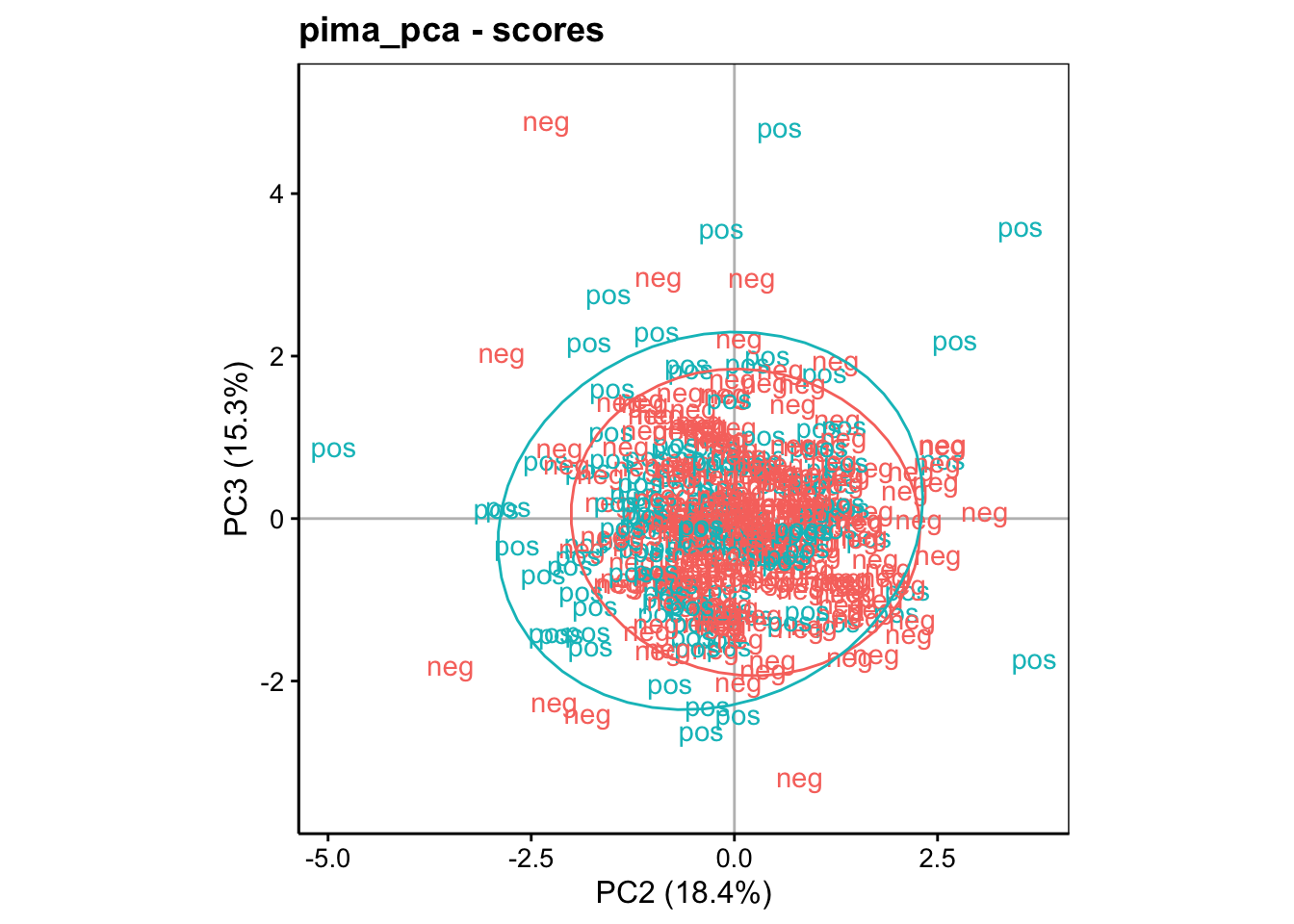
Étant donné que les deux graphiques (variables et individus) s’interprètent conjointement, nous pourrions être tentés de les superposer, cela s’appelle un biplot. Mais se pose alors un problème : celui de mettre à l’échelle les deux représentations pour qu’elles soient cohérentes entre elles. Ceci n’est pas facile et différentes représentations coexistent. L’argument scale = de la fonction chart$biplot() permet d’utiliser différentes mises à l’échelle. Enfin, ce type de graphique tend à être souvent bien trop encombré. Il est donc plus difficile à lire que les deux graphiques des variables et individus séparés. Voici ce que cela donne pour notre jeu de données exemple :
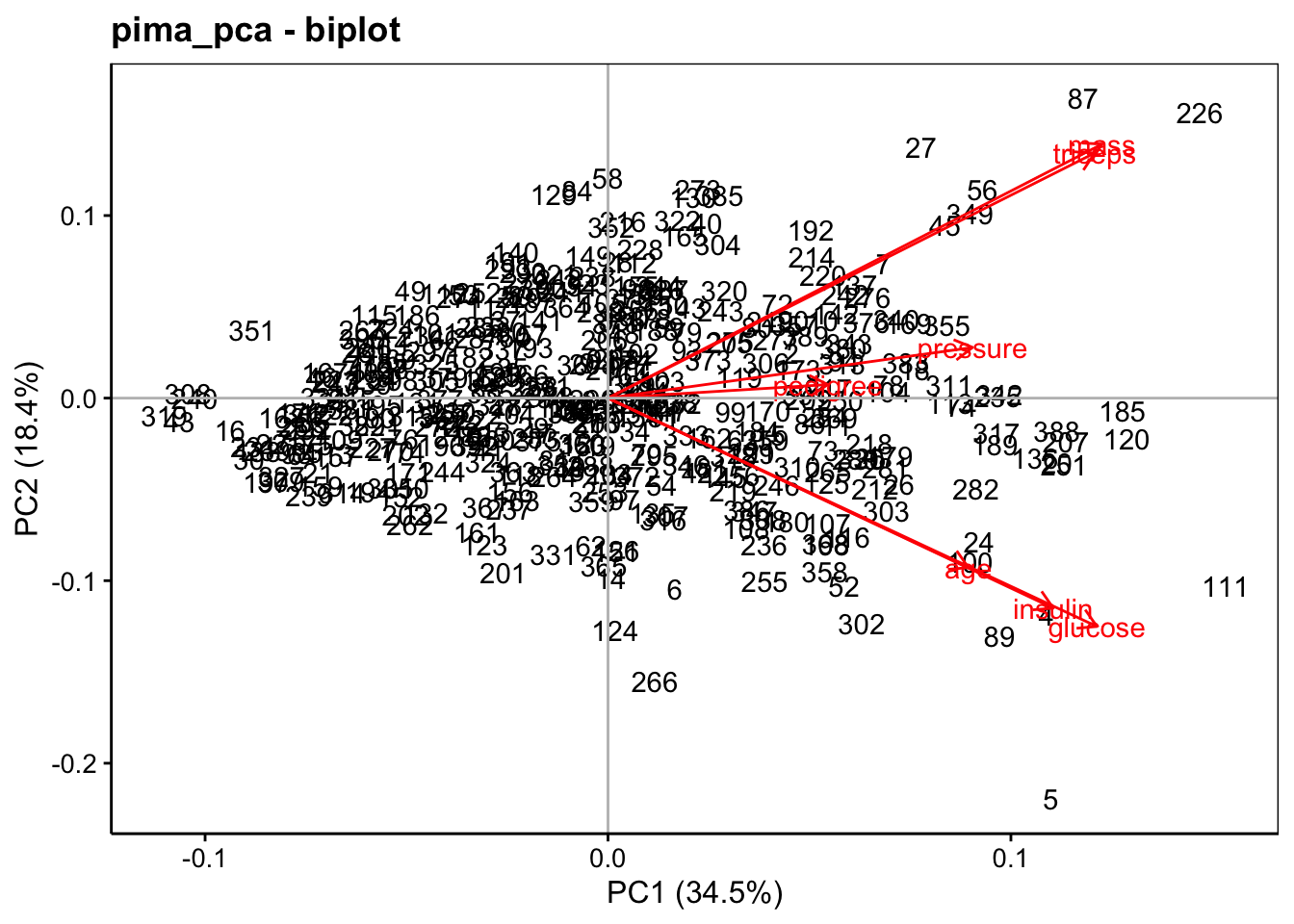
Bien moins lisible, en effet !
7.1.3 Biométrie d’oursin
Analysons à présent un autre jeu de données qui nous montrera l’importance de la transformation (linéarisation), du choix de réduire ou non (argument scale =), et l’effet d’un effet saturant, et comment s’en débarrasser. Il s’agit de la biométrie effectuée sur deux populations de l’oursin violet Paracentrotus lividus, une en élevage et une autre provenant du milieu naturel. Nous avons abondamment utilisé ce jeu de données en SDD I dans la section visualisation. Nous le connaissons bien, mais reprenons certains éléments essentiels ici…
# # A tibble: 421 x 19
# origin diameter1 diameter2 height buoyant_weight weight solid_parts
# <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# 1 Pêcherie 9.9 10.2 5 NA 0.522 0.478
# 2 Pêcherie 10.5 10.6 5.7 NA 0.642 0.589
# 3 Pêcherie 10.8 10.8 5.2 NA 0.734 0.677
# 4 Pêcherie 9.6 9.3 4.6 NA 0.370 0.344
# 5 Pêcherie 10.4 10.7 4.8 NA 0.610 0.559
# 6 Pêcherie 10.5 11.1 5 NA 0.610 0.551
# 7 Pêcherie 11 11 5.2 NA 0.672 0.605
# 8 Pêcherie 11.1 11.2 5.7 NA 0.703 0.628
# 9 Pêcherie 9.4 9.2 4.6 NA 0.413 0.375
# 10 Pêcherie 10.1 9.5 4.7 NA 0.449 0.398
# # … with 411 more rows, and 12 more variables: integuments <dbl>,
# # dry_integuments <dbl>, digestive_tract <dbl>, dry_digestive_tract <dbl>,
# # gonads <dbl>, dry_gonads <dbl>, skeleton <dbl>, lantern <dbl>, test <dbl>,
# # spines <dbl>, maturity <int>, sex <fct>Ici aussi nous avons des valeurs manquantes :
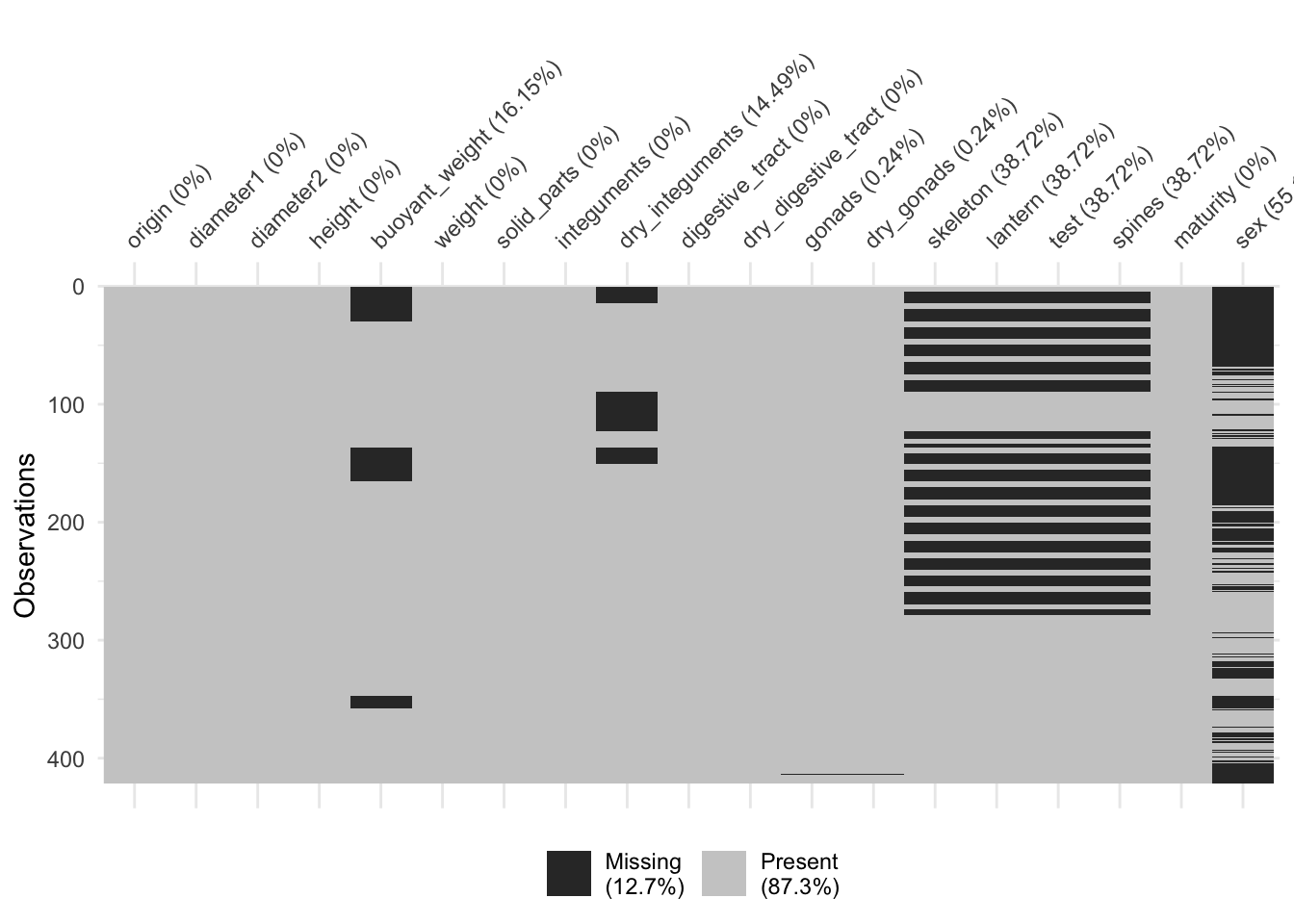
Ces valeurs manquantes sont rassemblées essentiellement dans les variables buoyant_weight, dry_integuments, les mesures relatives au squelette (skeleton, lantern, test et spines), et surtout au niveau de sex (impossible de déterminer le sexe des individus les plus jeunes). Si nous éliminons purement et simplement les lignes qui ont au moins une valeur manquante, nous perdons tous les individus jeunes, et c’est dommage. Nous allons donc d’abord éliminer les variables sex, ainsi que les quatre variables liées au squelette. Dans un second temps, nous appliquerons drop_na() sur ce qui reste :
# # A tibble: 319 x 14
# origin diameter1 diameter2 height buoyant_weight weight solid_parts
# <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# 1 Pêcherie 16.7 16.8 8.4 0.588 2.58 2.04
# 2 Pêcherie 19.9 20 9.2 1.10 4.26 3.66
# 3 Pêcherie 19.9 19.2 8.5 0.629 2.93 2.43
# 4 Pêcherie 19.3 19.8 10.2 0.781 3.71 3.09
# 5 Pêcherie 18.8 20 9.3 0.761 3.59 2.99
# 6 Pêcherie 21.5 20.9 9.6 1.13 4.98 4.42
# 7 Pêcherie 17.4 16.5 7.8 0.477 2.33 1.97
# 8 Pêcherie 21 21.2 10.8 1.23 5.4 4.55
# 9 Pêcherie 17.8 18.8 8.6 0.548 2.58 2.07
# 10 Pêcherie 19.7 19.6 9.7 0.862 3.59 3.08
# # … with 309 more rows, and 7 more variables: integuments <dbl>,
# # dry_integuments <dbl>, digestive_tract <dbl>, dry_digestive_tract <dbl>,
# # gonads <dbl>, dry_gonads <dbl>, maturity <int>Il nous reste 319 lignes des 421 initiales. Nous n’avons perdu qu’un quart des données, tout en nous privant seulement de quatre variables quantitatives liées au squelette (sexétant une variable qualitative, elle ne peut de toutes façons pas être introduite dans l’analyse, mais elle aurait pu servir pour colorer les individus).
| Name | urchin2 |
| Number of rows | 319 |
| Number of columns | 14 |
| _______________________ | |
| Column type frequency: | |
| factor | 1 |
| numeric | 13 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| origin | 0 | 1 | FALSE | 2 | Cul: 188, Pêc: 131 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| diameter1 | 0 | 1 | 32.78 | 11.71 | 14.60 | 23.25 | 31.50 | 39.65 | 65.60 | ▇▇▅▃▁ |
| diameter2 | 0 | 1 | 32.71 | 11.67 | 15.00 | 23.45 | 31.60 | 39.60 | 65.60 | ▇▇▆▃▁ |
| height | 0 | 1 | 16.78 | 6.25 | 7.30 | 11.10 | 16.20 | 21.50 | 32.20 | ▇▆▆▅▂ |
| buoyant_weight | 0 | 1 | 4.27 | 3.84 | 0.31 | 1.35 | 3.18 | 5.67 | 17.73 | ▇▃▁▁▁ |
| weight | 0 | 1 | 21.80 | 21.37 | 1.61 | 6.08 | 15.25 | 28.14 | 100.51 | ▇▂▁▁▁ |
| solid_parts | 0 | 1 | 16.52 | 15.27 | 1.46 | 4.96 | 11.73 | 21.69 | 73.14 | ▇▃▁▁▁ |
| integuments | 0 | 1 | 12.32 | 10.64 | 1.09 | 4.00 | 9.40 | 16.08 | 47.22 | ▇▃▂▁▁ |
| dry_integuments | 0 | 1 | 7.16 | 6.30 | 0.58 | 2.22 | 5.42 | 9.42 | 28.80 | ▇▃▂▁▁ |
| digestive_tract | 0 | 1 | 1.90 | 2.03 | 0.03 | 0.45 | 1.21 | 2.54 | 10.37 | ▇▂▁▁▁ |
| dry_digestive_tract | 0 | 1 | 0.23 | 0.21 | 0.01 | 0.07 | 0.17 | 0.31 | 1.02 | ▇▃▂▁▁ |
| gonads | 0 | 1 | 1.72 | 2.65 | 0.00 | 0.10 | 0.63 | 2.20 | 15.93 | ▇▁▁▁▁ |
| dry_gonads | 0 | 1 | 0.51 | 0.82 | 0.00 | 0.03 | 0.17 | 0.64 | 5.00 | ▇▁▁▁▁ |
| maturity | 0 | 1 | 0.37 | 0.71 | 0.00 | 0.00 | 0.00 | 0.00 | 2.00 | ▇▁▁▁▂ |
Nous avons 12 variables quantitatives continues. Notez la distribution très asymétrique et similaire (voir colonne hist) de toutes ces variables. les variables origin et maturity ne pourront pas être utilisées, mais seront éventuellement utiles pour colorer les points dans nos graphiques. Qu’en est-il des corrélations entre les 12 variables ?
| diameter1 | diameter2 | height | buoyant_weight | weight | solid_parts | integuments | dry_integuments | digestive_tract | dry_digestive_tract | gonads | dry_gonads | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| diameter1 | 1.00 | 1.00 | 0.98 | 0.95 | 0.96 | 0.96 | 0.97 | 0.96 | 0.91 | 0.93 | 0.80 | 0.79 |
| diameter2 | 1.00 | 1.00 | 0.97 | 0.95 | 0.96 | 0.96 | 0.97 | 0.96 | 0.91 | 0.93 | 0.80 | 0.79 |
| height | 0.98 | 0.97 | 1.00 | 0.93 | 0.92 | 0.93 | 0.94 | 0.93 | 0.88 | 0.91 | 0.76 | 0.75 |
| buoyant_weight | 0.95 | 0.95 | 0.93 | 1.00 | 0.99 | 0.99 | 0.99 | 1.00 | 0.92 | 0.94 | 0.88 | 0.87 |
| weight | 0.96 | 0.96 | 0.92 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.95 | 0.96 | 0.88 | 0.87 |
| solid_parts | 0.96 | 0.96 | 0.93 | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 0.95 | 0.95 | 0.91 | 0.90 |
| integuments | 0.97 | 0.97 | 0.94 | 0.99 | 0.99 | 0.99 | 1.00 | 1.00 | 0.93 | 0.95 | 0.87 | 0.85 |
| dry_integuments | 0.96 | 0.96 | 0.93 | 1.00 | 0.99 | 0.99 | 1.00 | 1.00 | 0.92 | 0.94 | 0.87 | 0.86 |
| digestive_tract | 0.91 | 0.91 | 0.88 | 0.92 | 0.95 | 0.95 | 0.93 | 0.92 | 1.00 | 0.98 | 0.81 | 0.81 |
| dry_digestive_tract | 0.93 | 0.93 | 0.91 | 0.94 | 0.96 | 0.95 | 0.95 | 0.94 | 0.98 | 1.00 | 0.82 | 0.82 |
| gonads | 0.80 | 0.80 | 0.76 | 0.88 | 0.88 | 0.91 | 0.87 | 0.87 | 0.81 | 0.82 | 1.00 | 0.99 |
| dry_gonads | 0.79 | 0.79 | 0.75 | 0.87 | 0.87 | 0.90 | 0.85 | 0.86 | 0.81 | 0.82 | 0.99 | 1.00 |

Toutes les corrélations sont positives, et certaines sont très élevées. Cela indique que plusieurs variables sont (pratiquement complètement) redondantes, par exemple, diameter1 et diameter2. Un effet principal semble dominer.
Si nous refaisons quelques graphiques, nous nous rappelons que les relations ne sont pas linéaires, par exemple, entre diameter1 et weight :
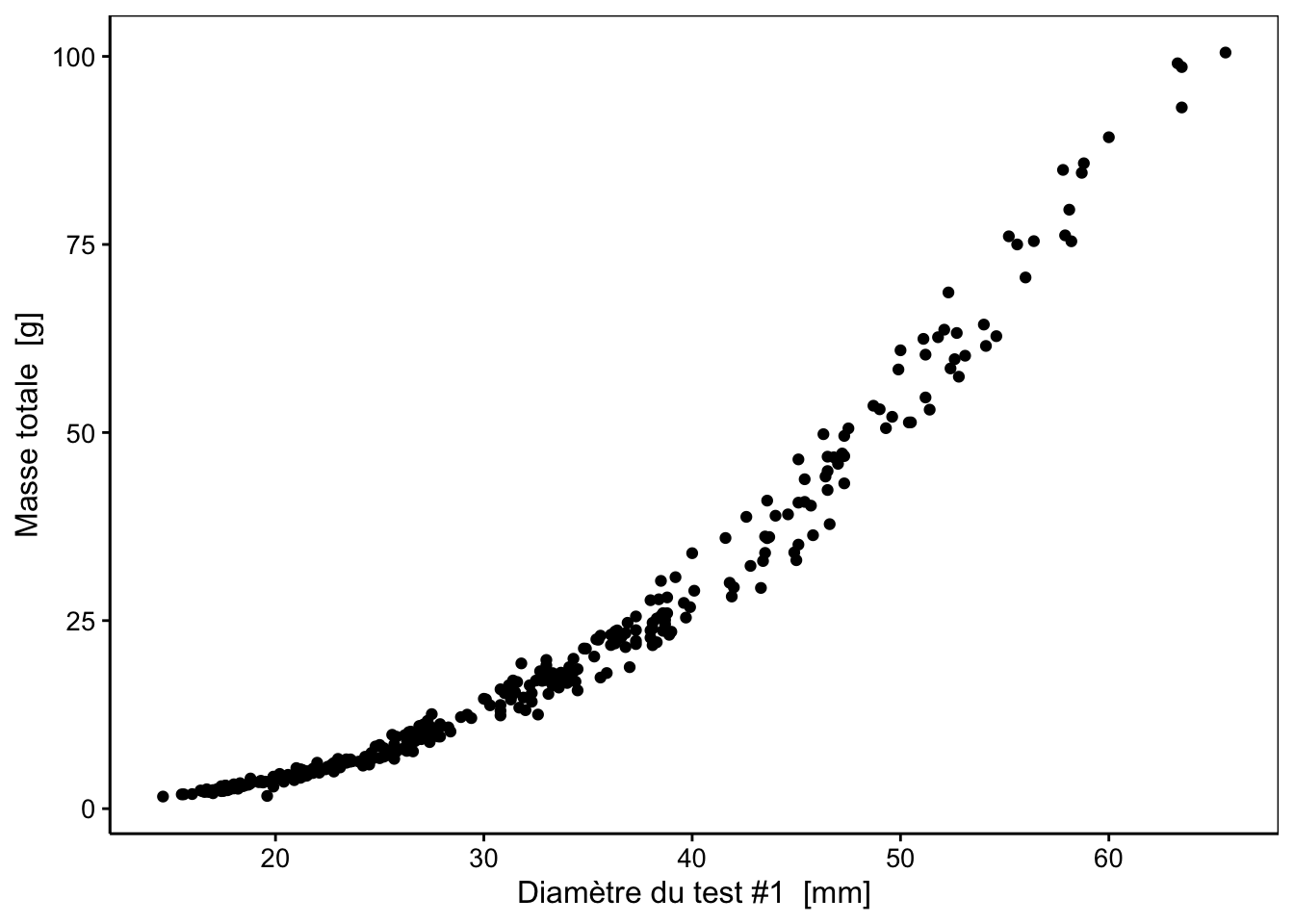
Ce type de relation, dite allométrique se linéarise très bien en effectuant une transformation double-logarithme, comme nous pouvons le constater sur le graphique suivant :
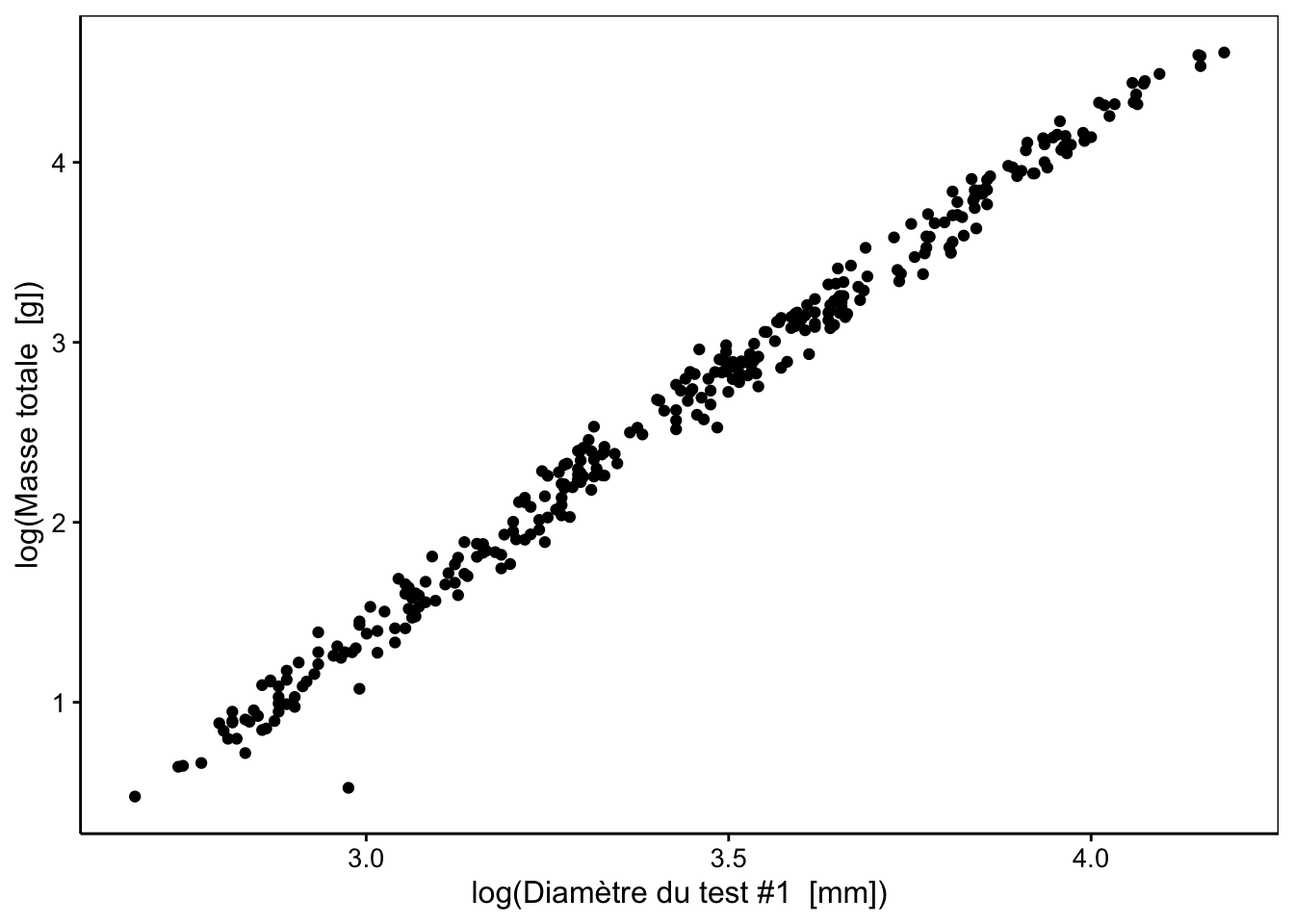
Attention toutefois à la transformation logarithmique appliquée sur des données qui peuvent contenir des zéros (par exemple, gonads ou dry_gonads). Dans ce cas, la transformation logarithme(x + 1) réalisée avec la fonction log1p() est plus indiquée. Nous allons ici transformer toutes les variables en log(x + 1). C’est assez fastidieux à faire avec mutate(), mais nous pouvons l’utiliser directement sur le tableau entier réduit aux variables quantitatives continues seules lors de l’appel à pca() comme suit :
urchin2 %>.%
select(., -origin, -maturity) %>.% # Élimine les variables non quantitatives
log1p(.) %>.% # Transforme toutes les autres en log(x + 1)
pca(., scale = TRUE) -> urchin2_pca # Effectue l'ACP après standardisationNous avons standardisé les données puisqu’elles sont mesurées dans des unités différentes (longueurs en mm, masses en g). Voici ce que donne notre ACP :
# Importance of components (eigenvalues):
# PC1 PC2 PC3 PC4 PC5 PC6 PC7
# Variance 11.219 0.5010 0.1813 0.03862 0.02601 0.01657 0.00931
# Proportion of Variance 0.935 0.0418 0.0151 0.00322 0.00217 0.00138 0.00078
# Cumulative Proportion 0.935 0.9767 0.9918 0.99503 0.99720 0.99858 0.99936
# PC8 PC9 PC10 PC11 PC12
# Variance 0.00336 0.00210 0.00108 0.00082 0.00034
# Proportion of Variance 0.00028 0.00017 0.00009 0.00007 0.00003
# Cumulative Proportion 0.99964 0.99981 0.99990 0.99997 1.00000
#
# Loadings (eigenvectors, rotation matrix):
# PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8
# diameter1 0.295 -0.162 -0.441 0.237 -0.174 0.177 0.242
# diameter2 0.295 -0.166 -0.449 0.249 -0.178 0.157 0.124
# height 0.291 -0.218 0.154 -0.106 -0.902
# buoyant_weight 0.296 0.120 0.509 0.124 0.530
# weight 0.296 -0.149 -0.145
# solid_parts 0.297 -0.106 0.127 0.234 -0.594
# integuments 0.296 -0.159 0.157 0.153 0.125 -0.396
# dry_integuments 0.296 -0.115 0.160 0.455 0.114 0.105
# digestive_tract 0.288 -0.571 -0.187 0.485 -0.519 0.201
# dry_digestive_tract 0.283 -0.702 0.217 -0.278 0.513 -0.161
# gonads 0.271 0.568 0.226 0.575 0.430 0.143
# dry_gonads 0.259 0.697 -0.104 -0.465 -0.453 -0.111
# PC9 PC10 PC11 PC12
# diameter1 -0.706
# diameter2 0.688 0.263
# height
# buoyant_weight 0.265 -0.504
# weight 0.116 -0.912
# solid_parts 0.216 0.638
# integuments 0.148 -0.702 -0.371
# dry_integuments 0.128 -0.133 0.774
# digestive_tract
# dry_digestive_tract
# gonads
# dry_gonadsWhaaa ! Plus de 93% de la variance représentée sur le premier axe. Ça parait parfait ! Voici le graphique des éboulis :
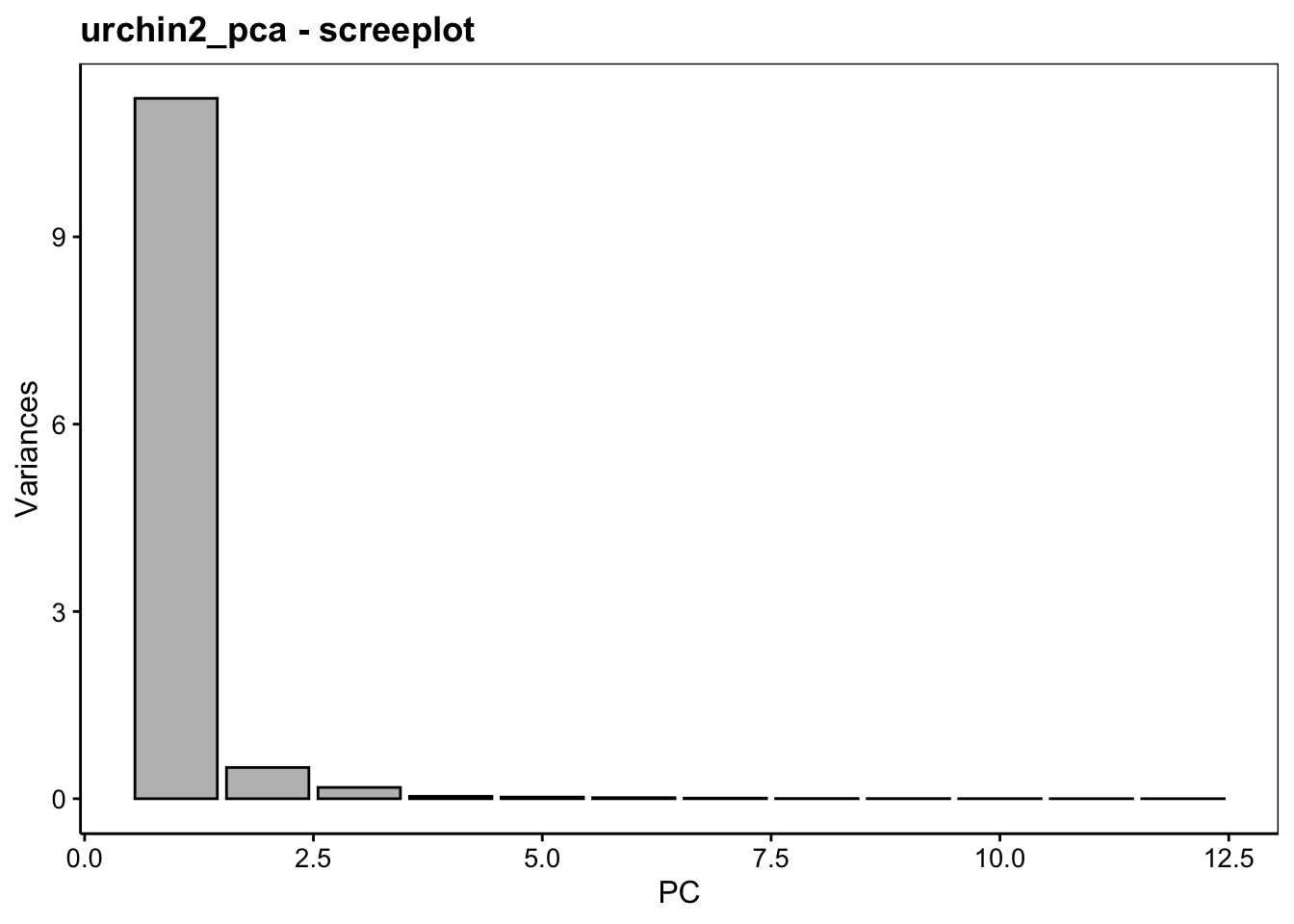
Ne vous réjouissez pas trop vite. Nous avons ici un effet saturant lié au fait que toutes les variables sont positivement corrélées entre elles. Cet effet est évident. Ici, c’est la taille. Nous allons conclure que plus un oursin est gros, plus ses dimensions et ses masses sont importante. C’est trivial et d’un intérêt très limité, avouons-le.
Notez aussi les valeurs relativement faibles, mais homogènes de toutes les variables sur l’axe PC1 dans le tableau des vecteurs propres, avec des valeurs comprises entre 0,26 et 0,30. Le graphique des variables est également très moche dans le premier plan de l’ACP, même si un effet différent relatif aux gonades apparaît tout de même sur l’axe PC2, il ne compte que pour 4,2% de la variance totale :
# Warning: ggrepel: 8 unlabeled data points (too many overlaps). Consider
# increasing max.overlaps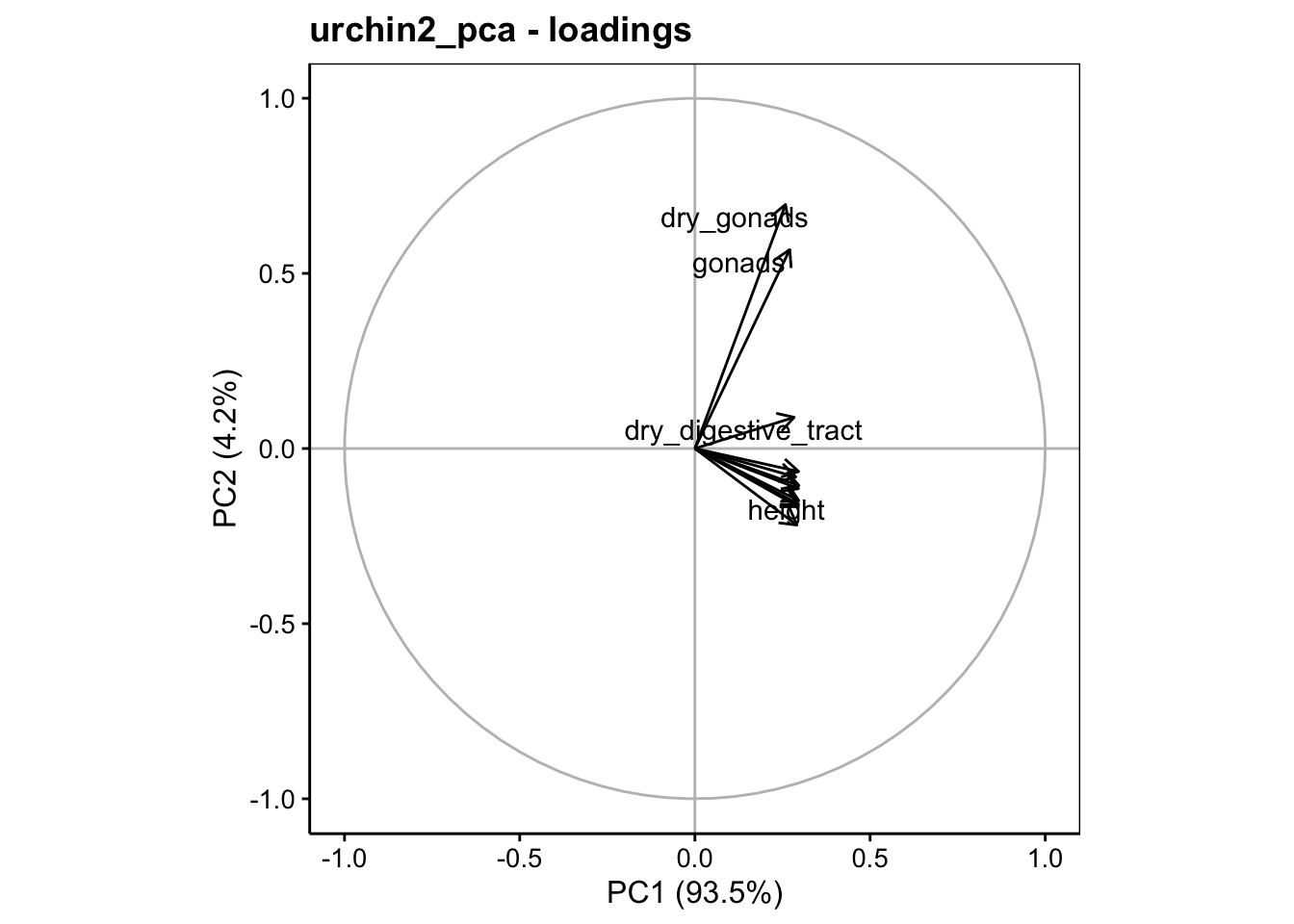
Recommençons tout de suite l’analyse en éliminant l’effet saturant. Nous pourrons considérer comme référence de la taille, par exemple, la masse immergée (buoyant weight) connue comme étant une mesure pouvant être mesurée très précisément. Elle fait partie des variables les mieux corrélées sur l’axe PC1, représentant ainsi très bien cet effet saturant que nous voulons éliminer. Voici notre calcul :
urchin2 %>.%
select(., -origin, -maturity, -buoyant_weight) %>.% # Élimination des variables inutiles
(. / urchin2$buoyant_weight) %>.% # Division par buoyant_weight
log1p(.) -> urchin3 # Transformation log(x + 1)
head(urchin3)# diameter1 diameter2 height weight solid_parts integuments dry_integuments
# 1 3.380877 3.386644 2.726760 1.683990 1.497119 1.388714 1.030481
# 2 2.953357 2.958109 2.240741 1.587131 1.468302 1.345385 1.022630
# 3 3.485925 3.451231 2.675524 1.733496 1.582091 1.478861 1.051165
# 4 3.247200 3.271795 2.643585 1.749467 1.600897 1.441601 1.049797
# 5 3.247291 3.306831 2.582396 1.744070 1.595668 1.424509 1.048737
# 6 3.000850 2.973973 2.254397 1.690963 1.594759 1.406850 1.034084
# digestive_tract dry_digestive_tract gonads dry_gonads
# 1 0.1039141 0.02667720 0.009140213 0.001529182
# 2 0.1806157 0.04368131 0.040178983 0.007821777
# 3 0.1683868 0.03608357 0.000000000 0.000000000
# 4 0.2061975 0.04764294 0.023167059 0.002174887
# 5 0.3154008 0.06613980 0.028901124 0.004984271
# 6 0.3464496 0.05538973 0.016565715 0.003104904Refaisons notre ACP sur urchin3 ainsi calculé :
# Importance of components (eigenvalues):
# PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8
# Variance 4.687 3.353 1.273 0.9666 0.3668 0.1724 0.10547 0.04761
# Proportion of Variance 0.426 0.305 0.116 0.0879 0.0333 0.0157 0.00959 0.00433
# Cumulative Proportion 0.426 0.731 0.847 0.9345 0.9678 0.9835 0.99308 0.99741
# PC9 PC10 PC11
# Variance 0.01943 0.00834 0.00068
# Proportion of Variance 0.00177 0.00076 0.00006
# Cumulative Proportion 0.99918 0.99994 1.00000
#
# Loadings (eigenvectors, rotation matrix):
# PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8
# diameter1 -0.425 0.145 -0.297 -0.101 0.101
# diameter2 -0.425 -0.101 0.143 -0.296 -0.103
# height -0.427 0.131 -0.300 0.141
# weight 0.189 -0.428 0.216 0.497 -0.672 -0.145
# solid_parts -0.495 0.254 -0.117 0.335 -0.245 -0.662
# integuments -0.142 -0.463 0.152 0.283 0.165 0.345 0.667 0.266
# dry_integuments -0.259 -0.242 0.173 0.533 -0.669 -0.161 -0.277
# digestive_tract 0.214 -0.370 -0.448 -0.102 0.388 -0.462 0.468
# dry_digestive_tract -0.360 -0.485 -0.401 -0.429 -0.338 0.382 -0.155
# gonads 0.374 0.438 -0.257 -0.223
# dry_gonads 0.371 0.440 -0.269 -0.162 -0.122 0.446
# PC9 PC10 PC11
# diameter1 0.400 0.714
# diameter2 0.425 -0.700
# height 0.197 -0.790
# weight 0.109
# solid_parts -0.223
# integuments
# dry_integuments
# digestive_tract 0.148
# dry_digestive_tract
# gonads 0.725 0.130
# dry_gonads -0.589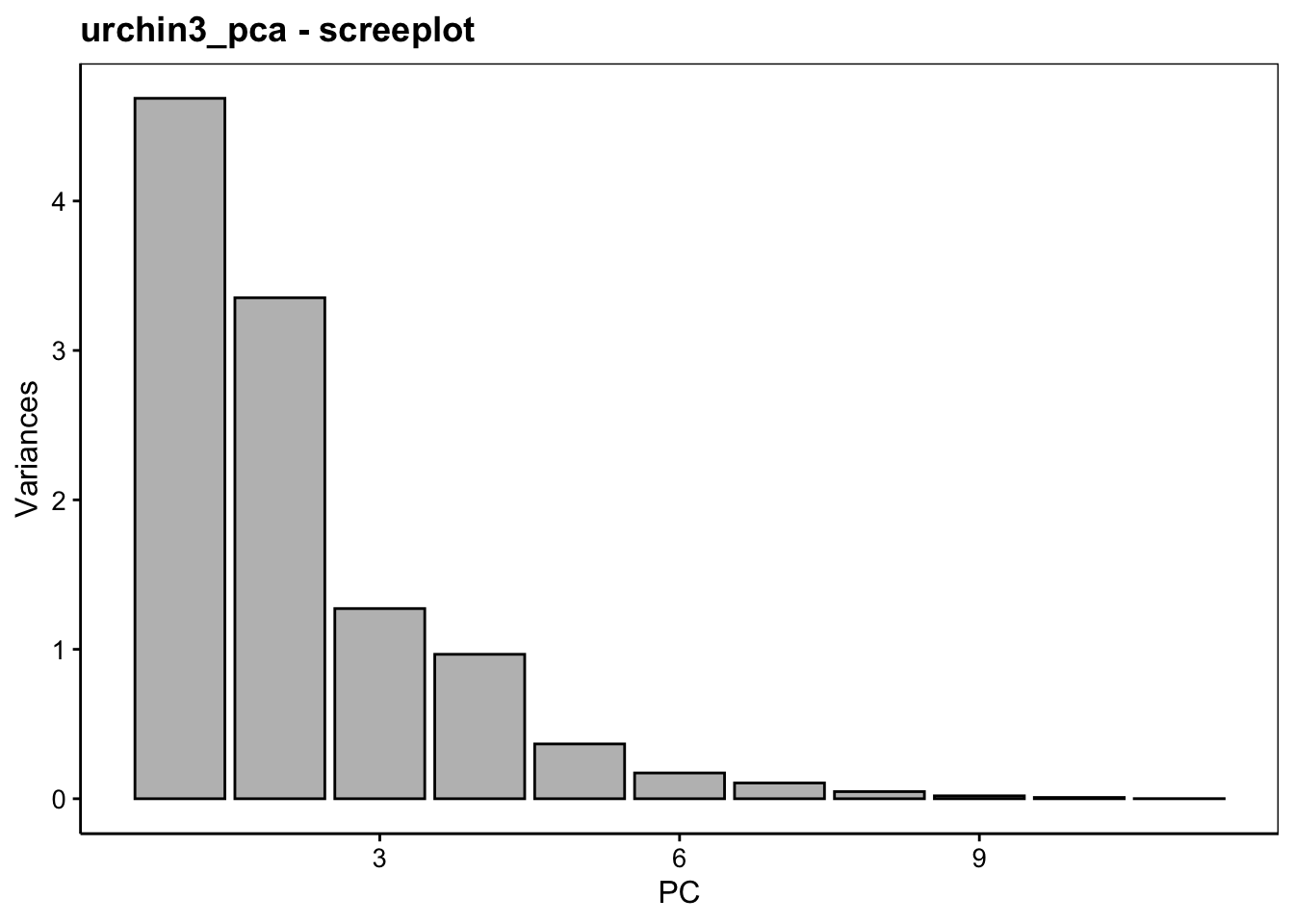
Maintenant que l’effet saturant est éliminé, la répartition des variances sur les axes se fait mieux. L’axe PC1 contraste les diamètres avec les gonades, l’axe PC2 représente les masses somatiques (dans l’ordre inverse), et l’axe PC3 contraste de manière intéressante les masses du tube digestif avec celles des gonades (le tout en ratios sur la masse immergée, ne l’oublions pas). Les deux premiers axes reprennent 73% de la variance, mais il semble qu’un effet intéressant se marque également sur PC3 avec 85% de la variance totale sur les trois premiers axes.
Tout ceci est également visible sur les graphiques dans l’espace des variables (plans PC1 - PC2 et PC2 - PC3 représentés ici).
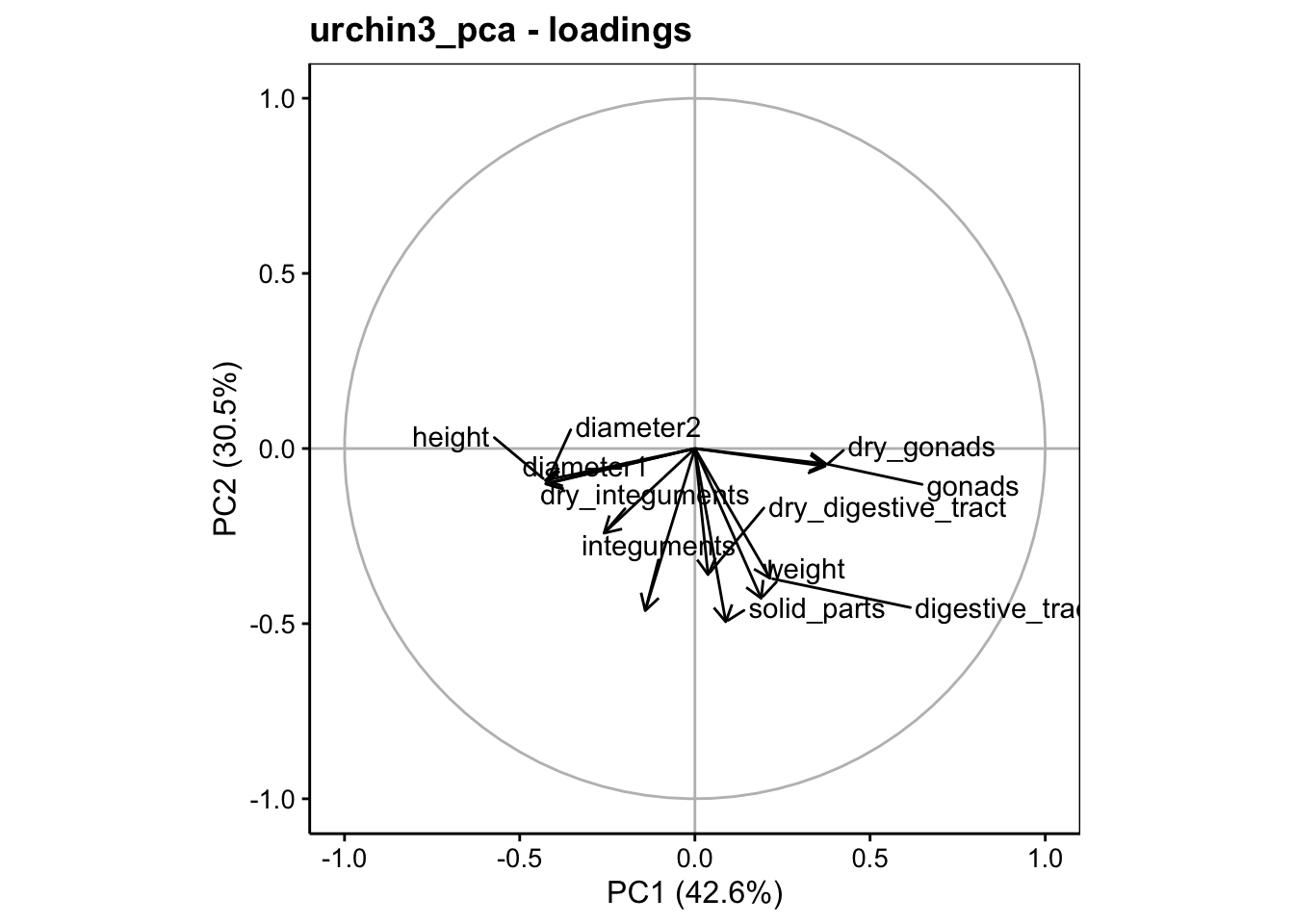
# Warning: ggrepel: 1 unlabeled data points (too many overlaps). Consider
# increasing max.overlaps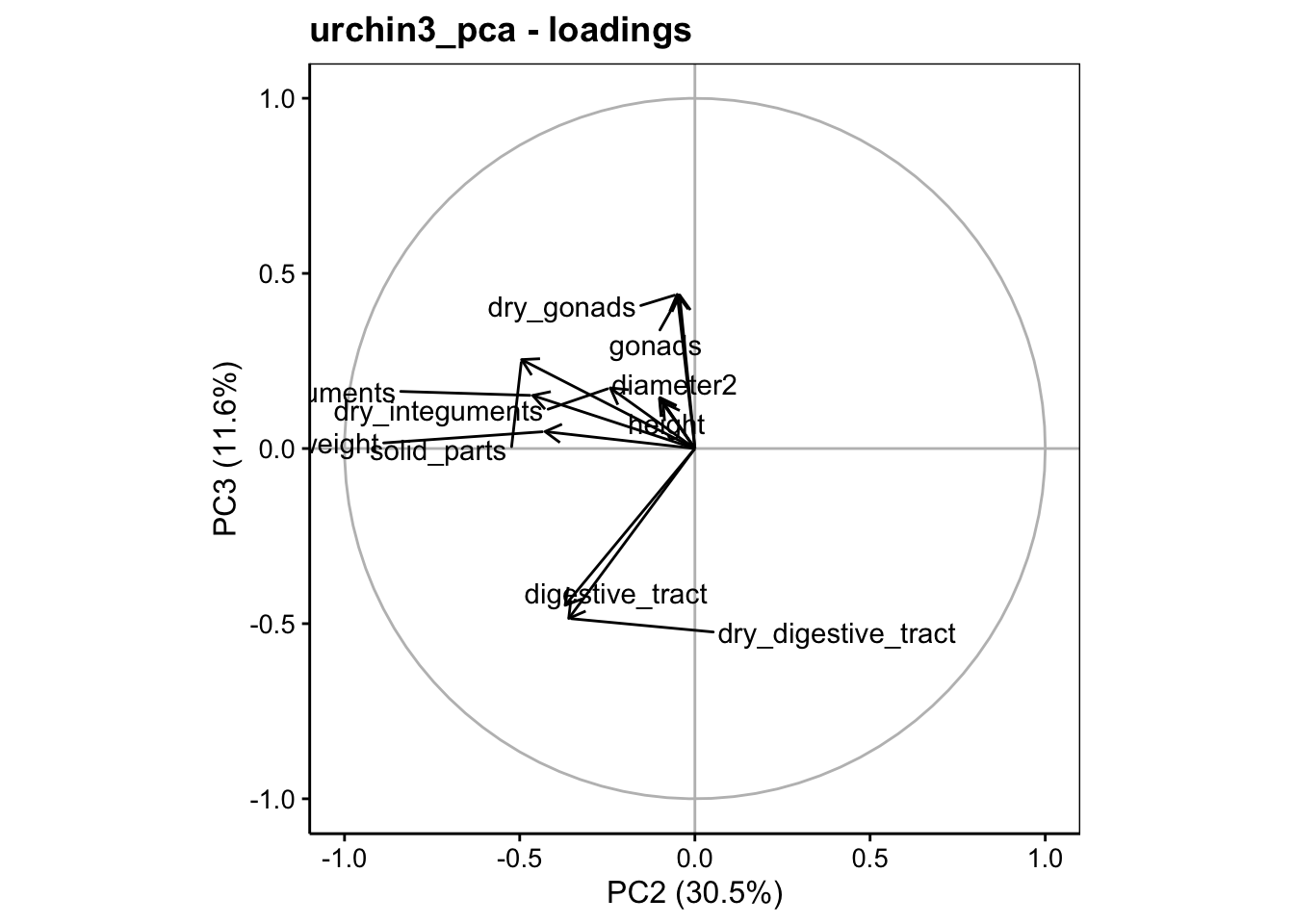
Enfin, dans l’espace des individus, avec l’origine reprise en couleur, nous observons ceci dans le premier plan de l’ACP :
chart$scores(urchin3_pca, choices = c(1, 2),
col = urchin2$origin, labels = urchin2$maturity, aspect.ratio = 3/5) +
theme(legend.position = "right") +
stat_ellipse()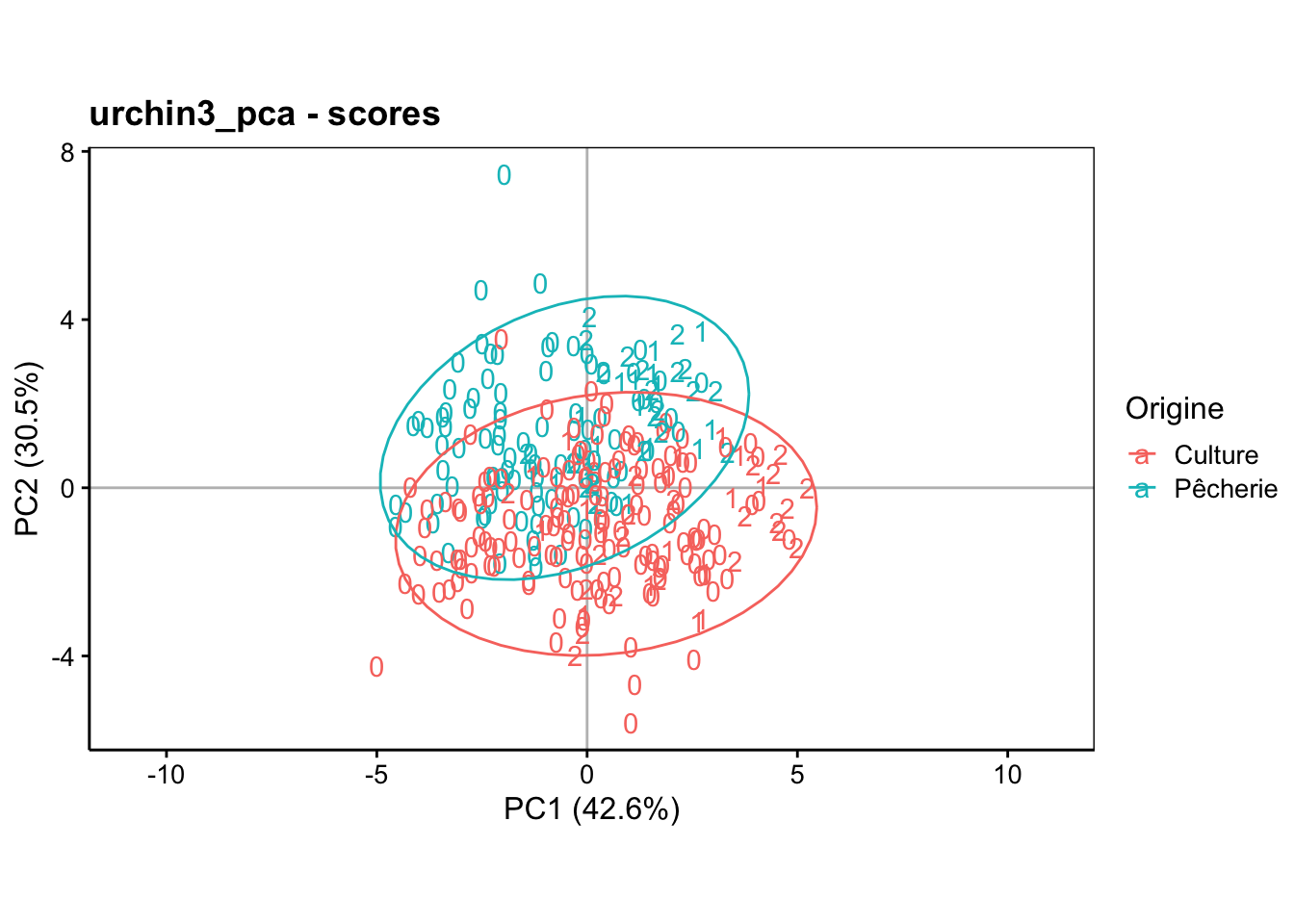
Et pour le plan PC2 - PC3 :
chart$scores(urchin3_pca, choices = c(2, 3),
col = urchin2$origin, labels = urchin2$maturity, aspect.ratio = 3/5) +
theme(legend.position = "right") +
stat_ellipse()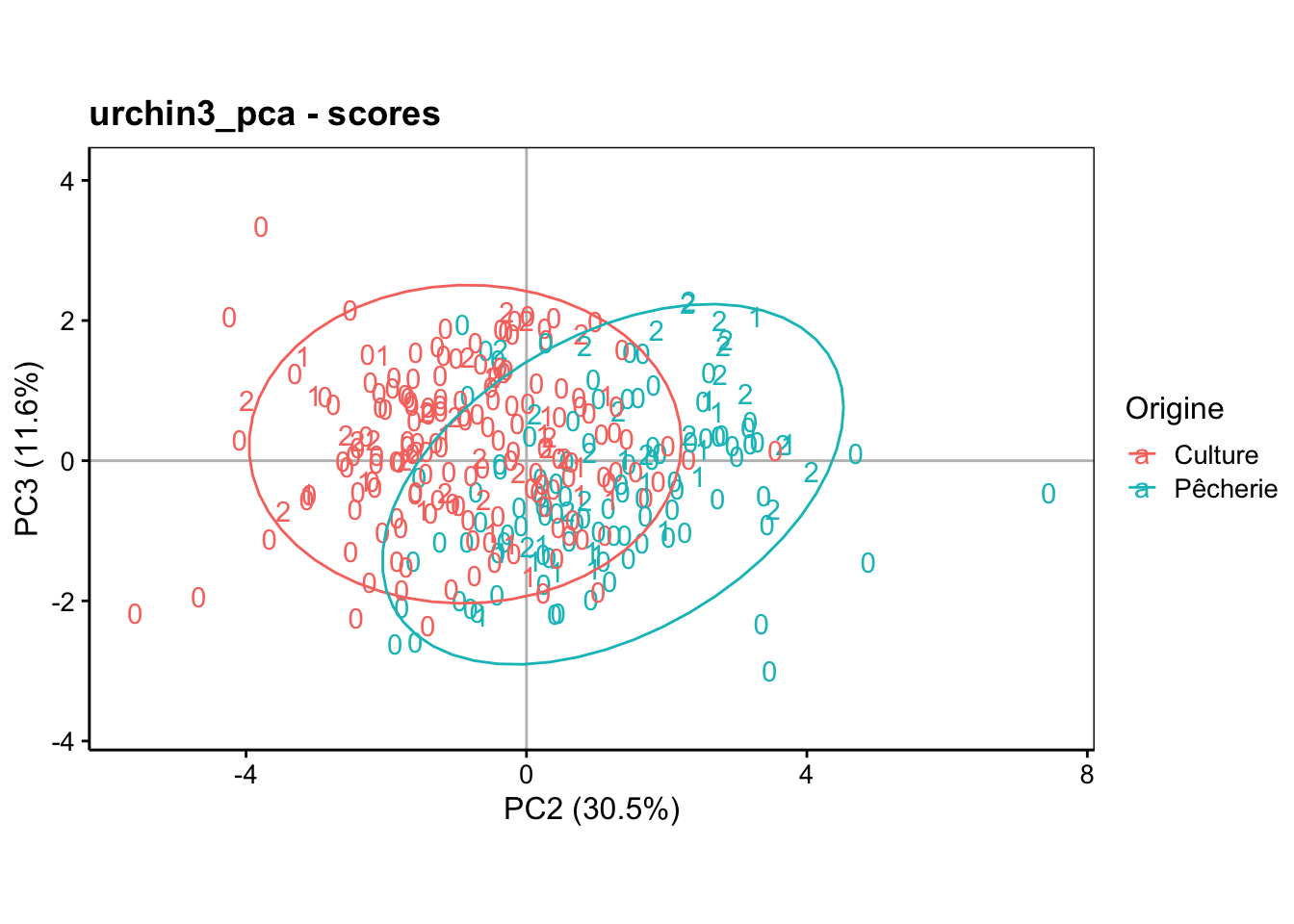
Vous devriez pouvoir interpréter ces résultats par vous-même maintenant.
7.1.4 Visualisation de données quantitatives
7.1.4.1 Deux dimensions
Le nuage de points est le graphe idéal pour visualiser la distribution des données bivariées pour deux variables quantitatives. Il permet de visualiser également une association entre deux variables. Il permet aussi de visualiser comment deux ou plusieurs groupes peuvent être séparés en fonction de ces deux variables.
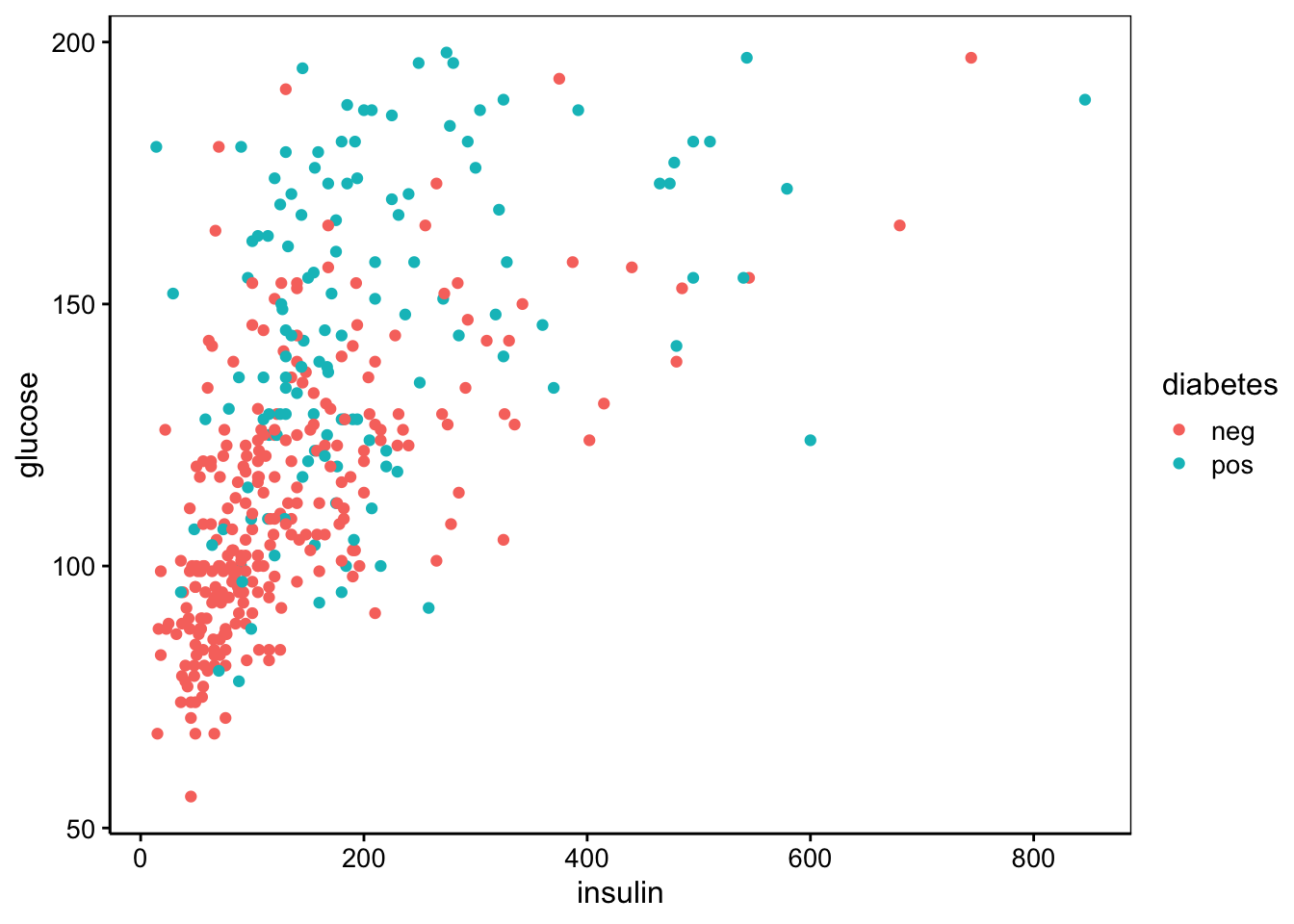
7.1.4.2 Trois dimensions
Le nuage de points en pseudo-3D est l’équivalent pour visualiser trois variables quantitatives simultanément. Il est nécessaire de rendre l’effet de la troisième dimension (perspective, variation de taille des objets, …). La possibilité de faire tourner l’objet 3D virtuel est indispensable pour concrétiser l’effet 3D et pour le visionner sous différents angles
Le package {rgl} permet de réaliser ce genre de graphique 3D interactif (que vous pouvez faire tourner dans l’orientation que vous voulez à la souris). Dans un document R Markdown, il faut absolument configurer {knitr} qui est responsable de l’inclusion des graphiques R dans le document comme ceci avant toute chose :
Ensuite, nous pouvons réaliser le graphique 3D {rgl} :
Enfin, nous l’introduisons dans le document à l’aide de ceci :
À noter que cela ne fonctionne que pour les documents au format HTML.
7.1.4.3 Plus de trois dimensions
Déjà à trois dimensions la visualisation devient délicate, mais au delà, cela devient pratiquement mission impossible. La matrice de nuages de points peut rendre service ici, mais dans certaines limites (tous les angles de vue ne sont pas accessibles).
# Registered S3 method overwritten by 'GGally':
# method from
# +.gg ggplot2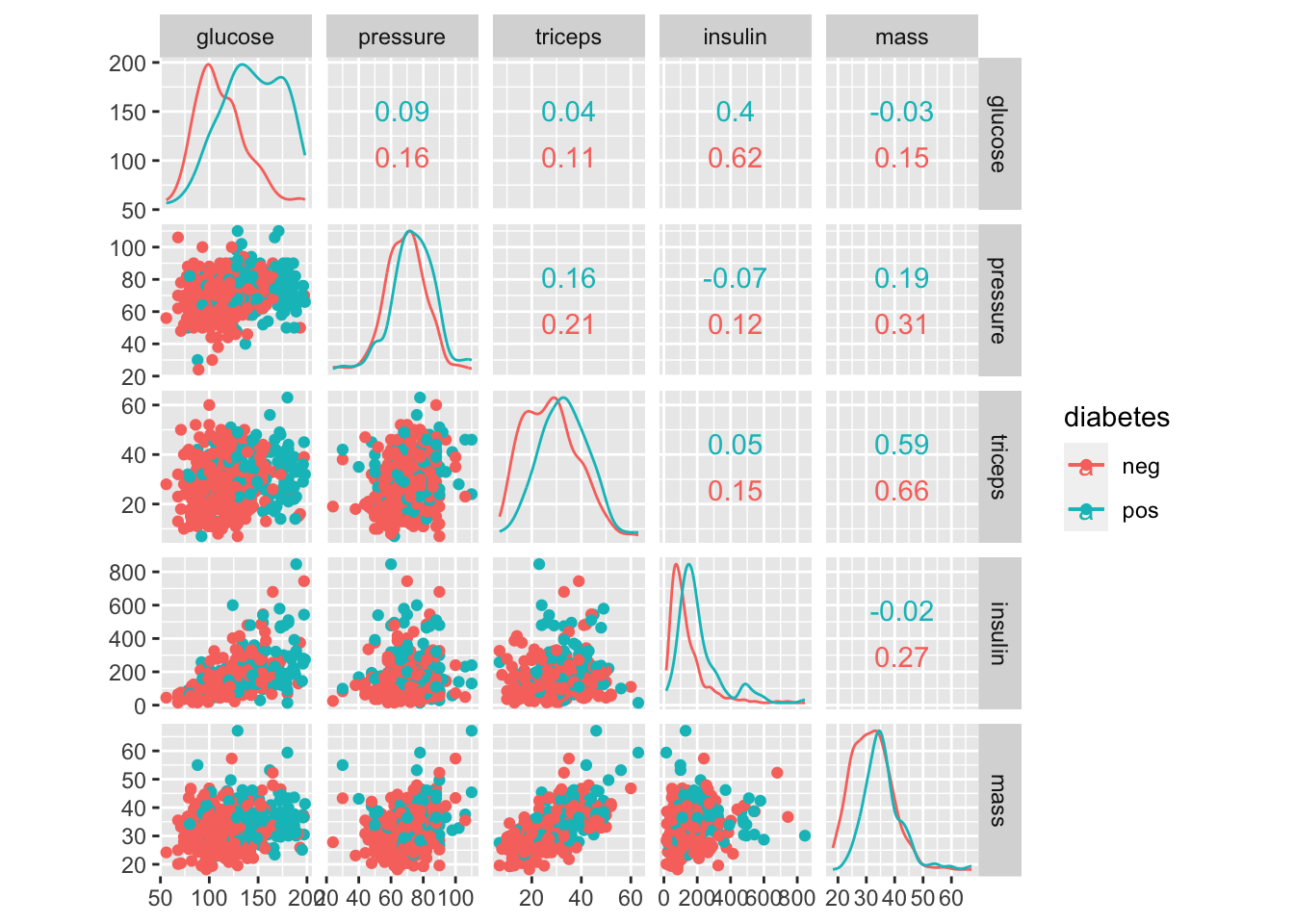
Nous voyons qu’ici nous atteignons les limites des possibilités. C’est pour cela que, pour des données multivariées comportant beaucoup de variables quantitatives, les techniques de réduction des dimensions comme l’ACP sont indispensables.
7.1.5 ACP : mécanisme
Nous allons partir d’un exemple presque trivial pour illustrer le principe de l’ACP. Comment réduire un tableau bivarié en une représentation des individus en une seule dimension (classement sur une droite) avec perte minimale d’information ? Par exemple, en partant de ces données fictives :
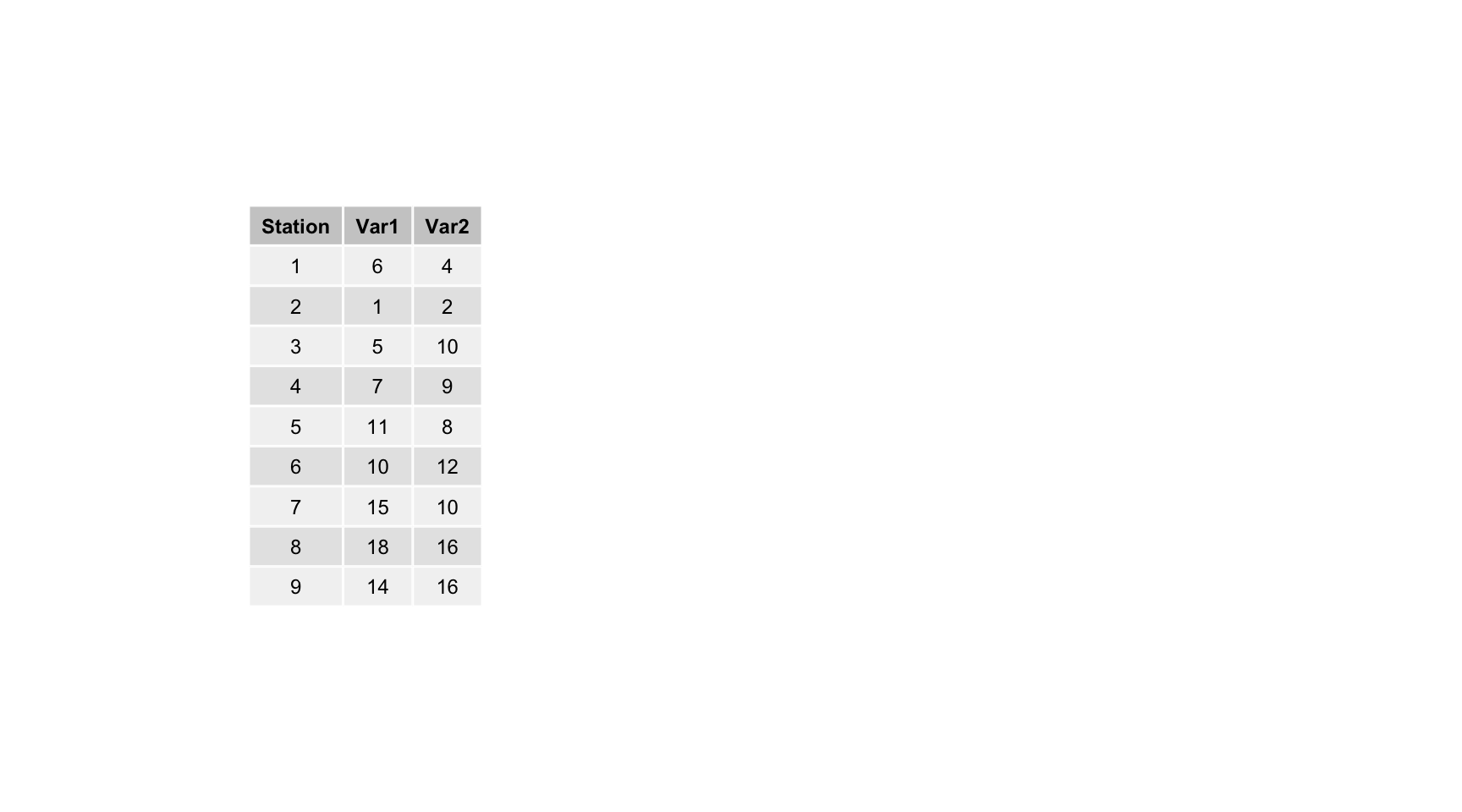
Voici une représentation graphique 2D de ces données :
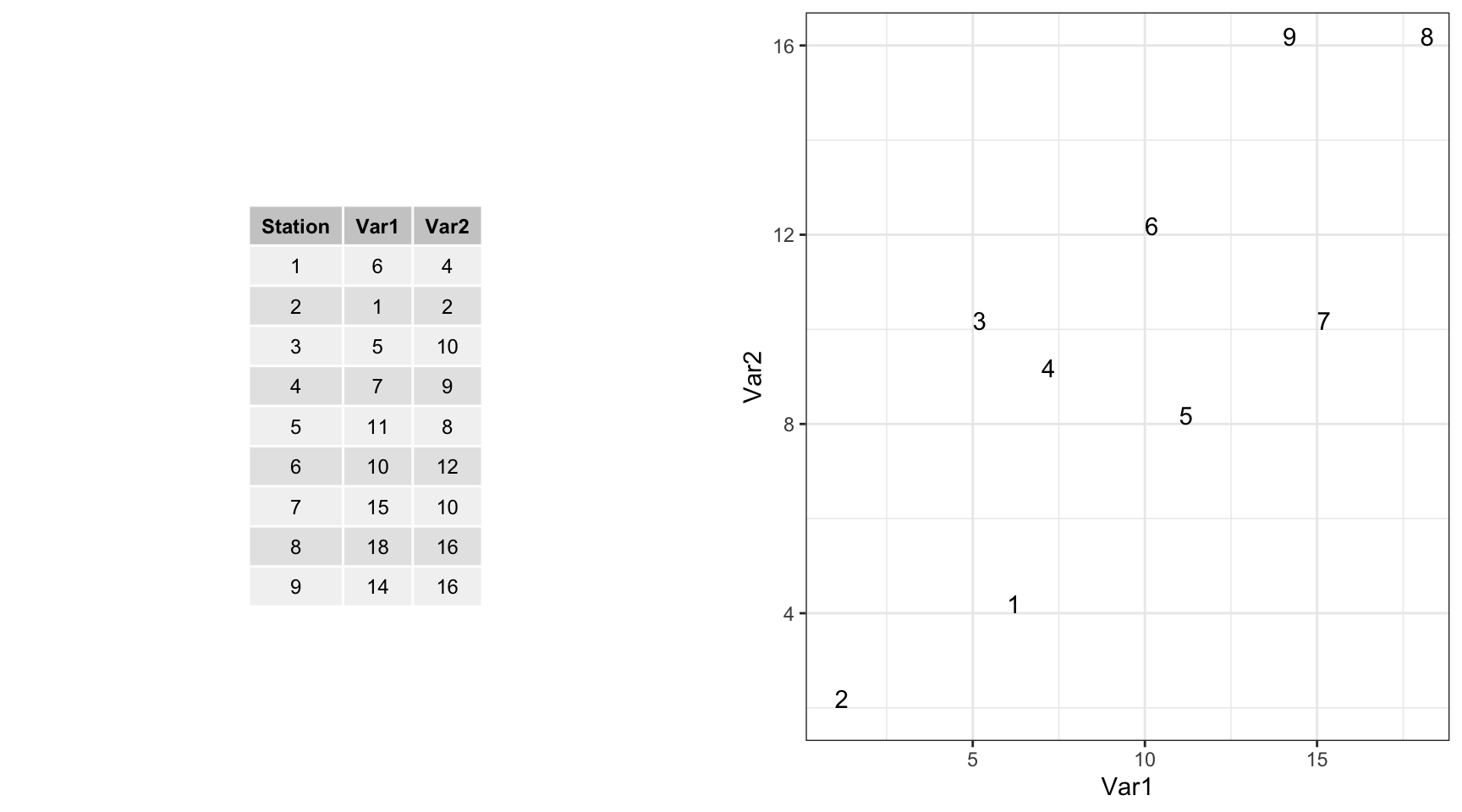
Si nous réduisons à une seule dimension en laissant tomber une des deux variables, voici ce que cela donne (ici on ne garde que Var1, donc, on projette les points sur l’axe des abscisses).
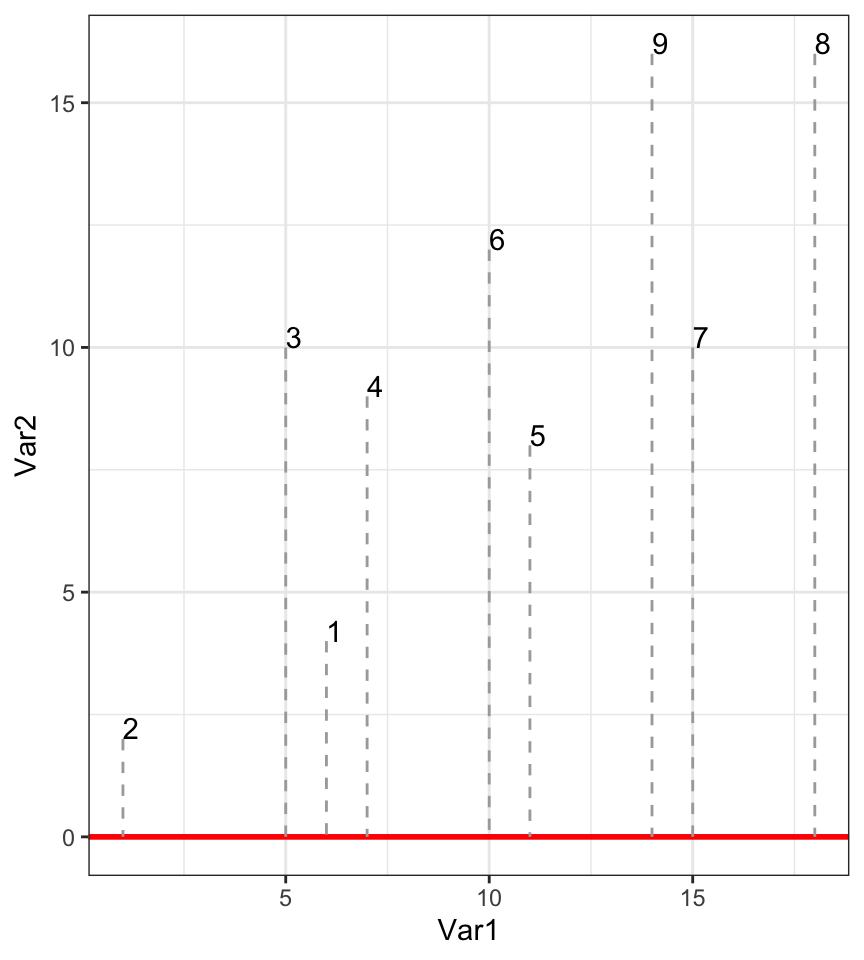
Au final, nous avons ordonné nos individus en une dimension comme suit :
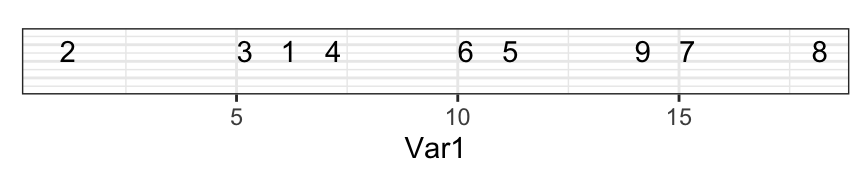
C’est une mauvaise solution car il y a trop de perte d’information. Regardez l’écart entre 7 et 9 sur le graphique en deux dimensions et dans celui à une dimension : les points sont trop près. Comparez sur les deux graphiques les distances 7 - 9 avec 9 - 8 et 1 - 2 versus 1 - 3. Tout cela est très mal représenté en une seule dimension.
Une autre solution serait de projeter le long de la droite de “tendance générale”, c’est-à-dire le long de l’axe de plus grand allongement du nuage de points.
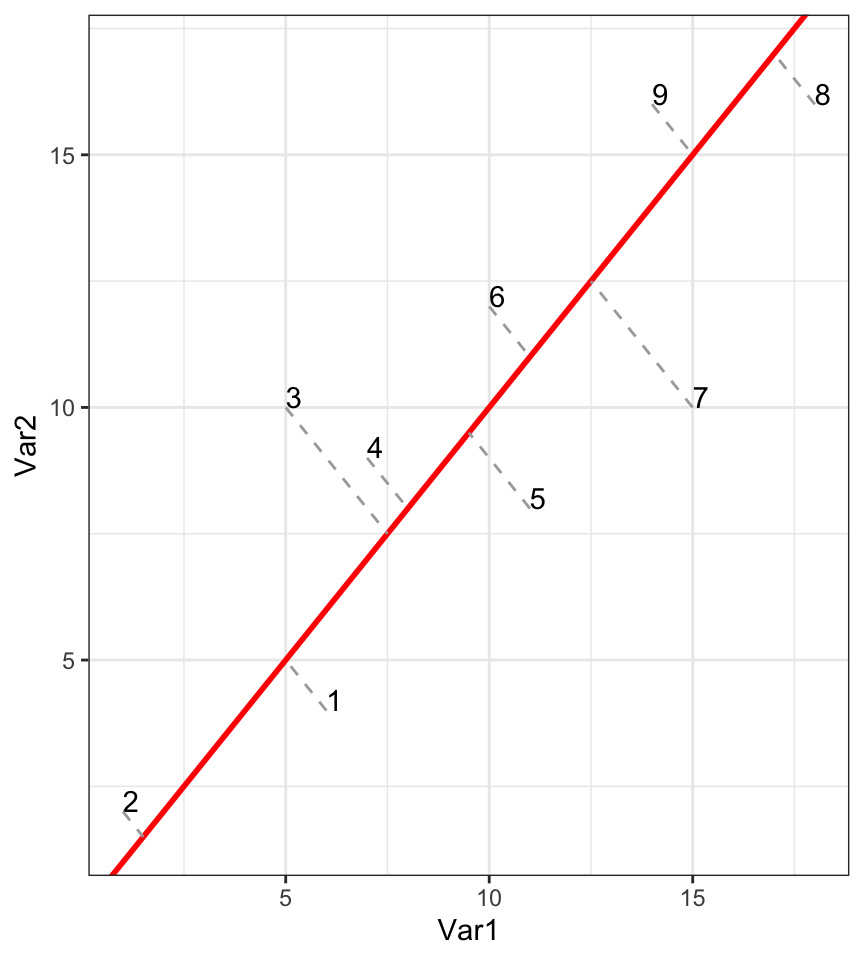
Cela donne ceci en une seule dimension :
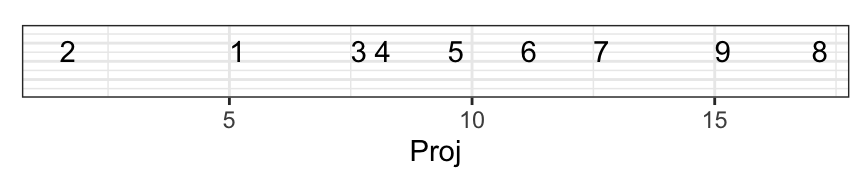
C’est une bien meilleure solution car la perte d’information est ici minimale. Regardez à nouveau la distance entre 7 et 9 sur le graphique initial à deux dimensions et sur le nouveau graphique réduit à une dimension : c’est mieux qu’avant. Comparez aussi les distances respectives entre les paires 7 - 9 et 9 - 8, ainsi que 1 - 2 par rapport à 1 - 3. Tout cela est bien pieux représenté à présent.
L’ACP effectue précisément la projection que nous venons d’imaginer.
La droite de projection est appelée composante principale 1. La composante principale 1 présente la plus grande variabilité possible sur un seul axe.
Ensuite on calcule la composante 2 comme étant orthogonale (i.e., perpendiculaire) à PC1 et présentant la plus grande variabilité non encore capturée par la composante 1.
Le mécanisme revient à projeter les points sur des axes orientés différemment dans l’espace à N dimensions (pour N variables initiales). En effet, mathématiquement ce mécanisme se généralise facilement à trois, puis à N dimensions.
7.1.6 Calcul matriciel ACP
La rotation optimale des axes vers les PC1 à PCN se résout par un calcul matriciel. Nous allons maintenant le détailler. Mais auparavant, nous devons nous rafraîchir l’esprit concernant quelques notions.
Multiplication matricielle : \(\begin{pmatrix} 2 & 3\\ 2 & 1 \end{pmatrix} \times \begin{pmatrix} 1\\ 3 \end{pmatrix} = \begin{pmatrix} 11\\ 5 \end{pmatrix}\)
Vecteurs propres et valeurs propres (il en existe autant qu’il y a de colonnes dans la matrice de départ) :
\[ \begin{pmatrix} 2 & 3\\ 2 & 1 \end{pmatrix} \times \begin{pmatrix} 3\\ 2 \end{pmatrix} = \begin{pmatrix} 12\\ 8 \end{pmatrix} = 4 \times \begin{pmatrix} 3\\ 2 \end{pmatrix} \]
La constante (4) est une valeur propre et la matrice multipliée (à droite) est la matrice des vecteurs propres.
La rotation d’un système d’axes à deux dimensions d’un angle \(\alpha\) peut se représenter sous forme d’un calcul matriciel :
\[ \begin{pmatrix} \cos \alpha & \sin \alpha\\ -\sin \alpha & \cos \alpha \end{pmatrix} \times \begin{pmatrix} x\\ y \end{pmatrix} = \begin{pmatrix} x'\\ y' \end{pmatrix} \]
Dans le cas particulier de l’ACP, la matrice de transformation qui effectue la rotation voulue pour obtenir les axes principaux est la matrice rassemblant tous les vecteurs propres calculés après diagonalisation de la matrice de corrélation ou de variance/covariance (réduction ou non, respectivement). Le schéma suivant visualise la rotation depuis les axes initiaux X et Y (variables de départ) en bleu royal vers les PC1, PC2 en rouge. Un individu p est représenté par les coordonnées {x, y} dans le système d’axes initial XY. Les nouvelles coordonnées {x’, y’} sont recalculées par projection sur les nouveaux axes PC1-PC2. Les flèches bleues sont représentées dans l’espace des variables, tandis que les points reprojetés sur PC1-PC2 sont représentés dans l’espace des individus selon les coordonnées primes en rouge.
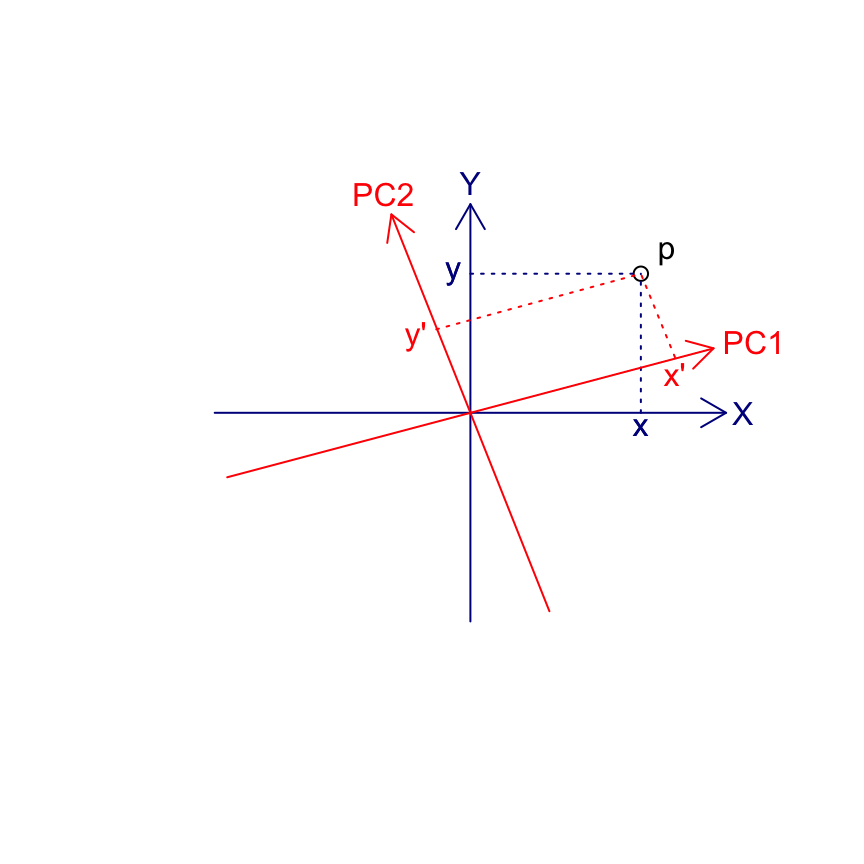
7.1.6.1 Résolution numérique simple
Effectuons une ACP sur matrice var/covar sans réduction des données (mais calcul très similaire lorsque les données sont réduites) sur un exemple numérique simple.
- Étape 1 : centrage des données
\[ \mathop{\begin{pmatrix} 2 & 1 \\ 3 & 4 \\ 5 & 0 \\ 7 & 6 \\ 9 & 2 \end{pmatrix}}_{\text{Tableau brut}} \xrightarrow{\phantom{---}\text{centrage}\phantom{---}} \mathop{\begin{pmatrix} -3.2 & -1.8 \\ -2.2 & \phantom{-}1.4 \\ -0.2 & -2.6 \\ \phantom{-}1.8 & \phantom{-}3.4 \\ \phantom{-}3.8 & -0.6 \end{pmatrix}}_{\text{Tableau centré (X)}} \]
- Étape 2 : calcul de la matrice de variance/covariance
\[ \mathop{\begin{pmatrix} -3.2 & -1.8 \\ -2.2 & \phantom{-}1.4 \\ -0.2 & -2.6 \\ \phantom{-}1.8 & \phantom{-}3.4 \\ \phantom{-}3.8 & -0.6 \end{pmatrix}}_{\text{Tableau centré (X)}} \xrightarrow{\phantom{---}\text{var/covar}\phantom{---}} \mathop{\begin{pmatrix} 8.2 & 1.6 \\ 1.6 & 5.8 \end{pmatrix}}_{\text{Matrice carrée (A)}} \]
- Étape 3 : diagonalisation de la matrice var/covar
\[ \mathop{\begin{pmatrix} 8.2 & 1.6 \\ 1.6 & 5.8 \end{pmatrix}}_{\text{Matrice carrée (A)}} \xrightarrow{\phantom{---}\text{diagonalisation}\phantom{---}} \mathop{\begin{pmatrix} 9 & 0 \\ 0 & 5 \end{pmatrix}}_{\text{Matrice diagonalisée (B)}} \]
La trace des deux matrices A et B (somme des éléments sur la diagonale) est égale à : 8.2 + 5.8 = 14 = 9 + 5.
8.2 est la part de variance exprimée sur le premier axe initial (X)
5.8 est la part de variance exprimée sur le second axe initial (Y)
14 est la variance totale du jeu de données
La matrice diagonale B est la solution exprimant la plus grande part de variance possible sur le premier axe de l’ACP : 9, soit 64,3% de la variance totale.
Les éléments sur la diagonale sont les valeurs propres \(\lambda_i\) ! Vous vous rappelez les fameuses “eigenvalues” dans la sortie de
summary(pima_pca).Étape 4 : calcul de la matrice de rotation des axes (en utilisant la propriété des valeurs propres \(\text{A}.\text{U} = \text{B}.\text{U}\)).
\[ \mathop{\begin{pmatrix} 8.2 & 1.6 \\ 1.6 & 5.8 \end{pmatrix}}_{\text{Matrice A}} \times \text{U} = \mathop{\begin{pmatrix} 9 & 0 \\ 0 & 5 \end{pmatrix}}_{\text{Matrice B}} \times \text{U} \rightarrow \text{U} = \mathop{\begin{pmatrix} \phantom{-}0.894 & -0.447 \\ \phantom{-}0.447 & \phantom{-}0.894 \end{pmatrix}}_{\text{Matrice des vecteur propres (U)}} \]
- La matrice des vecteurs propres (U) (“eigenvectors” en anglais) effectue la transformation (rotation des axes) pour obtenir les composantes principales.
- L’angle de rotation se déduit en considérant que cette matrice contient des sinus et cosinus d’angles de rotation des axes :
\[ \begin{pmatrix} \phantom{-}0.894 & -0.447 \\ \phantom{-}0.447 & \phantom{-}0.894 \end{pmatrix} = \begin{pmatrix} \phantom{-}\cos(-26.6°) & \phantom{-}\sin(-26.6°) \\ -\sin(-26.6°) & \phantom{-}\cos(-26.6°) \end{pmatrix} \]
Étape 5 : représentation dans l’espace des variables. C’est une représentation dans un cercle de la matrice des vecteurs propres U sous forme de vecteurs.
Étape 6 : représentation dans l’espace des individus. On recalcule les coordonnées des individus dans le système d’axe après rotation.
\[ \mathop{\begin{pmatrix} -3.2 & -1.8 \\ -2.2 & \phantom{-}1.4 \\ -0.2 & -2.6 \\ \phantom{-}1.8 & \phantom{-}3.4 \\ \phantom{-}3.8 & -0.6 \end{pmatrix}}_{\text{Tableau centré (X)}} \times \mathop{\begin{pmatrix} \phantom{-}0.894 & -0.447 \\ \phantom{-}0.447 & \phantom{-}0.894 \end{pmatrix}}_{\text{Matrice des vecteur propres (U)}} \xrightarrow{\phantom{---}\text{X}.\text{U} = \text{X'}\phantom{---}} \mathop{\begin{pmatrix} -3.58 & \phantom{-}0.00 \\ -1.34 & \phantom{-}2.24 \\ -1.34 & -2.24 \\ \phantom{-}3.13 & \phantom{-}2.24 \\ \phantom{-}3.13 & -2.24 \end{pmatrix}}_{\text{Tableau avec rotation (X')}} \]
- Ensuite, on représente ces individus à l’aide d’un graphique en nuage de points.
Tout ces calculs se généralisent facilement à trois, puis à N dimensions.
À vous de jouer !
Effectuez maintenant les exercices du tutoriel B07La_pca (Analyse en composantes principales).
BioDataScience2::run("B07La_pca")Réalisez le travail B07Ia_acp_afc, partie I.
Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques II à l’UMONS (Q2 : analyse) à terminer avant le 2022-03-21 23:59:59.
Initiez votre projet GitHub Classroom
Voyez les explications dans le fichier README.md, partie I.
Pour aller plus loin
N’hésitez pas à combiner plusieurs techniques. Par exemple, vous pouvez représenter les groupes créés par classification ascendante hiérarchiques sur un graphique de l’ACP dans l’espace des individus en faisant varier les couleurs ou les labels des individus en fonction des groupes de la CAH.
Une autre explication de l’ACP en utilisant quelques autres fonctions de R pour visualiser le résultat
Une page qui reprend une série de vidéos qui présentent les différentes facettes de l’ACP (en anglais).