3.3 Matrice de contraste

La version que nous avons étudié jusqu’ici pour nos variables indicatrices, à savoir, une seule prend la valeur 1 lorsque toutes les autres prennent une valeur zéro, n’est qu’un cas particulier de ce qu’on appelle les contrastes appliqués à ces variables indicatrices. En réalité, nous pouvons leurs donner bien d’autres valeurs (on parle de poids), et cela permettra de considérer des contrastes différents, eux-mêmes représentatifs de situations différentes.

Afin de mieux comprendre les contrastes appliqués à nos modèles linéaires, les statisticiens ont inventé les matrices de contrastes. Ce sont des tableaux à deux entrées indiquant pour chaque niveau de la variable indépendante qualitative quelles sont les valeurs utilisées pour les différentes variables indicatrices présentées en colonne.

Dans le cas de notre version simplifiée du modèle mathématique où nous avons fait disparaître \(I_1\) en l’assimilant à la moyenne \(\mu\) pour obtenir \(\beta_1\). Dans le cas où notre variable qualitative a quatre niveaux, nous avons donc le modèle suivant :

\[ y = \beta_1 + \beta_2 I_2 + \beta_3 I_3 + \beta_4 I_4 + \epsilon \]

Cela revient à considérer le premier niveau comme niveau de référence et à établir tous les contrastes par rapport à ce niveau de référence. C’est une situation que l’on rencontre fréquemment lorsque nos testons l’effet de différents médicaments ou de différents traitement par rapport à un contrôle (pas de traitement, ou placebo). La matrice de contrastes correspondante, dans un cas où on aurait trois traitements en plus du contrôle (donc, notre variable factor à quatre niveaux) s’obtient facilement dans R à l’aide de la fonction contr.treatment() :

contr.treatment(4)

#   2 3 4
# 1 0 0 0
# 2 1 0 0
# 3 0 1 0
# 4 0 0 1

Les lignes de cette matrice sont numérotées de 1 à 4. Elles correspondent aux quatre niveaux de notre variable factor, avec le niveau 1 qui doit nécessairement correspondre à la situation de référence, donc au contrôle.

Les colonnes de cette matrice correspondent aux trois variables indicatrices \(I_1\), \(I_2\) et \(I_3\) de l’équation au dessus. Nous voyons que pour une individu contrôle, de niveau 1, les trois \(I_i\) prennent la valeur 0. Nous sommes bien dans la situation de référence. En d’autres terme, le modèle de base est ajusté sur la moyenne des individus contrôle. Notre modèle se réduit à : \(y = \beta_1 + \epsilon\). Donc, seule la moyenne des individus contrôles, \(\beta_1\) est considérée, en plus des résidus \(\epsilon\) bien sûr.

Pour le niveau deux, nous observons que \(I_2\) vaut 1 et les deux autres \(I_i\) valent 0. Donc, cela revient à considérer un décalage constant \(\beta_2\) appliqué par rapport au modèle de référence matérialisé par \(\beta_1\). En effet, notre équation se réduit dans ce cas à : \(y = \beta_1 + \beta_2 + \epsilon\).

Le même raisonnement peut être fait pour les niveaux 3 et 4, avec des décalages constants par rapport à la situation contrôle de respectivement \(\beta_3\) et \(\beta_4\).

En d’autres termes, les contrastes qui sont construits ici font tous référence au contrôle, et chaque médicament est explicitement comparé au contrôle (mais les médicaments ne sont pas comparés entre eux). Nous voyons donc que les variables indicatrices et la matrice de contrastes permettent de spécifier quelles sont les contrastes pertinents et éliminent ceux qui ne le sont pas (nous n’utilisons donc pas systématiquement toutes les comparaisons deux à deux des différents niveaux⁶).

3.3.1 Contraste orthogonaux

Les contrastes doivent être de préférence orthogonaux par rapport à l’ordonnée à l’origine, ce qui signifie que la somme de leurs pondérations doit être nulle pour tous les contrastes définis (donc, en colonnes). Bien que n’étant pas obligatoire, cela confère des propriétés intéressantes au modèle (l’explication et la démonstration sortent du cadre de ce cours). Or, les contrastes de type traitement ne sont pas orthogonaux puisque toutes les sommes par colonnes vaut un.

3.3.2 Autres matrices de contrastes courantes

• Somme à zéro. Ces contrastes, toujours pour une variable à quatre niveaux, se définissent comme suit en utilisant la fonction contr.sum() dans R :

contr.sum(4)

#   [,1] [,2] [,3]
# 1    1    0    0
# 2    0    1    0
# 3    0    0    1
# 4   -1   -1   -1

Ici nous avons bien des contrastes orthogonaux puisque toutes les sommes par colonnes valent zéro. Dans le cas présent, aucun niveau n’est considéré comme référence, mais les n - 1 niveaux sont systématiquement contrastés avec le dernier et nîème^ niveau. Ainsi, un contraste entre deux niveaux particuliers peut s’élaborer en indiquant une pondération de 1 pour le premier niveau à comparer, une pondération de -1 pour le second à comparer et une pondération de 0 pour tous les autres.

• Matrice de contrastes de Helmert : chaque niveau est comparé à la moyenne des niveaux précédents. La matrice de contrastes correspondant pour une variable à quatre niveaux s’obtient à l’aide de la fonction R contr.helmert() :

contr.helmert(4)

#   [,1] [,2] [,3]
# 1   -1   -1   -1
# 2    1   -1   -1
# 3    0    2   -1
# 4    0    0    3

Cette matrice est également orthogonale avec toutes les sommes par colonnes qui valent zéro. Ici, nous découvrons qu’il est possible de créer un contraste entre un niveau et la moyenne de plusieurs autres niveaux en mettant le poids du premier à m (le nombre de populations à comparer de l’autre côté du contraste), et les poids des autres populations tous à -1. Ainsi, la colonne 4 compare le niveau quatre avec pondération 3 aux trois autres niveaux qui reçoivent tous une pondération -1.

• Matrice de contrastes polynomiaux : adapté aux facteurs ordonnés (ordered dans R) pour lesquels on s’attend à une certaine évolution du modèle du niveau le plus petit au plus grand.

Donc ici aussi une comparaison deux à deux de tous les niveaux n’est pas souhaitable, mais une progression d’un effet qui se propage de manière graduelle du plus petit niveau au plus grand. A priori cela parait difficile à matérialiser dans une matrice de contraste… et pourtant, c’est parfaitement possible ! Il s’agit de contrastes polynomiaux où nous ajustons de polynômes de degré croissant comme pondération des différents contrastes étudiés. La fonction contr.poly() permet d’obtenir ce type de contraste dans R. Pour une variable ordonnée à quatre niveaux, cela donne :

contr.poly(4)

#              .L   .Q         .C
# [1,] -0.6708204  0.5 -0.2236068
# [2,] -0.2236068 -0.5  0.6708204
# [3,]  0.2236068 -0.5 -0.6708204
# [4,]  0.6708204  0.5  0.2236068

Ici, les pondérations sont plus difficiles à expliquer rien qu’en observant la matrice de contrastes. De plus, les colonnes portent ici des noms particuliers .L pour un contraste linéaire (polynôme d’ordre 1), .Q pour un contraste quadratique (polynôme d’ordre 2), et .C pour un contraste conique (ou polynôme d’ordre 3). Les pondérations appliquées se comprennent mieux lorsqu’on augmente le nombre de niveaux et que l’on représente graphiquement la valeur des pondérations choisies. Par exemple, pour une variable facteur ordonnée à dix niveaux, nous représentons graphiquement les 3 premiers contrastes (linéaire, quadratique et conique) comme suit :

plot(contr.poly(10)[, 1], type = "b")

plot(contr.poly(10)[, 2], type = "b")

plot(contr.poly(10)[, 3], type = "b")

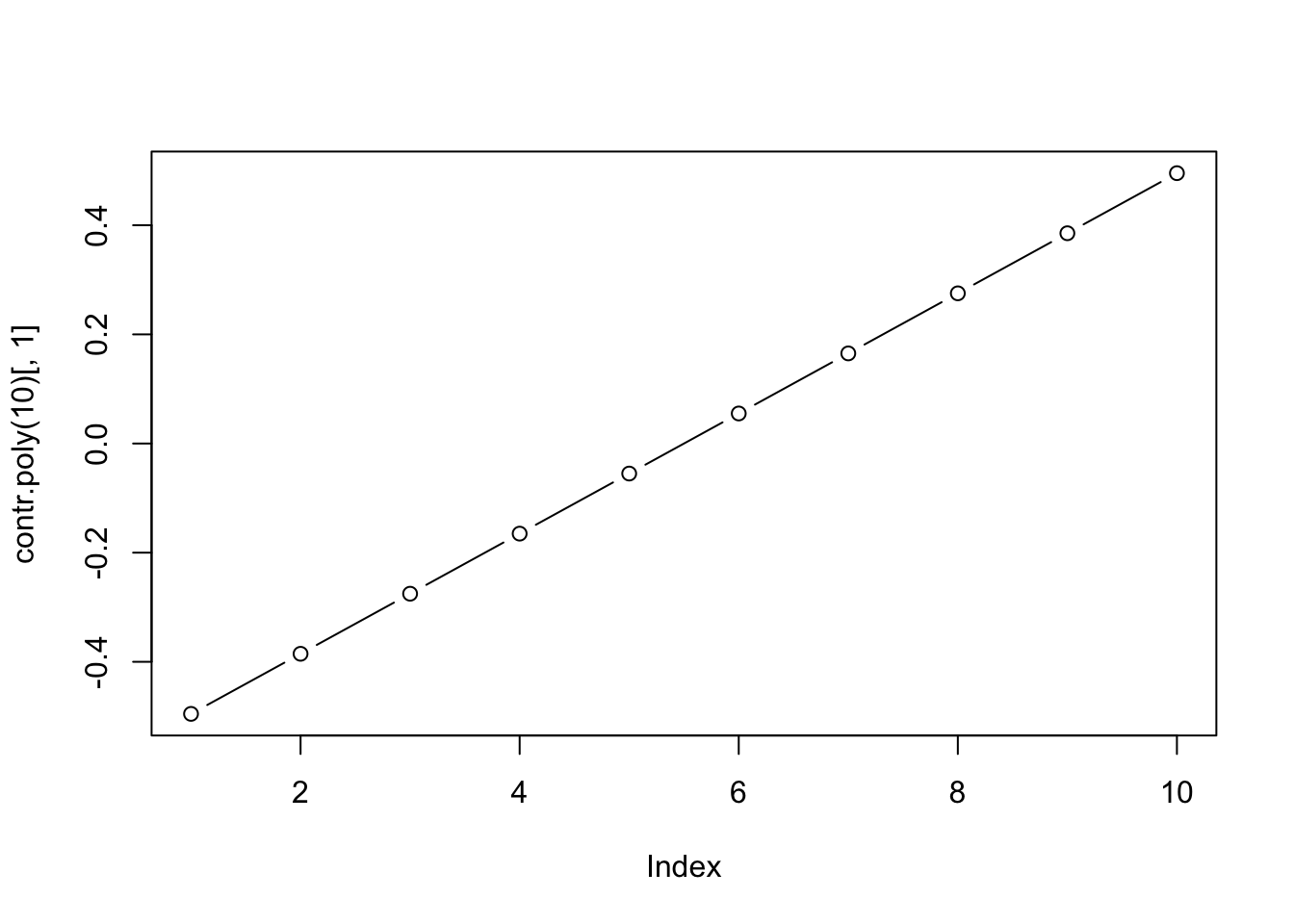
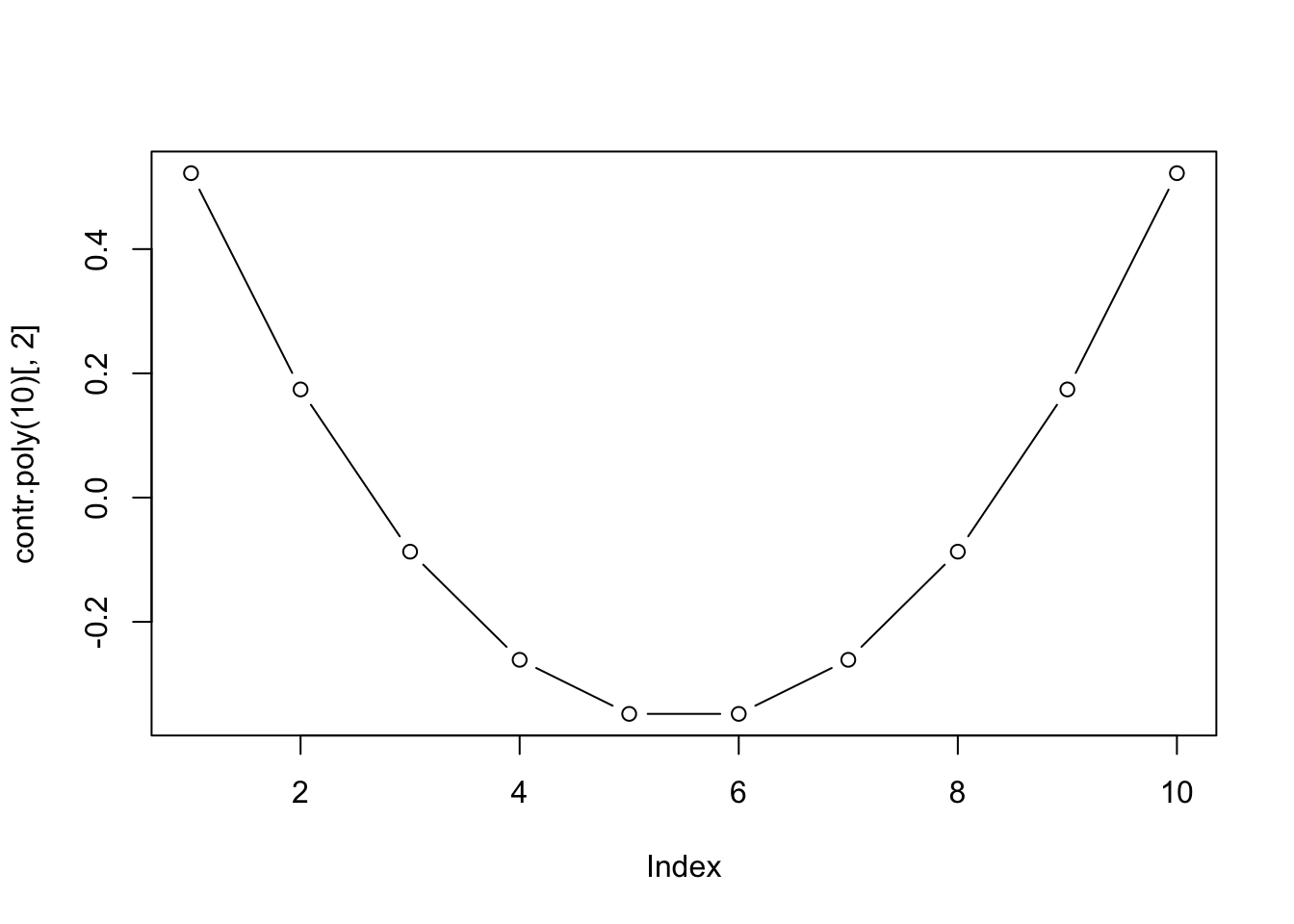
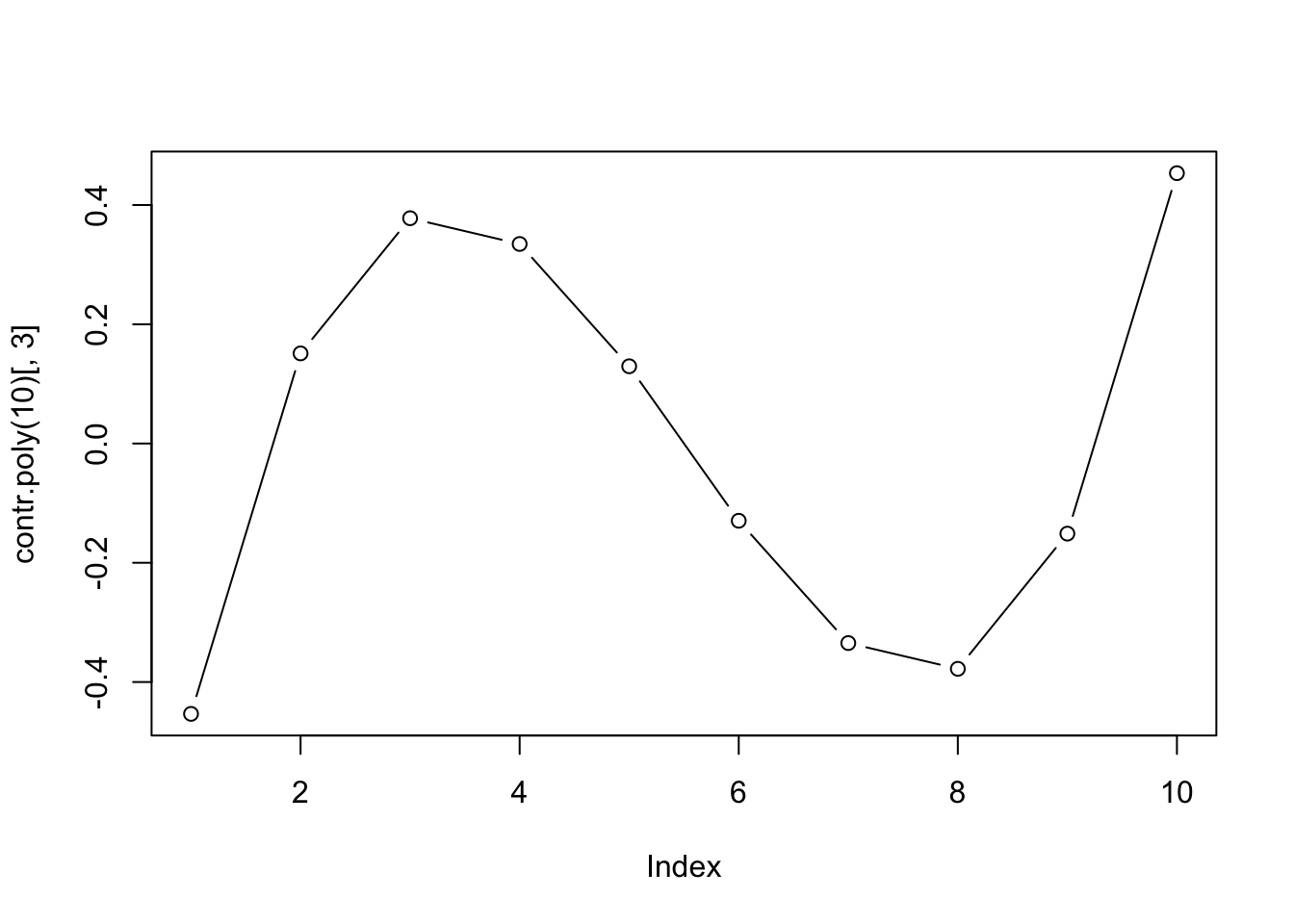
Sur le graphique, l’axe X nommé index correspond en réalité à la succession des dix niveaux de la variable présentés dans l’ordre du plus petit au plus grand. Nous voyons maintenant clairement comment les contrastes sont construits ici. Pour le contraste linéaire, on contraste les petits niveaux avec les grands, et ce, de manière proportionnelle par rapport à la progression d’un niveau à l’autre (polynôme d’ordre un = droite). Pour le contraste quadratique, on place “dans le même sac” les petits et grand niveaux qui sont contrastés avec les niveaux moyens (nous avons une parabole ou polynôme d’ordre deux). Pour le troisième graphique, la situation se complexifie en encore un peu plus avec un polynôme d’ordre trois, et ainsi de suite pour des polynômes d’ordres croissants jusqu’à remplir complètement la matrice de contrastes.

R utilise par défaut des contrastes de traitement pour les facteurs non ordonnés et des contrastes polynomiaux pour des facteurs ordonnés. Ces valeurs par défaut sont stockées dans l’option contrasts que l’on peut lire à l’aide de getOption().

Bien sûr, il est possible de changer ces contrastes, tant au niveau global qu’au niveau de la construction d’un modèle en particulier.

getOption("contrasts")

#         unordered           ordered 
# "contr.treatment"      "contr.poly"