6.3 Cartes auto-adaptatives (SOM)
Le positionnement multidimensionnel faisant appel à une matrice de distances entre tous les individus, les calculs deviennent vite pénalisants au fur et à mesure que le jeu de données augmente en taille. En général, les calculs sont assez lents. Nous verrons au module suivant que l’analyse en composantes principales apporte une réponse intéressante à ce problème, mais nous contraint à étudier des corrélations linéaires et des distances de type euclidiennes.
Une approche radicalement différente, qui reste plus générale car non linéaire, est la méthode des cartes auto-adaptatives, ou encore, cartes de Kohonen du nom de son auteur se désigne par “self-organizing map” en anglais. L’acronyme SOM est fréquemment utilisé, même en français. Cette technique va encore une fois exploiter une matrice de distances dans le but de représenter les individus sur une carte. Cette fois-ci, la carte contient un certain nombre de cellules qui forment une grille, ou mieux, une disposition en nid d’abeille (nous verrons plus loin pourquoi cette disposition particulière est intéressante). De manière similaire au MDS, nous allons faire en sorte que des individus similaires soient proches sur la carte, et des individus différents soient éloignés. La division de la carte en différentes cellules permet de regrouper les individus. Ceci permet une classification comme pour la CAH ou les k-moyennes. Les SOM apparaissent donc comme une technique hybride entre ordination (représentation sur des cartes) et classification (regroupement des individus).
À vous de jouer !
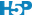
La théorie et les calculs derrière les SOM sont très complexes. Elles font appel aux réseaux de neurones adaptatifs et leur fonctionnement est inspiré de celui du cerveau humain. Tout comme notre cerveau, les SOM vont utiliser l’information en entrée pour aller assigner une zone de traitement de l’information (pour notre cerveau) ou une cellule dans la carte (pour les SOM). Étant donné la complexité du calcul, les développement mathématiques n’ont pas leur place dans ce cours. Ce qui importe, c’est de comprendre le concept, et d’être ensuite capable d’utiliser les SOM à bon escient. Uniquement pour ceux d’entre vous qui désirent comprendre les détails du calcul, vous pouvez lire ici ou visionner la vidéo suivante (facultative et en anglais) :
Plutôt que de détailler les calculs, nous vous montrons ici comment un ensemble de pixels de couleurs différentes est organisé sur une carte SOM de Kohonen en un arrangement infiniment plus cohérent… automatiquement (cet exemple est proposé par Frédéric De Lène Mirouze dans son blog).
Ce qui est évident sur un exemple aussi visuel que celui-ci fonctionne aussi très bien pour ranger les individus dans un tableau multivarié a priori chaotique comme ceux que nous rencontrons régulièrement en statistiques multivariées en biologie.
6.3.1 SOM sur le zooplancton
Reprenons notre exemple du zooplancton.
# # A tibble: 1,262 x 20
# ecd area perimeter feret major minor mean mode min max std_dev range
# <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
# 1 0.770 0.465 4.45 1.32 1.16 0.509 0.363 0.036 0.004 0.908 0.231 0.904
# 2 0.700 0.385 2.32 0.728 0.713 0.688 0.361 0.492 0.024 0.676 0.183 0.652
# 3 0.815 0.521 4.15 1.33 1.11 0.598 0.308 0.032 0.008 0.696 0.204 0.688
# 4 0.785 0.484 4.44 1.78 1.56 0.394 0.332 0.036 0.004 0.728 0.218 0.724
# 5 0.361 0.103 1.71 0.739 0.694 0.188 0.153 0.016 0.008 0.452 0.110 0.444
# 6 0.832 0.544 5.27 1.66 1.36 0.511 0.371 0.02 0.004 0.844 0.268 0.84
# 7 1.23 1.20 15.7 3.92 1.37 1.11 0.217 0.012 0.004 0.784 0.214 0.78
# 8 0.620 0.302 3.98 1.19 1.04 0.370 0.316 0.012 0.004 0.756 0.246 0.752
# 9 1.19 1.12 15.3 3.85 1.34 1.06 0.176 0.012 0.004 0.728 0.172 0.724
# 10 1.04 0.856 7.60 1.89 1.66 0.656 0.404 0.044 0.004 0.88 0.264 0.876
# # … with 1,252 more rows, and 8 more variables: size <dbl>, aspect <dbl>,
# # elongation <dbl>, compactness <dbl>, transparency <dbl>, circularity <dbl>,
# # density <dbl>, class <fct>Les 19 premières colonnes représentent des mesures réalisées sur notre plancton et la vingtième est la classe. Nous nous débarrasserons de la colonne classe et transformons les données numériques en matrice après avoir standardisé les données (étapes obligatoires) pour stocker le résultat dans zoo_mat.
Avant de pouvoir réaliser notre analyse, nous devons décider d’avance la topologie de la carte, c’est-à-dire, l’arrangement des cellules ainsi que le nombre de lignes et de colonnes. Le nombre de cellules totales choisies dépend à la fois du niveau de détails souhaité, et du nombre d’individus dans votre jeu de données (il faut naturellement plus de données que de cellules, disons, au moins 5 à 10 fois plus). Pour l’instant, considérons les deux topologies les plus fréquentes : la grille rectangulaire et la grille hexagonale. Plus le nombre de cellules est important, plus la carte sera détaillée, mais plus il nous faudra de données pour la calculer et la “peupler”. Considérons par exemple une grille 7 par 7 qui contient donc 49 cellules au total. Sachant que nous avons plus de 1200 particules de plancton mesurées dans zoo, le niveau de détail choisi est loin d’être trop ambitieux.
La grille rectangulaire est celle qui vous vient probablement immédiatement à l’esprit. Il s’agit d’arranger les cellules en lignes horizontales et colonnes verticales. La fonction somgrid() du package {kohonen} permet de créer une telle grille.
#
# Attachement du package : 'kohonen'# The following object is masked from 'package:purrr':
#
# mapIl n’y a pas de graphique chart ou ggplot2 dans le package {kohonen}. Nous utiliserons ici les graphiques de base de R. Pour visualiser la grille, il faut la transformer en un objet kohonen. Nous pouvons ajouter plein d’information sur la grille. Ici, nous rajoutons une propriété calculée à l’aide de unit.distances() qui est la distance des cellules de la carte par référence à la cellule centrale. Les cellules sont numérotées de 1 à n en partant en bas à gauche, en progressant le long de la ligne du bas vers la droite, et en reprenant à gauche à la ligne au dessus. Donc, la ligne du bas contient de gauche à droite les cellules n°1 à 7. La ligne au dessus contient les cellules n°8 à 14, et ainsi de suite. La cellule du centre de la grille en en quatrième ligne en partant du bas et en position 4 sur cette ligne, soit trois lignes complètes plus quatre (\(3*7+4=25\)). C’est la cellule n°25.
rect_grid_7_7 %>.%
# Transformation en un objet de classe kohonen qui est une liste
structure(list(grid = .), class = "kohonen") %>.% # Objet de classe kohonen
plot(., type = "property", # Graphique de propriété
property = unit.distances(rect_grid_7_7)[25, ], # distance à la cellule 25
main = "Distance depuis la cellule centrale") # Titre du graphique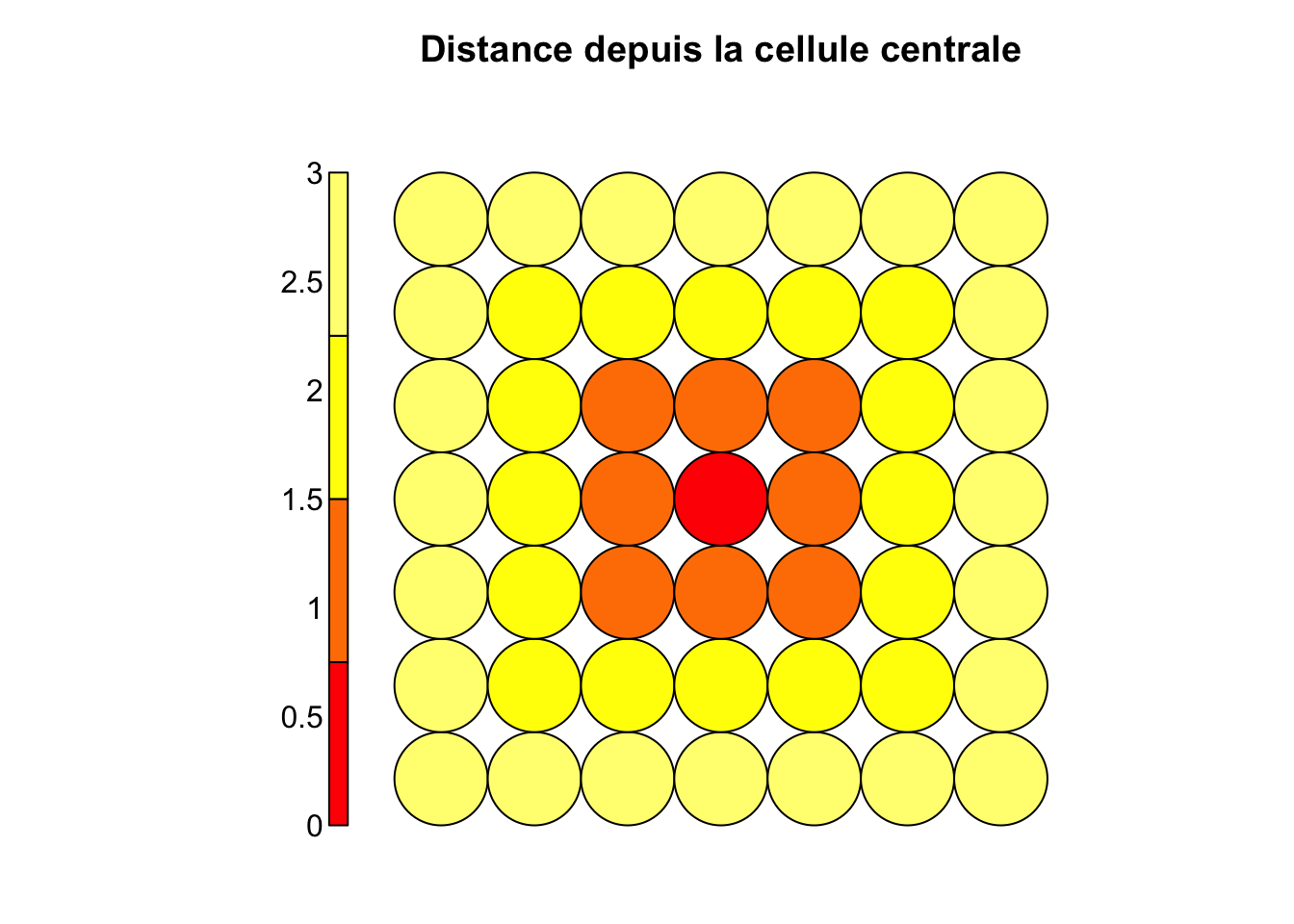
Les cellules de la grille ne sont pas disposées au hasard dans la carte SOM. Des relations de voisinage sont utilisées pour placer les individus à représenter dans des cellules adjacentes s’ils se ressemblent. Avec une grille rectangulaire, nous avons donc deux modalités de variation : en horizontal et en vertical, ce qui donne deux gradients possibles qui, combinés donnent des extrêmes dans les coins opposés. Une cellule possède huit voisins directs.
L’autre topologie possible est la grille hexagonale. Voyons ce que cela donne :
hex_grid_7_7 <- somgrid(7, 7, topo = "hexagonal")
hex_grid_7_7 %>.%
# Transformation en un objet de classe kohonen qui est une liste
structure(list(grid = .), class = "kohonen") %>.% # Objet de classe kohonen
plot(., type = "property", # Graphique de propriété
property = unit.distances(hex_grid_7_7)[25, ], # distance à la cellule 25
main = "Distance depuis la cellule centrale") # Titre du graphique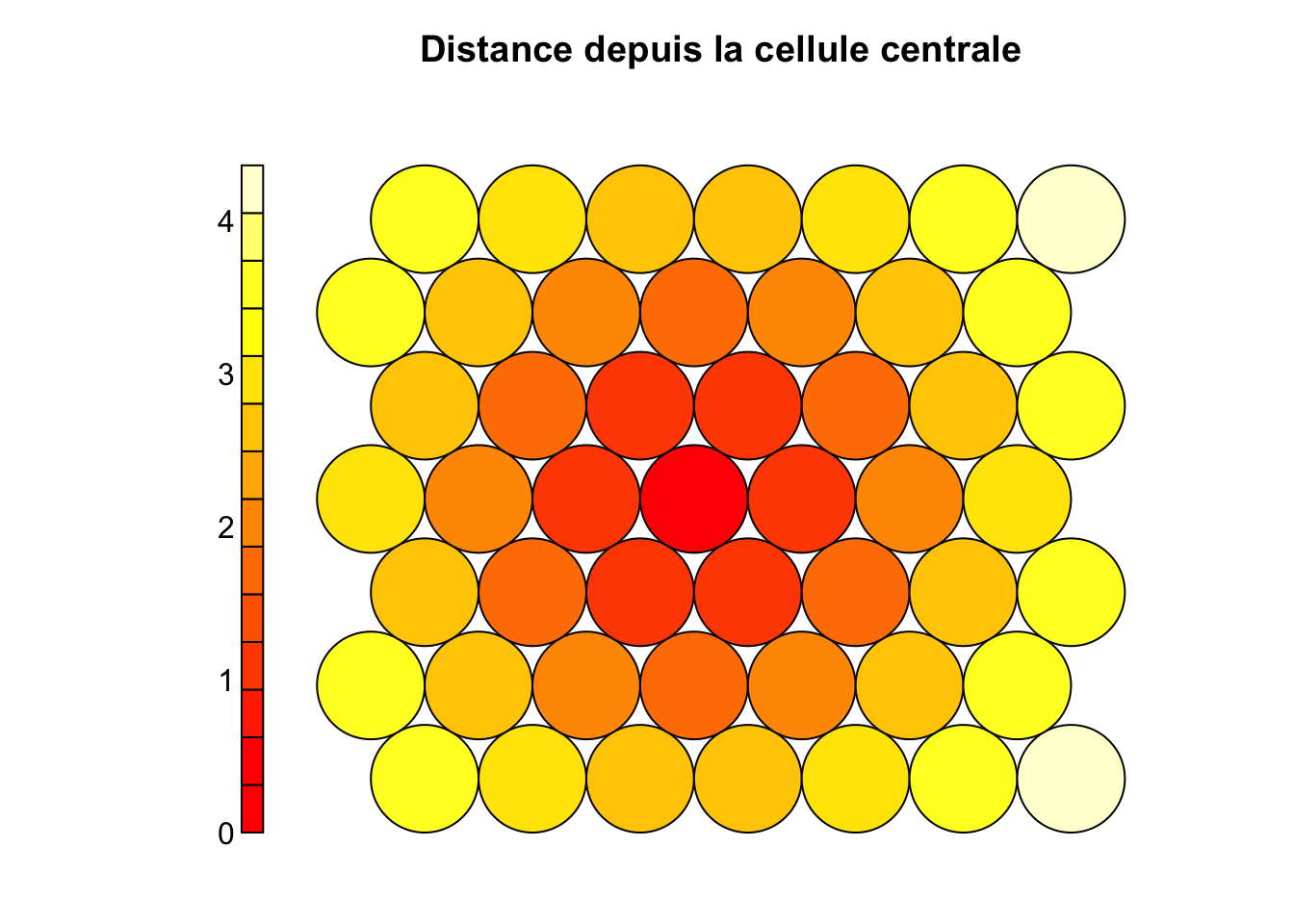
Ici, nous n’avons que six voisins directs, mais trois directions dans lesquelles les gradients peuvent varier : en horizontal, en diagonale vers la gauche et en diagonale vers la droite. Cela offre plus de possibilités pour l’agencement des individus. Nous voyons aussi plus de nuances dans les distances (il y a plus de couleurs différentes) pour une grille de même taille 7 par 7 que dans le cas de la grille rectangulaire. Nous utiliserons donc préférentiellement la grille hexagonale.
Effectuons maintenant le calcul de notre SOM à l’aide de la fonction som() du package {kohonen}. Comme l’analyse fait intervenir le générateur pseudo-aléatoire, nous pouvons utiliser de manière optionnelle set.seed() avec un nombre choisi au hasard (et toujours différent à chaque utilisation) pour que cette analyse particulière-là soit reproductible. Sinon, à chaque exécution, nous obtiendrons un résultat légèrement différent.
# SOM of size 7x7 with a hexagonal topology and a bubble neighbourhood function.
# The number of data layers is 1.
# Distance measure(s) used: sumofsquares.
# Training data included: 1262 objects.
# Mean distance to the closest unit in the map: 2.547.Le résumé de l’objet ne nous donne pas beaucoup d’info. C’est normal. La technique étant visuelle, ce sont les représentations graphiques qui sont à utiliser ici. Avec les graphiques R de base, la fonction utilisée est plot(). Nous avons plusieurs types disponibles et une large palette d’options. Voyez l’aide en ligne de?plot.kohonen. Le premier graphique (type = "changes") montre l’évolution de l’apprentissage au fil des itérations. L’objectif est de descendre le plus possible sur l’axe des ordonnées pour réduire au maximum la distance des individus par rapport aux cellules (“units” en anglais) où ils devraient se placer. Idéalement, nous souhaitons tendre vers zéro. En pratique, nous pourrons arrêter les itérations lorsque la courbe ne diminue plus de manière significative.
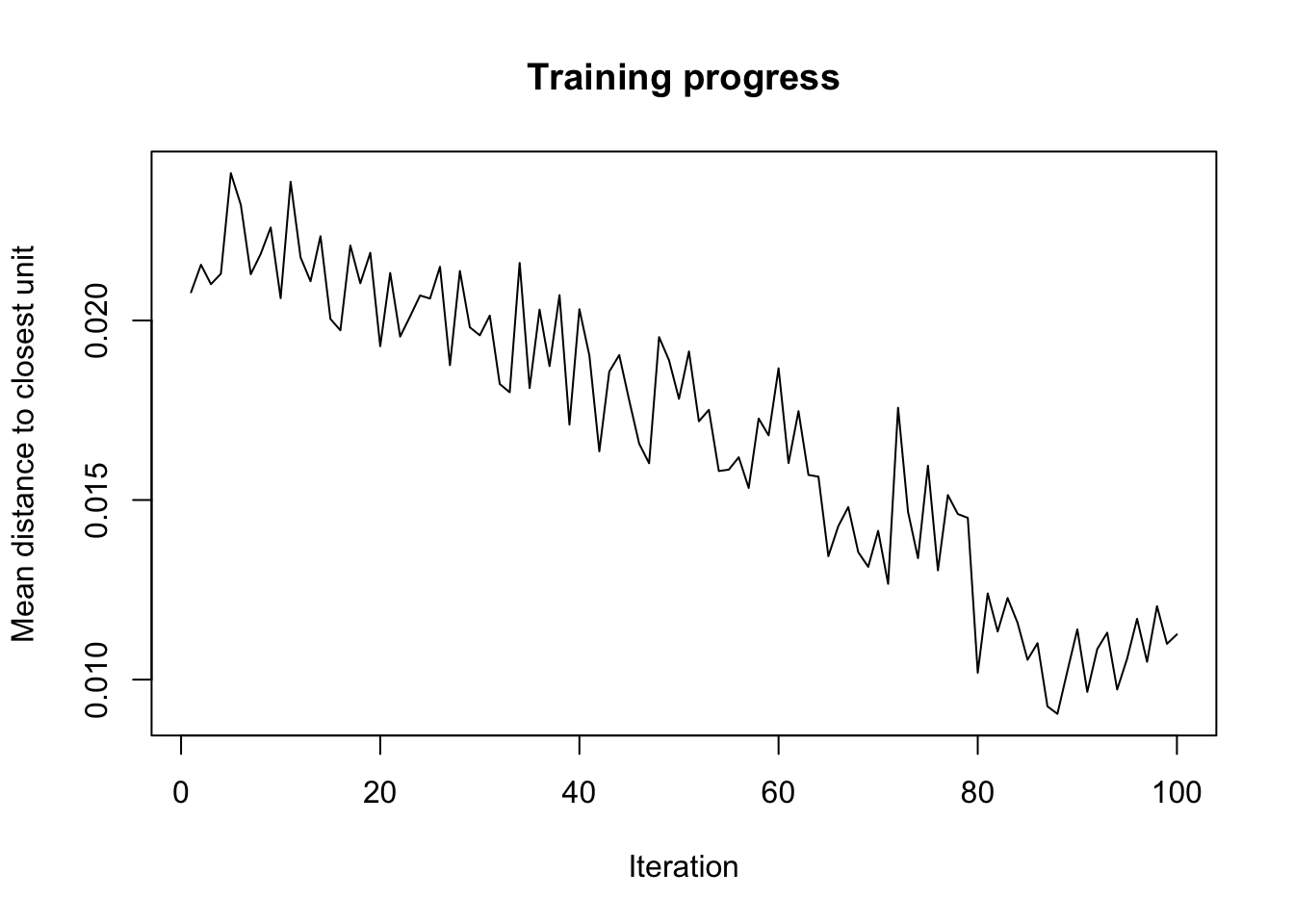
Ici, il semble que nous ne diminuons plus vraiment à partir de l’itération 85 environ. Nous pouvons nous en convaincre en relançant l’analyse avec un plus grand nombre d’itérations (avec l’argument rlen = de som()).
set.seed(954)
zoo_som <- som(zoo_mat, grid = somgrid(7, 7, topo = "hexagonal"), rlen = 200)
plot(zoo_som, type = "changes")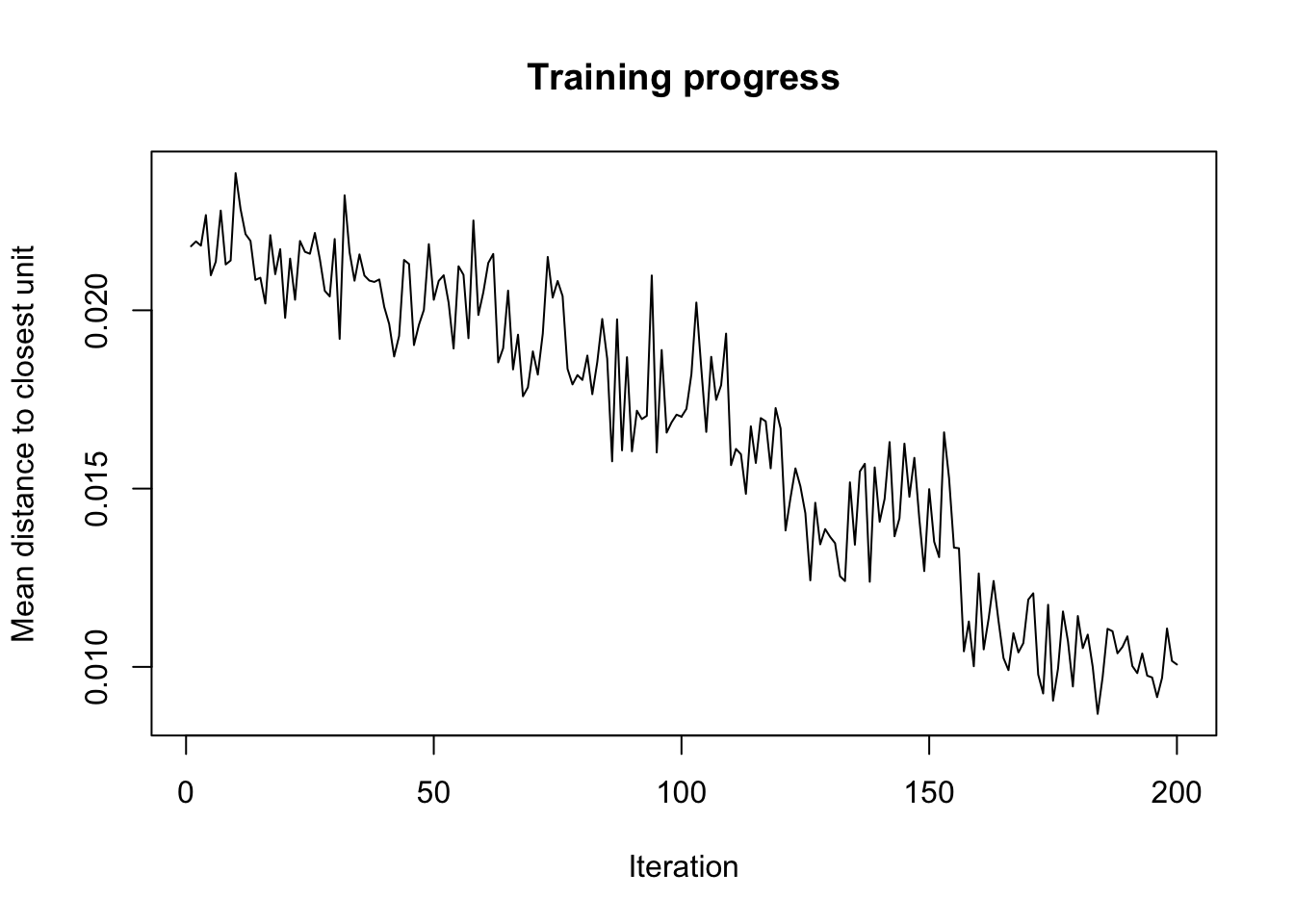
Vous serez sans doute surpris de constater que la diminution de la courbe se fait plus lentement maintenant. En fait som() va adapter son taux d’apprentissage en fonction du nombre d’itérations qu’on lui donne et va alors “peaufiner le travail” d’autant plus. Au final, la valeur n’est pas plus basse pour autant. Donc, nous avons aboutit probablement à une solution.
Le second graphique que nous pouvons réaliser consiste à placer les individus dans la carte, en utilisant éventuellement une couleur différente en fonction d’une caractéristique de ces individus (ici, leur classe). Ce graphique est obtenu avec type = "mapping". Si vous ne voulez pas représenter la grille hexagonale à l’aide de cercles, vous pouvez spécifier shape = "straight". Nous avons 17 classes de zooplancton et il est difficile de représenter plus de 10-12 couleurs distinctes, mais ce site propose une palette de 20 couleurs distinctes. Nous en utiliserons les 17 premières…
colors17 <- c("#e6194B", "#3cb44b", "#ffe119", "#4363d8", "#f58231", "#911eb4",
"#42d4f4", "#f032e6", "#bfef45", "#fabebe", "#469990", "#e6beff", "#9A6324",
"#fffac8", "#800000", "#aaffc3", "#808000", "#ffd8b1")
plot(zoo_som, type = "mapping", shape = "straight", col = colors17[zoo$class])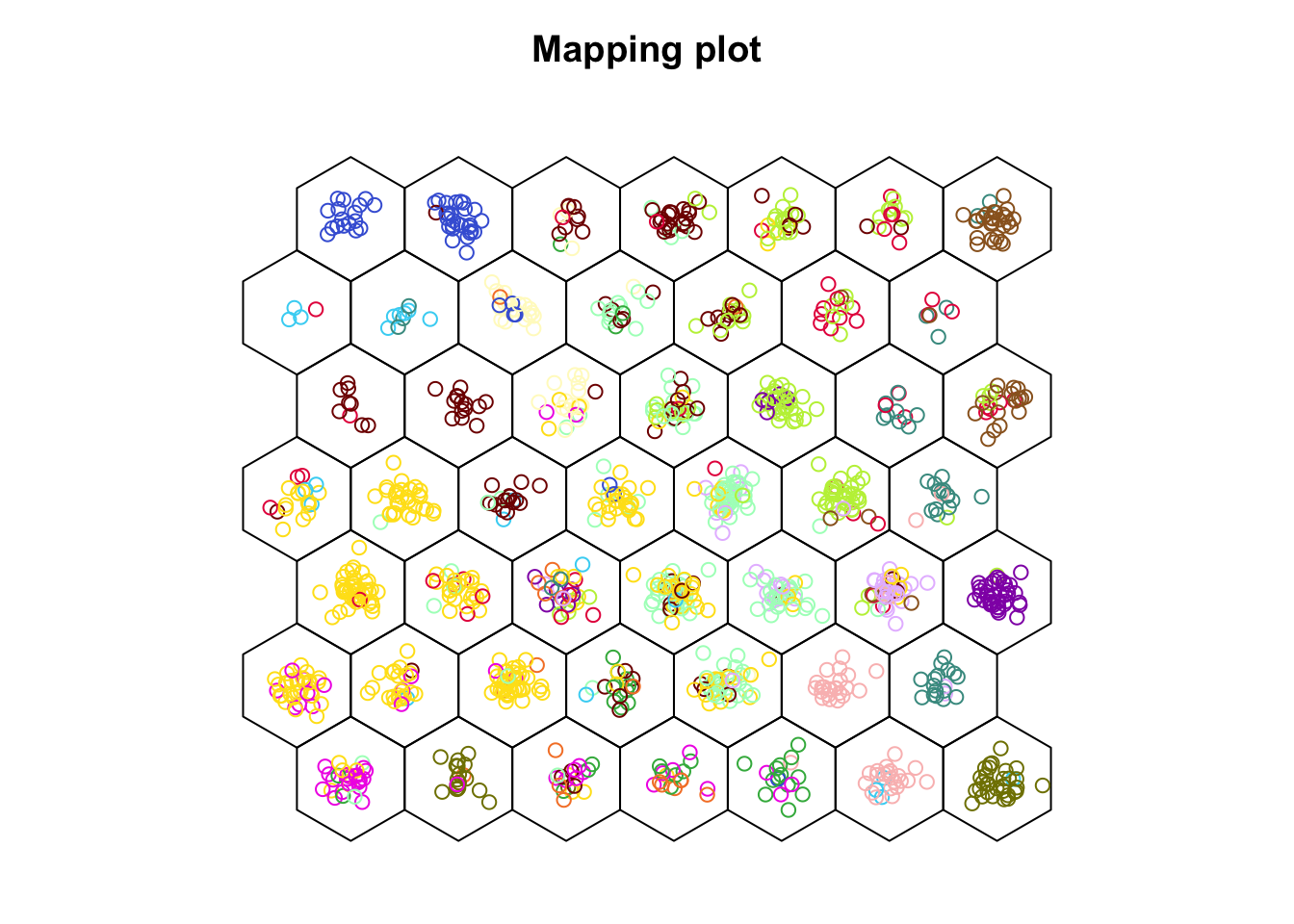
Nous n’avons pas ajouté de légende qui indique à quelle classe correspond quelle couleur. Ce que nous voulons voir, c’est si les cellules arrivent à séparer les classes. Nous voyons que la séparation est imparfaite, mais des tendances apparaissent avec certaines couleurs qui se retrouvent plutôt dans une région de la carte.
Nous voyons donc ici que, malgré que l’information contenue dans class n’ait pas été utilisées. Les différents individus de zooplancton ne se répartissent pas au hasard en fonction de ce critère. Nous pouvons également observer les cellules qui contiennent plus ou moins d’individus, mais si l’objectif est de visionner uniquement le remplissage des cellules, le type = "counts" est plus adapté.
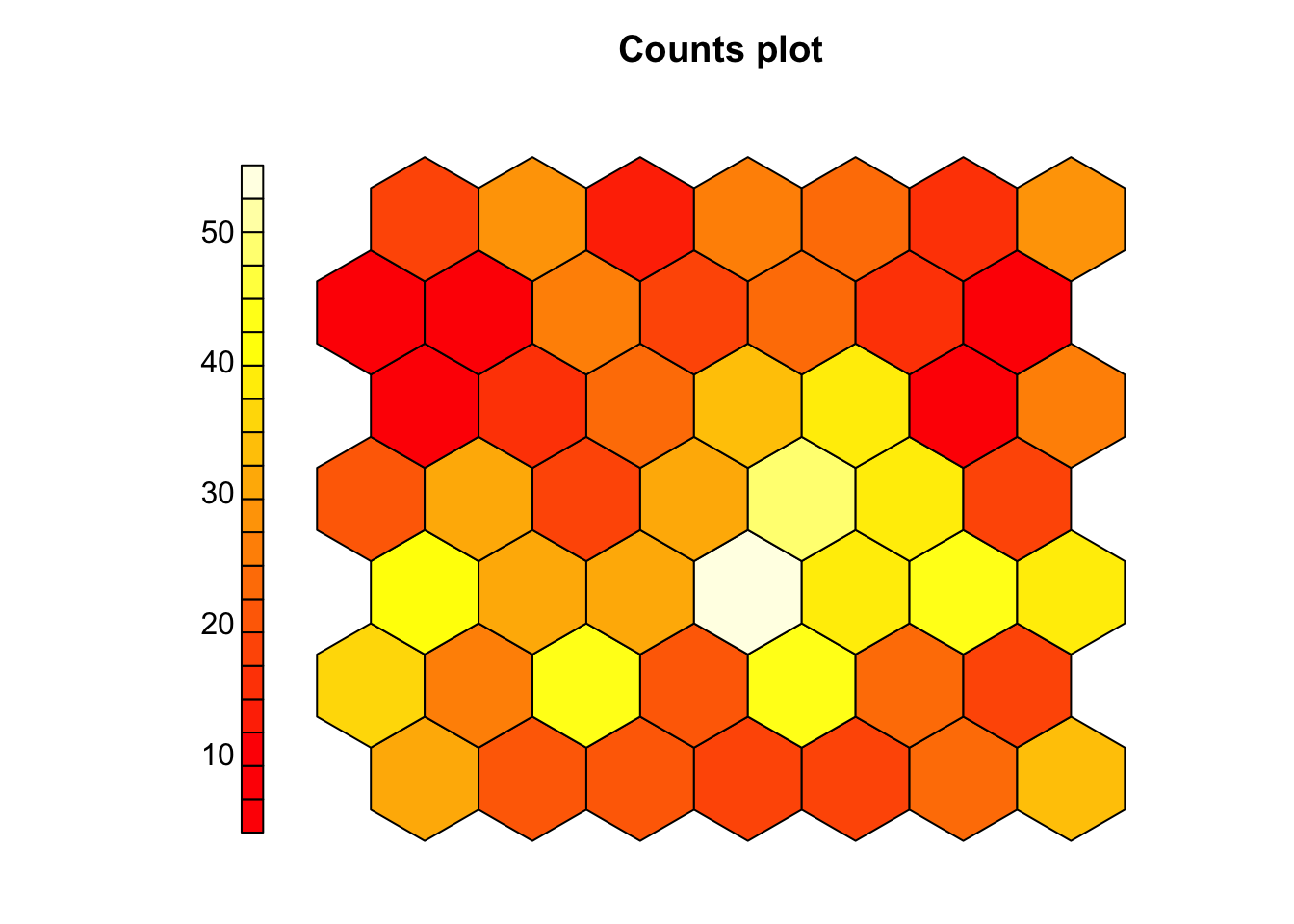
Nous pouvons obtenir la cellule dans laquelle chaque individu est mappé comme suit :
# [1] 32 28 20 39 12 32 23 26 23 32 37 15 28 16 39 48 25 5 23 4 47 25 47 46
# [25] 10 40 32 15 32 35 26 14 32 32 1 46 3 18 2 20 12 35 18 19 26 40 12 26
# [49] 41 33 27 7 19 26 41 19 20 8 19 26 15 14 32 16 28 8 16 35 16 19 28 14
# [73] 13 31 34 48 48 28 26 16 32 34 28 17 42 23 13 41 9 19 42 8 42 36 35 20
# [97] 20 19 20 7 20 26 20 20 2 20 19 2 17 13 17 14 27 27 20 18 12 20 20 20
# [121] 7 7 20 19 35 19 26 26 10 20 26 26 20 14 20 19 26 27 33 20 7 2 42 49
# [145] 22 37 29 23 25 28 14 17 34 16 40 45 15 9 40 22 17 39 7 18 34 49 33 1
# [169] 32 41 18 18 26 26 32 17 2 18 2 18 27 27 19 40 19 27 27 20 33 27 27 32
# [193] 4 27 18 2 48 39 48 33 48 33 17 47 34 15 18 20 32 27 33 20 12 32 27 16
# [217] 46 18 28 2 42 41 48 33 20 7 27 33 41 33 7 49 18 18 18 17 18 18 27 21
# [241] 18 19 7 10 18 7 7 18 27 18 17 2 7 18 27 27 2 7 18 7 2 18 18 7
# [265] 35 32 18 18 30 30 29 46 46 29 17 9 24 47 15 46 40 45 40 26 30 27 33 29
# [289] 45 30 15 24 47 40 32 20 16 16 30 17 16 40 24 9 46 2 45 16 29 46 16 15
# [313] 22 41 24 30 29 32 30 45 10 10 12 17 10 2 26 16 7 4 7 27 27 16 17 31
# [337] 32 11 17 16 2 41 26 2 33 26 15 10 10 17 3 2 40 20 10 11 33 27 40 33
# [361] 32 32 18 27 33 10 28 24 41 46 33 27 33 46 46 33 27 18 46 32 27 45 8 40
# [385] 35 46 32 48 46 46 46 35 4 27 40 46 33 15 46 33 28 18 33 20 20 27 27 10
# [409] 27 33 27 10 1 33 33 27 40 35 47 25 9 1 16 31 49 9 15 33 17 17 9 15
# [433] 37 26 32 12 21 22 20 47 23 24 45 5 15 6 11 21 1 46 24 42 37 15 19 15
# [457] 5 11 15 49 21 33 18 21 10 21 26 3 21 21 33 3 10 19 15 5 12 35 15 21
# [481] 19 19 19 18 12 21 21 5 17 15 10 8 12 38 21 38 19 1 15 10 21 4 12 21
# [505] 18 4 33 19 43 43 39 43 23 44 28 8 3 21 43 47 8 44 44 47 33 6 8 21
# [529] 8 8 36 12 38 19 21 35 1 20 4 20 6 40 1 19 12 48 44 31 21 41 44 37
# [553] 9 5 32 44 45 44 21 17 40 25 8 39 36 19 5 17 19 49 6 3 18 5 3 7
# [577] 3 12 21 45 8 8 3 23 4 22 1 1 8 37 24 43 1 26 34 38 44 36 21 21
# [601] 12 12 21 19 12 12 26 38 12 31 1 12 21 12 21 21 21 21 31 21 26 21 26 12
# [625] 31 43 38 15 21 38 8 25 24 31 13 11 15 37 5 5 13 10 38 38 43 45 38 1
# [649] 14 11 10 7 2 13 12 26 26 26 38 16 15 38 38 11 21 31 11 25 47 3 11 5
# [673] 15 38 5 48 18 26 22 44 31 21 21 21 5 39 18 1 21 21 12 11 17 21 9 4
# [697] 11 4 4 3 21 30 20 11 30 45 26 39 13 6 24 29 23 16 14 14 30 24 39 30
# [721] 24 9 24 29 47 13 24 30 13 15 14 25 30 45 6 29 40 30 24 24 31 6 24 14
# [745] 8 11 30 15 1 26 17 16 3 1 39 13 13 26 13 12 9 11 3 17 26 6 26 9
# [769] 38 38 32 11 18 49 15 32 13 13 1 37 39 23 13 3 6 39 14 44 6 25 1 6
# [793] 14 44 6 6 48 39 39 26 38 6 1 23 8 49 49 9 16 22 25 9 49 37 15 23
# [817] 15 13 26 12 10 49 20 19 19 26 12 18 19 13 10 12 1 15 12 19 12 10 18 2
# [841] 10 49 4 13 18 13 26 26 26 26 9 15 25 32 16 44 44 8 32 40 18 46 32 26
# [865] 8 44 9 23 46 11 8 25 8 40 25 23 32 8 25 15 16 15 47 15 10 11 18 18
# [889] 10 18 46 26 10 15 17 15 4 40 41 3 10 18 10 18 10 19 10 10 41 9 19 12
# [913] 10 17 49 15 18 31 47 8 44 48 40 15 44 40 32 10 23 48 8 23 22 25 44 15
# [937] 38 25 44 22 9 16 16 19 8 5 9 1 9 15 22 16 16 20 10 49 12 18 41 12
# [961] 18 1 5 18 3 18 19 12 10 10 10 23 25 22 47 32 18 5 3 48 38 23 28 47
# [985] 39 8 31 39 8 31 25 22 47 16 39 31 8 1 15 25 25 43 23 11 22 23 22 18
# [1009] 23 12 35 18 18 1 8 41 1 12 8 44 19 47 8 44 10 43 15 25 44 1 47 32
# [1033] 12 43 1 25 23 8 8 23 8 25 1 22 26 16 44 22 34 25 16 49 12 17 1 26
# [1057] 42 5 12 11 12 12 20 4 10 10 10 38 23 43 23 23 44 39 44 43 8 47 38 22
# [1081] 38 23 43 46 22 43 47 47 48 35 40 22 25 43 38 47 23 23 25 47 18 44 44 25
# [1105] 34 22 43 23 44 44 43 32 25 17 23 35 46 6 27 41 19 26 16 20 12 49 31 27
# [1129] 9 46 20 49 31 25 33 34 27 33 41 9 38 33 9 24 47 31 31 35 27 49 33 31
# [1153] 49 35 35 49 49 33 33 33 33 49 12 33 35 35 19 38 8 25 9 45 35 5 4 4
# [1177] 49 3 28 4 35 35 49 35 4 27 39 35 49 27 49 49 49 49 10 14 6 34 13 6
# [1201] 31 28 14 11 13 6 14 20 6 6 17 13 17 46 20 28 31 14 34 6 7 14 7 17
# [1225] 7 27 19 26 35 6 6 20 13 6 7 7 20 7 7 7 7 12 2 26 20 7 7 7
# [1249] 20 20 7 2 7 17 28 3 28 3 10 1 9 10Par conséquent, nous pouvons créer un tableau de contingence qui répertorie le nombre d’individus mappés dans chaque cellule à l’aide de table(). Nous l’enregistrons dans zoo_som_nb car nous la réutiliserons plus tard.
#
# 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
# 30 20 20 18 18 24 33 36 25 43 20 44 23 18 42 30 31 55 38 43 39 20 31 18 30 48
# 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49
# 39 17 9 15 22 34 38 11 25 4 9 25 19 23 16 7 17 28 13 26 24 15 296.3.2 Interprétation d’un SOM
De nombreuses autres présentations graphiques sont possibles sur cette base. Nous allons explorer deux aspects complémentaires : (1) représentation des variables, et (2) réalisation et représentation de regroupements.
6.3.2.1 Représentation des variables
La carte SOM est orientée. C’est-à-dire que les cellules représentent des formes différentes de plancton telles qu’exprimées à travers les 19 variables utilisées ici (quantification de la taille, de la forme, de la transparence, …). Le graphique type = "codes" permet de visualiser ces différences de manière générale :

Ce graphique est riche en informations. Nous voyons que :
- les très grands individus (
ecd,area,perimeter, etc.), soit les segments verts sont en haut à gauche de la carte et les petits sont à droite, - les individus opaques (variables
mean,mode,max, etc.18), soit des segments dans les tons jaunes sont en haut à droite. Les organismes plus transparents sont en bas à gauche, - au delà de ces deux principaux critères qui se dégagement prioritairement, les aspects de forme (segments rose-rouges) se retrouvent exprimés moins nettement le long de gradients. La
circularitymesure la silhouette plus ou moins arrondie des items (sa valeur est d’autant plus élevée que la forme se rapproche d’un cercle). Les organismes circulaires se retrouvent dans le haut de la carte. L’elongationet l’aspectmesurent l’allongement de la particule et se retrouvent plutôt exprimés positivement dans le bas de la carte.
Nous pouvons donc orienter notre carte SOM en indiquant l’information relative aux variables. Lorsque le nombre de variables est élevé ou relativement élevé comme ici, cela devient néanmoins difficile à lire. Il est aussi possible de colorer les cartes en fonction d’une et une seule variable pour en faciliter la lecture à l’aide de type = "property". Voici quelques exemples (notez la façon de diviser une page graphique en lignes et colonnes à l’aide de par(mfrow = )) en graphiques R de base, ensuite une boucle for réalise les six graphiques l’un après l’autre) :
par(mfrow = c(2, 3))
for (var in c("size", "mode", "range", "aspect", "elongation", "circularity"))
plot(zoo_som, type = "property", property = zoo_som$codes[[1]][, var],
main = var, palette.name = viridis::inferno)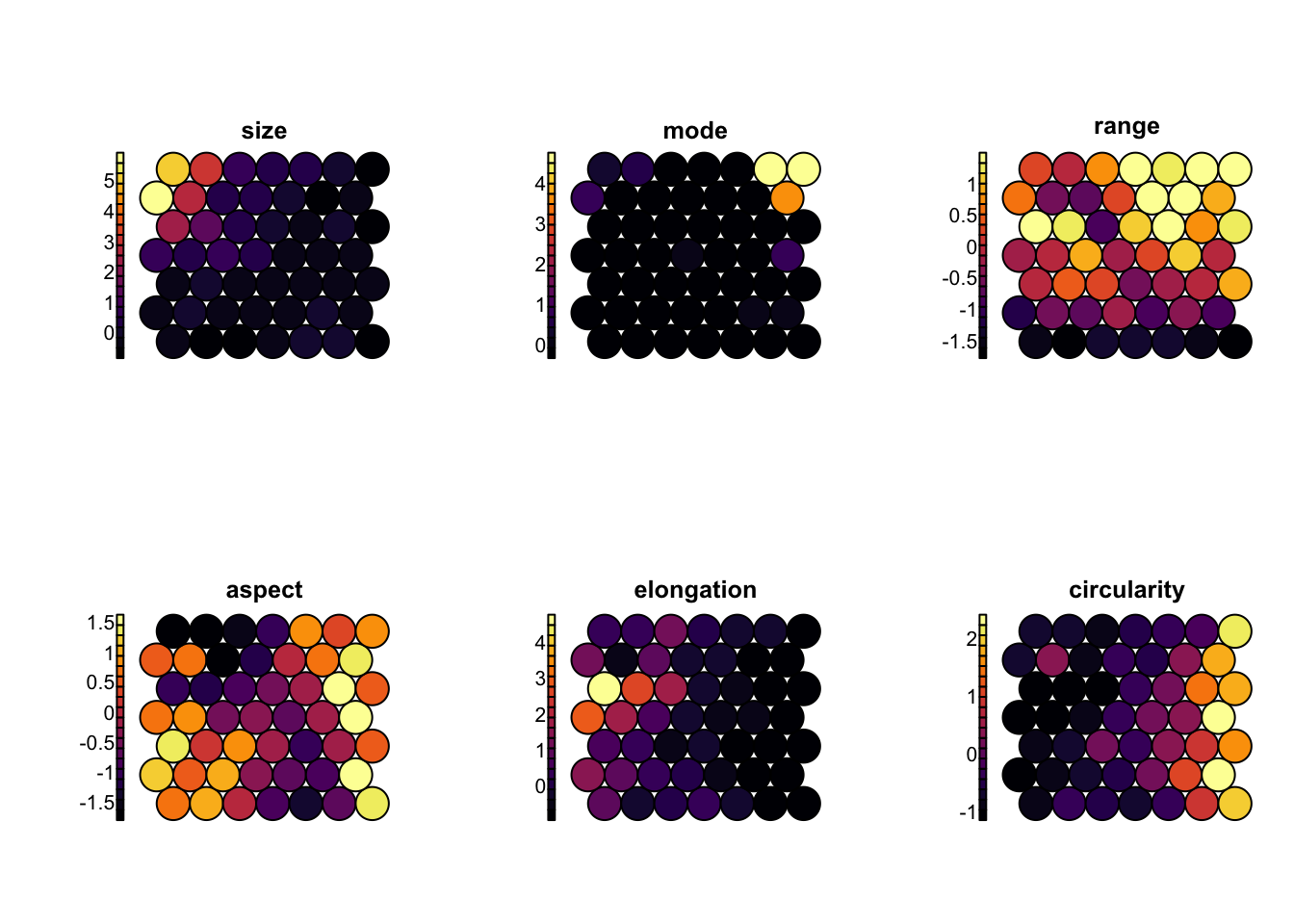
Nous pouvons plus facilement inspecter les zones d’influence de différentes variables ciblées. Ici, size est une mesure de la taille des particules, mode est le niveau d’opacité moyen, range est la variation d’opacité (un range important indique que la particule a des parties très transparentes et d’autres très opaques), aspect est le rapport longueur/largeur, elongation est une indication de la complexité du périmètre de la particule, et circularity est sa forme plus ou moins circulaire. Pour une explication détaillée des 19 variables, faites ?zooplankton.
6.3.2.2 Regroupements
Lorsque nous avons réalisé une CAH sur le jeu de données zooplankton, nous étions obligés de choisir deux variables parmi les 19 pour visualiser le regroupement sur un graphique nuage de points. C’est peu, et cela ne permet pas d’avoir une vision synthétique sur l’ensemble de l’information. Les méthodes d’ordination permettent de visualiser plus d’information sur un petit nombre de dimensions grâce aux techniques de réduction des dimensions qu’elles implémentent. Les cartes SOM offrent encore un niveau supplémentaire de raffinement. Nous pouvons considérer que chaque cellule est un premier résumé des données et nous pouvons effectuer ensuite une CAH sur ces cellules afin de dégager un regroupement et le visualiser sur la carte SOM. L’intérêt est que l’on réduit un jeu de données potentiellement très volumineux à un nombre plus restreint de cellules (ici 7x7 = 49), ce qui est plus “digeste” pour la CAH. Voici comment ça fonctionne (notez que dissimilarity() attend un data frame alors que som() travaille avec des objets matrix, donc une conversion s’impose ici) :
# Distance euclidienne entre cellules
zoo_som_dist <- dissimilarity(as.data.frame(zoo_som$codes[[1]]),
method = "euclidean")
zoo_som_cah <- cluster(zoo_som_dist, method = "ward.D2", members = zoo_som_nb)Notre CAH a été réalisée ici avec la méthode D2 de Ward. L’argument members = est important. Il permet de pondérer chaque cellule en fonction du nombre d’individus qui y sont mappés. Toutes les cellules n’ont pas un même nombre d’individus, et nous souhaitons mettre plus de poids dans l’analyse aux cellules les plus remplies.
Voici le dendrogramme :
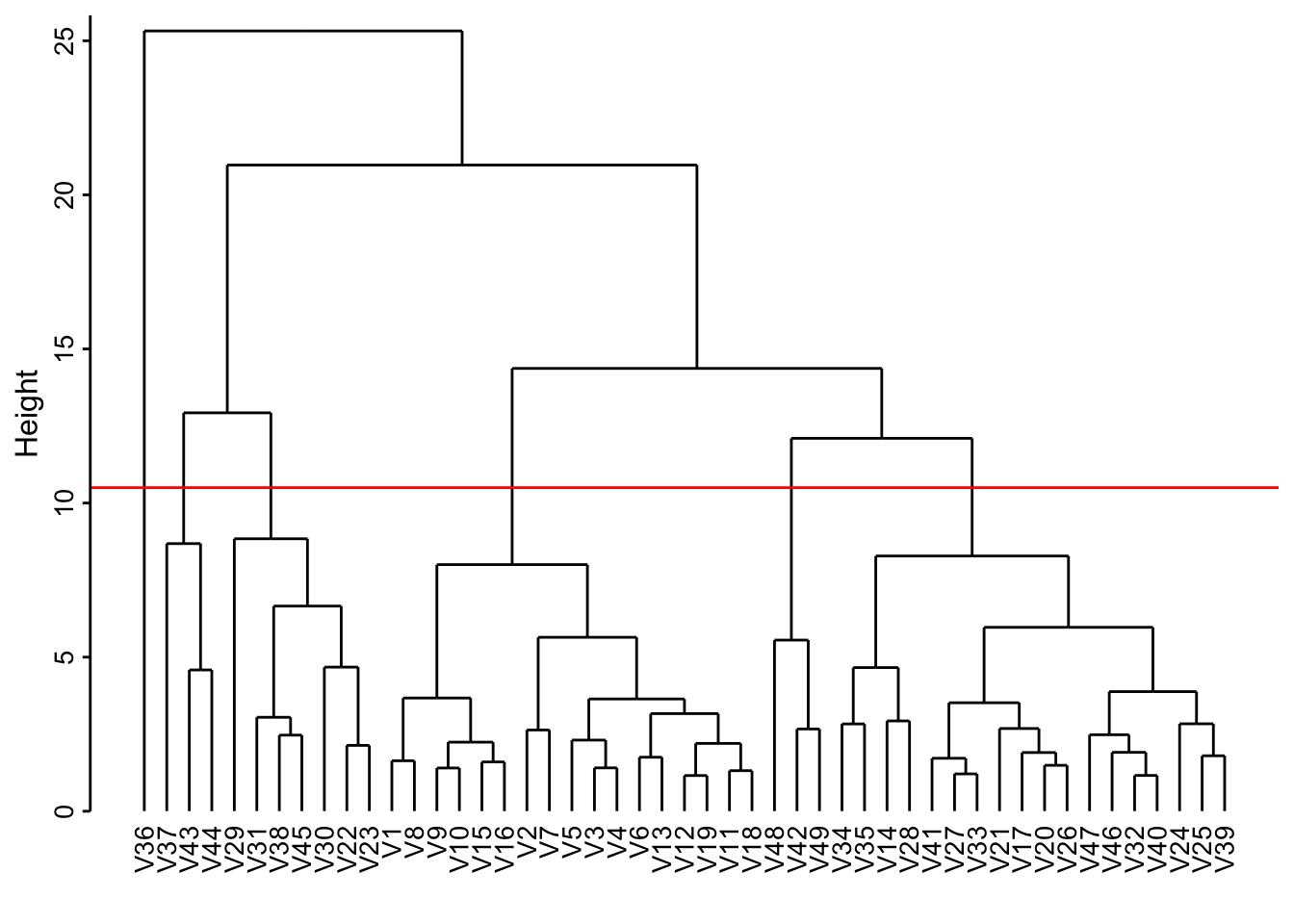
Les V1 à V49 sont les numéros de cellules. Nous pouvons couper à différents endroits dans ce dendrogramme, mais si nous décidons de distinguer les six groupes correspondants au niveau de coupure à une hauteur de 10,5 (comme sur le graphique), voici ce que cela donne :
# V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15 V16 V17 V18 V19 V20
# 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 2 1 1 2
# V21 V22 V23 V24 V25 V26 V27 V28 V29 V30 V31 V32 V33 V34 V35 V36 V37 V38 V39 V40
# 2 3 3 2 2 2 2 2 3 3 3 2 2 2 2 4 5 3 2 2
# V41 V42 V43 V44 V45 V46 V47 V48 V49
# 2 6 5 5 3 2 2 6 6Visualisons ce découpage sur la carte SOM (l’argument bgcol = colorie le fond des cellules en fonction des groupes19, et add.cluster.boudaries() individualise des zones sur la carte en fonction du regroupement choisi).
plot(zoo_som, type = "mapping", pch = ".", main = "SOM zoo, six groupes",
bgcol = RColorBrewer::brewer.pal(5, "Set2")[groupes])
add.cluster.boundaries(zoo_som, clustering = groupes)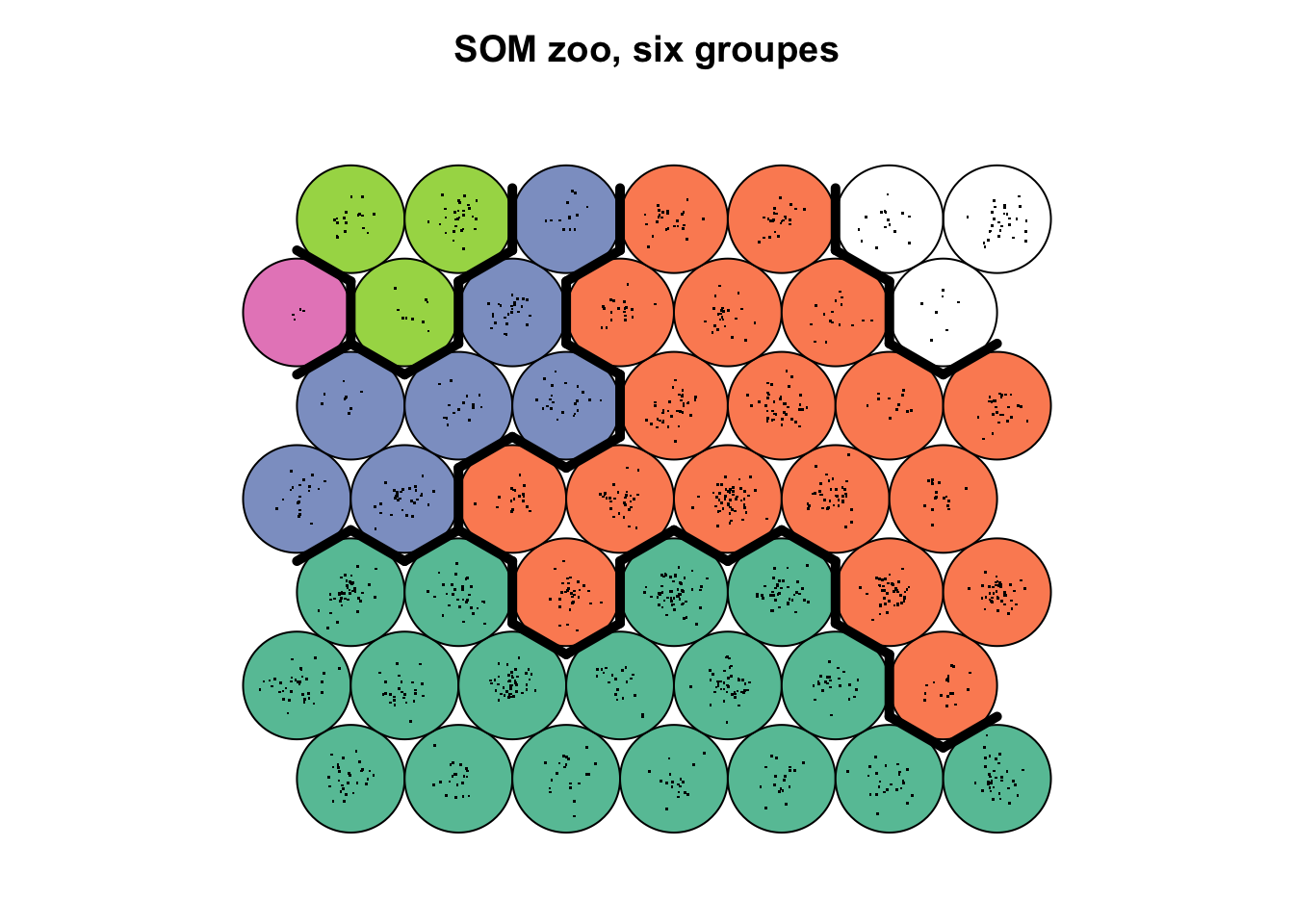
Grâce à la topographie des variables que nous avons réalisée plus haut, nous savons que :
- le groupe vert bouteille en bas reprend les petites particules plutôt transparentes,
- le groupe orange à droite est constitué de particules très contrastées avec des parties opaques et d’autres transparentes (
rangedans les niveaux de gris important) mais globalement foncées (modecorrespondant au niveau de gris le plus représenté faible), - le groupe du dessus à droite en blanc est constitué d’autres particules très contrastées, mais à dominante claire (
modeélevé), - le groupe bleu est constitué des particules moyennes à grandes ayant une forme complexe (variable
elongationélevée), - les groupes vert clair et rose en haut à gauche reprend les toutes grandes particules, avec la cellule unique en rose qui reprend les plus grosses.
Nous n’avons fait qu’effleurer les nombreuses possibilités des cartes auto-adaptatives SOM… Il est par exemple possible d’aller mapper des nouveaux individus dans cette carte (données supplémentaires), ou même de faire une classification sur base d’exemples (classification supervisée) que nous verrons au cours de Science des Données Biologiques III. Nous espérons que cela vous donnera l’envie et la curiosité de tester cette méthode sur vos données et d’explorer plus avant ses nombreuses possibilités.
Pour en savoir plus
Une explication très détaillée en français accompagnée de la résolution d’un exemple fictif dans R.
Une autre explication détaillée en français avec exemple dans R.
Si vous êtes aventureux, vous pouvez vous lancer dans la réimplémentation des graphiques du package {kohonen} en {chart} ou {ggplot2}. Voici un bon point de départ (en anglais).
À vous de jouer !
Effectuez maintenant les exercices du tutoriel B06Lc_som (Ordination et regroupement grâce aux cartes auto-adaptatives).
BioDataScience2::run("B06Lc_som")Réalisez le travail B06Ia_fish_market, partie III.
Travail individuel pour les étudiants inscrits au cours de Science des Données Biologiques II à l’UMONS (Q2 : analyse) à terminer avant le 2022-03-07 23:59:59.
Initiez votre projet GitHub Classroom
Voyez les explications dans le fichier README.md, partie III.