5.1 Rendement photosynthétique

Afin d’avoir un premier aperçu de ce qu’est une régression non linéaire par les moindres carrés et comment on la calcule dans R, nous allons détailler un exemple concret. La posidonie Posidonia oceanica (L.) Delile (1813) est une plante à fleurs marine qui forme des herbiers denses en mer Méditerranée. Ses feuilles sont particulièrement adaptées à l’utilisation de la lumière qui règne à quelques mètres en dessous de la surface où elle prospère en herbiers denses.

Herbier de posidonies par Frédéric Ducarme, wikimedia, license Creative Commons Attribution-Share Alike 4.0.

Pour étudier le rendement de sa photosynthèse, c’est-à-dire la part du rayonnement lumineux reçu qui est effectivement utilisée pour initier la chaîne de transport d’électrons au sein de son photosystème II, nous pouvons utiliser un appareil spécialisé : le diving PAM.

Diving PAM, photo par Arnaud Abadie.

Cet appareil est capable de déterminer le taux de transfert des électrons (ETR en µmol électrons/m²/s) par l’analyse de la fluorescence réémise par la plante lorsque ses photosites sont excités par une lumière monochromatique pulsée (Walz 2018). Une façon de déterminer la réponse de la plante en rendement photosynthétique en fonction de l’intensité de la lumière reçue est de mesurer successivement l’ETR pour différentes intensités de lumière. En anglais cela s’appelle la “Rapid Light Curve” ou RLC en abrégé. Comme toutes les longueurs d’ondes lumineuses ne sont pas utilisables par la chlorophylle, l’intensité lumineuse est exprimée dans une unité particulière, le “PAR” ou “Photosynthetically Active Radiation” en µmol photons/m²/s. Une RLC représente donc la variation de l’ERT en fonction des PAR⁸. Une RLC typique commence par une relation quasi linéaire aux faibles intensités, pour s’infléchir et atteindre un plateau de rendement maximum. Au delà, si l’intensité lumineuse augmente encore, des phénomènes de photoinhibition apparaissent et le rendement diminue dans une troisième phase. Voici une RLC mesurée à l’aide du diving PAM sur une feuille de P. oceanica.

rlc <- as_dtx(tribble(
  ~etr, ~par,
  0.0,  0,
  0.5,  2,
  3.2,  11,
  5.7,  27,
  7.4,  50,
  8.4,  84,
  8.9,  170,
  8.4,  265,
  7.8,  399
))
rlc <- labelise(rlc, self = FALSE,
  label = list(etr = "ETR", par = "PAR"),
  units = list(etr = "µmol électrons/m^2/s", par = "µmol photons/m^2/s")
)
chart(data = rlc, etr ~ par) +
  geom_point()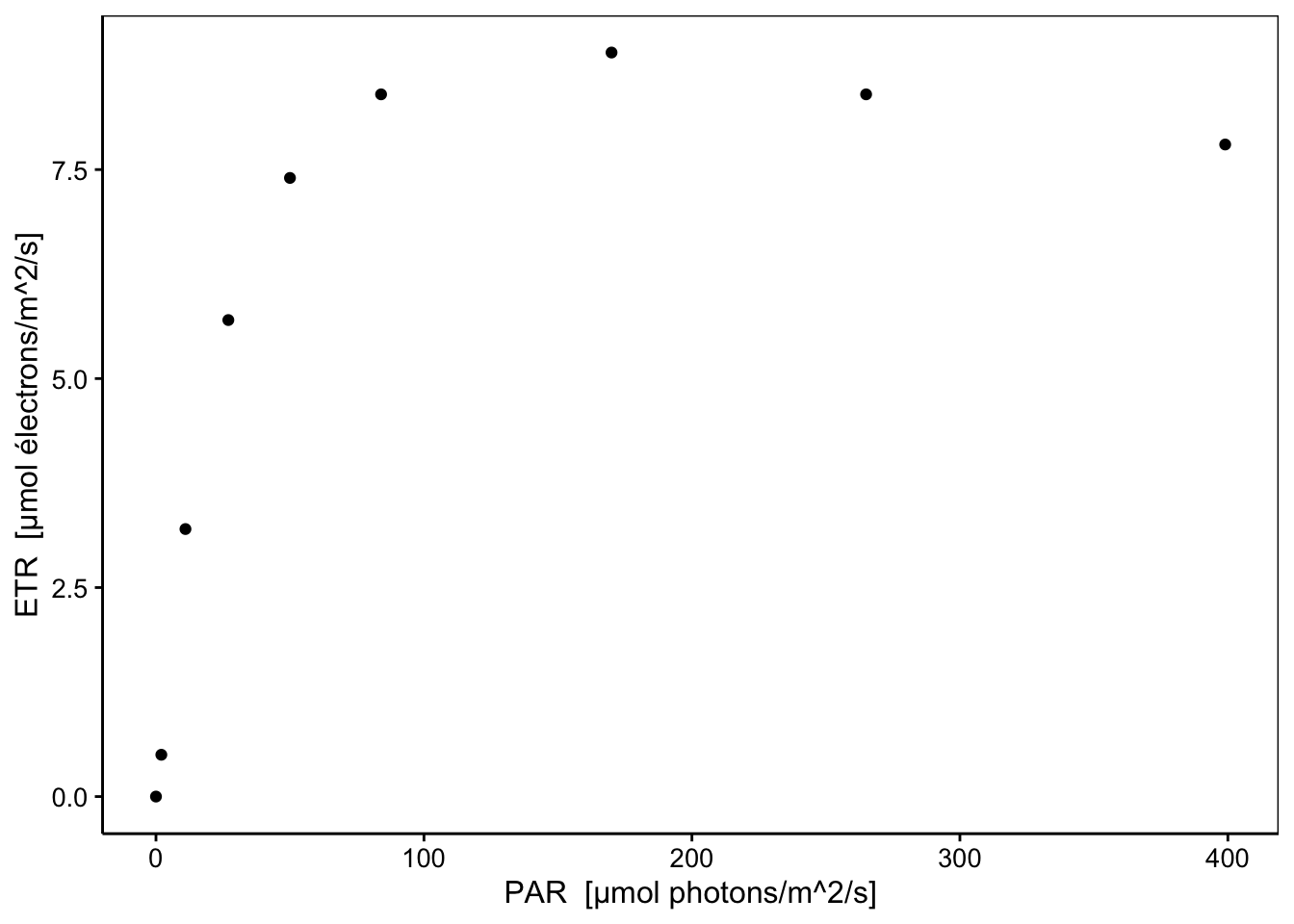

Les trois phases successives sont bien visibles ici (linéaire pour des PAR de 0 à 25, plateau à des PAR de 150-200 et photoinhibition à partir de 200 PAR). Naturellement, une régression linéaire dans ces données n’a pas de sens. Une régression polynomiale d’ordre trois donnerait ceci :

rlc_lm <- lm(data = rlc, etr ~  par + I(par^2) + I(par^3))
chart(rlc_lm)

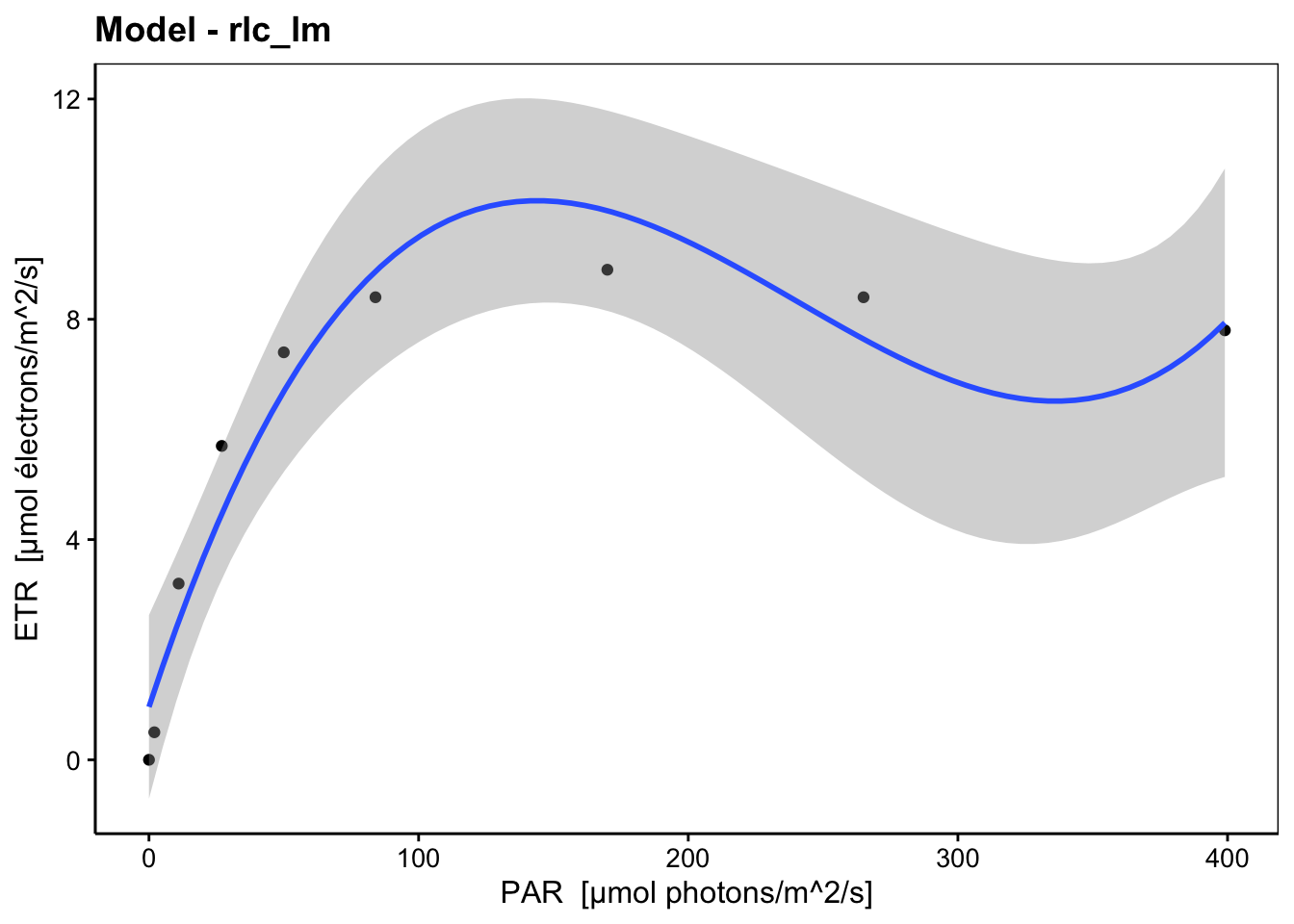
La régression polynomiale tente maladroitement de s’ajuster dans les données, mais est incapable de retranscrire les trois phases correctement. En particulier, la troisième est incorrecte puisque le modèle semble indiquer une reprise du rendement aux intensités les plus élevées. Une représentation incorrecte est à craindre lorsque le modèle mathématique utilisé ne représente pas les différentes caractéristiques du phénomène étudié. L’utilisation d’un modèle adéquat est possible ici seulement par régression non linéaire. En effet, aucune transformation monotone croissante ou décroissante ne peut linéariser ce type de données puisque la courbe monte d’abord pour s’infléchir ensuite.

Quand passer à la régression non linéaire ?

Nous pouvons être amenés à utiliser une régression non linéaire pour l’une de ces deux raisons, voire les deux en même temps :

• Lorsque le nuage de points est curvilinéaire, évidemment, mais après avoir tenté de le linéariser (et de résoudre un problème éventuel d’hétéroscédasticité ou de non-normalité des résidus) par transformation sans succès,

• En fonction de nos connaissances a priori du phénomène. Tout phénomène issu d’un mécanisme dont nous connaissons le mode de fonctionnement menant à une équation mathématique non linéaire. Cela se rencontre fréquemment en physique, en chimie, et même en biologie (courbes de croissance, effet de modifications environnementales, etc.)

Les spécialistes de la photosynthèse ont mis au point différents modèles pour représenter les RLC. (Platt, Gallegos, and Harrison 1980) ont proposé une formulation mathématique des phénomènes mis en jeu ici. Leur équation est la suivante :

\[ETR = ETR_{max} \cdot (1 - e^{-PAR \cdot \alpha/ETR_{max}}) \cdot e^{-PAR \cdot \beta/ETR_{max}}\]

avec \(PAR\) la variable indépendante, \(ETR\), la variable dépendante, et \(ETR_{max}\), \(\alpha\) et \(\beta\), les trois paramètres du modèle. \(ETR_{max}\) est le rendement maximum possible, \(\alpha\) est la pente de la partie initiale linéaire avant infléchissement vers le maximum et \(\beta\) est le coefficient de photoinhibition.

En matière de régression non linéaire, il est tout aussi important de bien comprendre les propriétés mathématiques de la fonction utilisée que de faire un choix judicieux du modèle. En particulier, il faut s’attacher à bien comprendre la signification (biologique) des paramètres du modèle. Non seulement, cela aide à en définir des valeurs initiales plausibles, mais c’est aussi indispensable pour pouvoir ensuite bien interpréter les résultats obtenus.

Nous pouvons facilement créer une fonction dans R qui représente ce modèle :

pgh_model <- function(x, etr_max, alpha, beta)
  etr_max * (1 - exp(-x * alpha/etr_max)) * (exp(-x * beta/etr_max))

Le premier argument de la fonction doit être la variable indépendante (notée de manière générique x, mais n’importe quel nom fait l’affaire ici) et les autres arguments correspondent aux paramètres du modèle, donc etr_max, alpha et beta. Ce modèle peut être ajusté dans R à l’aide de la fonction nls() pour “Nonlinear Least Squares” (regression). Par contre, nous devons fournir une information supplémentaire (l’explication sera détaillée plus loin) : des valeurs approximatives de départ pour les paramètres. Nous voyons sur le graphique que etr_max = 9 est une estimation plausible, mais il est difficile de déterminer alpha et beta rien qu’en regardant le graphique. Nous allons fixer alpha = 1 (rendement max), et partir d’un modèle sans photoinhibition en utilisant beta = 0. Voici comment la régression non linéaire par les moindres carrés avec notre fonction pgh_model peut être calculée :

rlc_nls <- nls(data = rlc, etr ~ pgh_model(par, etr_max, alpha, beta),
  start = list(etr_max = 9, alpha = 1, beta = 0))
summary(rlc_nls)

# 
# Formula: etr ~ pgh_model(par, etr_max, alpha, beta)
# 
# Parameters:
#         Estimate Std. Error t value Pr(>|t|)    
# etr_max 9.351065   0.261969  35.695 3.22e-08 ***
# alpha   0.327385   0.013416  24.402 3.11e-07 ***
# beta    0.003981   0.001084   3.673   0.0104 *  
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 
# Residual standard error: 0.1729 on 6 degrees of freedom
# 
# Number of iterations to convergence: 7 
# Achieved convergence tolerance: 3.827e-06

La dernière ligne, “achieved convergence” indique que le modèle a pu être calculé. Nous avons un tableau des paramètres qui ressemble très fort à celui de la régression linéaire, y compris les tests t de Student sur chacun des paramètres. Nous obtenons etr_max = 9.4, alpha = 0.33 et beta = 0.0040, mais d’après le test de Student ce dernier paramètre n’est pas significativement différent de zéro⁹. Pour l’instant, nous allons conserver ce modèle tel quel. Notre modèle paramétré donne donc :

\[ETR = 9.4 \cdot (1 - e^{-PAR \cdot 0.33/9.4}) \cdot e^{-PAR \cdot 0.0040/9.4}\]

Voyons ce que cela donne sur le graphique. Nous utiliserons pour ce faire une petite astuce qui consiste à transformer l’objet nls obtenu en une fonction utilisable par stat_function() pour le graphique ggplot2 réalisé à l’aide de chart()¹⁰.

as.function.nls <- function(x, ...) {
  nls_model <- x
  name_x <- names(nls_model$dataClasses)
  stopifnot(length(name_x) == 1)
  function(x) predict(nls_model, newdata = structure(list(x), names = name_x))
}

Maintenant, nous allons pouvoir ajouter la courbe correspondant à notre modèle comme ceci :

chart(data = rlc, etr ~ par) +
  geom_point() +
  stat_function(fun = as.function(rlc_nls))

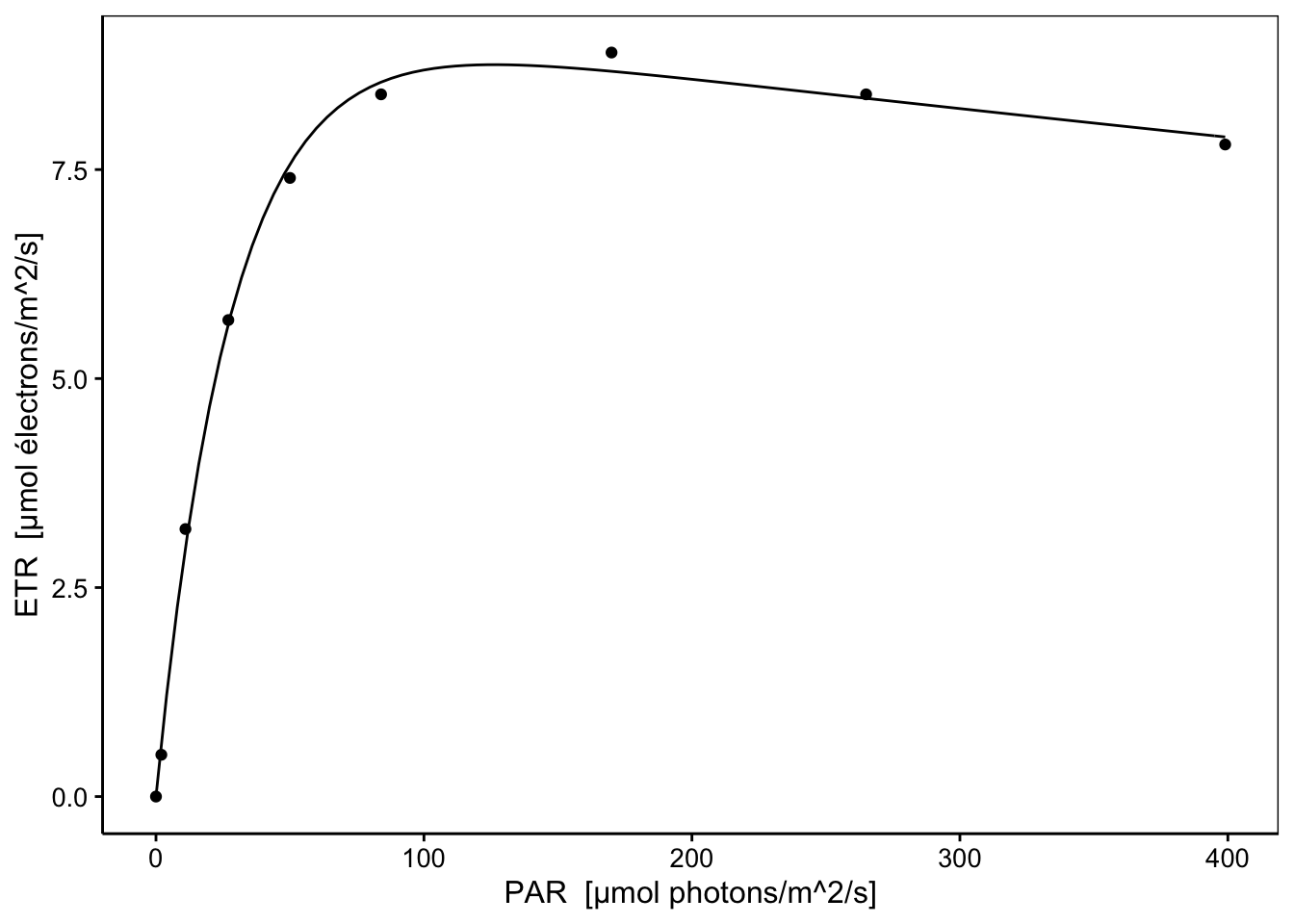
Ce modèle représente bien mieux le phénomène étudié, et il s’ajuste d’ailleurs beaucoup mieux également dans les données que notre polynôme. Une comparaison sur base du critère d’Akaike est également en faveur de ce dernier modèle non linéaire (pour rappel, plus la valeur est faible, mieux c’est) :

AIC(rlc_lm, rlc_nls)

# # A data.frame: 2 x 2
#   ` `           df   AIC
#   <rownames> <dbl> <dbl>
# 1 rlc_lm         5 31.8 
# 2 rlc_nls        4 -1.70

Super ! Nous venons de réaliser ensemble notre première régression non linéaire par les moindres carrés. Étudions un petit peu plus dans le détail cette technique dans la section suivante. En effet, il est utile de connaitre et comprendre les différents pièges qui peuvent se présenter à nous pour les éviter.

À vous de jouer !

Références

Platt, T., C. L. Gallegos, and W. G. Harrison. 1980. “Photoinhibition of Photosynthesis in Natural Assemblages of Marine Phytoplankton.” Journal of Marine Research 38: 687–701.

Walz, Heinz. 2018. “Saturation Pulse Analysis.” In DIVING-PAM-II: Underwater Chlorophyll Fluorometer Manual, edited by Heinz Walz GmbH, 49:81–94. February. https://walz.com/downloads/manuals/diving-pam-II/DIVING_PAM_II_02.pdf.

---

8. Techniquement, l’ERT nécessite d’effectuer des mesures après stabilisation de la photosynthèse, ce qui prend plusieurs minutes. Donc, une courbe rapide est discutable de ce point de vue, mais reste un outil utile en écophysiologie où la comparaison de différentes RLCs indique un changement de capacité photosynthétique de la plante.↩︎

9. Il faut faire attention ici, cela peut aussi signifier que nous n’avons pas assez de points après le plateau pour pouvoir estimer correctement \(\beta\) !↩︎

10. Il est également possible de l’utiliser avec curve() pour un graphique de base dans R.↩︎