2.5 Modèle empirique et mécaniste

Un modèle empirique est issu de l’observation. Nous collectons des données et nous cherchons à les prédire via un modèle statistique. L’important ici est d’obtenir une bonne prédiction, c’est-à-dire, une erreur quadratique moyenne du modèle la plus faible possible. Cependant, la forme mathématique du modèle n’a, éventuellement, rien à voir avec le mécanisme qui génère les données. C’est typiquement le cas pour un modèle polynomial d’ordre élevé.

Outre les prédictions pour lesquelles ce modèle est taillé par construction, un modèle linéaire simple ou multiple peut s’avérer également utile pour révéler les relations qui existent entre les variables impliquées… tout en restant très prudent concernant la colinéarité qui peut faire penser que des variables fortement corrélées entre elles aient faussement un pouvoir explicatif.

Dans le cas de trees, nos différents essais suggèrent que le diamètre du tronc pourrait être une variable explicative lorsqu’elle est élevée au carré. La hauteur est également utile, sous forme non transformée.

Un modèle mécaniste vise à expliciter le mécanisme qui est responsable de la relation observée. De tels modèles sont plus courants en physique, voire en chime qu’en biologie, mais il y en a. Le modèle mécaniste est plus difficile à définir car il implique une compréhension profonde de ce qui se passe. Dans cas de trees, il ne faut pas être un génie pour se rendre compte que le tronc de l’arbre peut être assimilé, en première approximation, à un cône. Par conséquent, le volume de bois peut être approximé par la formule suivante :

\[volume = \frac{1}{3} . \pi . rayon^2 . hauteur\]

Avec notre diamètre au carré et notre hauteur, nous n’étions pas loin, à ceci près que les deux variables sont additionnées, et non multipliées dans notre modèle. La régression linéaire, et comme nous le verrons au chapitre suivant, le modèle linéaire sont fondamentalement des modèles additifs où les différents termes s’additionnent. Cependant, nous pouvons faire intervenir un terme qui multiplie nos deux variables explicatives par l’intermédiaire des interactions comme pour l’ANOVA à deux facteurs, voir section 11.3 de SDD I. Afin de nous rapprocher de la formule du volume d’un cône, calculons à présent le carré du rayon et ajustons un modèle linéaire multiple avec interactions :

trees <- smutate(trees, radius2 = (diameter/2)^2)
trees_lm7 <- lm(data = trees, volume ~ radius2 * height) # Forme compacte
# Forme développée, équivalente à la forme compacte
trees_lm7 <- lm(data = trees, volume ~ radius2 + height + radius2:height)
summary(trees_lm7)

# 
# Call:
# lm(formula = volume ~ radius2 + height + radius2:height, data = trees)
# 
# Residuals:
#       Min        1Q    Median        3Q       Max 
# -0.139754 -0.029324 -0.002796  0.049657  0.120782 
# 
# Coefficients:
#                Estimate Std. Error t value Pr(>|t|)  
# (Intercept)    -0.04178    0.33906  -0.123   0.9028  
# radius2        -1.25193   12.41304  -0.101   0.9204  
# height          0.00173    0.01453   0.119   0.9061  
# radius2:height  1.26682    0.50736   2.497   0.0189 *
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 
# Residual standard error: 0.07299 on 27 degrees of freedom
# Multiple R-squared:  0.9779,  Adjusted R-squared:  0.9754 
# F-statistic: 397.5 on 3 and 27 DF,  p-value: < 2.2e-16

Ce modèle est le suivant :

\[volume = a_1.radius^2 + a_2.height + a_3. radius^2.height + b + \epsilon\]

Or, le résumé du modèle nous indique clairement que \(a_1\), \(a_2\) et \(b\) sont tous les trois non significativement différents de zéro. Nous pouvons donc simplifier notre modèle à :

\[volume = a_3 . radius^2.height + \epsilon\]

… qui est mathématiquement équivalent à la formule qui calcule le volume d’un cône. Cela donne :

trees_lm8 <- lm(data = trees, volume ~ radius2:height + 0)
summary(trees_lm8)

# 
# Call:
# lm(formula = volume ~ radius2:height + 0, data = trees)
# 
# Residuals:
#       Min        1Q    Median        3Q       Max 
# -0.132684 -0.029572 -0.009963  0.045788  0.123879 
# 
# Coefficients:
#                Estimate Std. Error t value Pr(>|t|)    
# radius2:height  1.21433    0.01569    77.4   <2e-16 ***
# ---
# Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# 
# Residual standard error: 0.06956 on 30 degrees of freedom
# Multiple R-squared:  0.995,   Adjusted R-squared:  0.9949 
# F-statistic:  5990 on 1 and 30 DF,  p-value: < 2.2e-16

AIC(trees_lm8)

# [1] -74.31119

rmse(trees_lm8, trees)

# [1] 0.06842465

Avec ce dernier modèle, nous avons une équation très simple pour laquelle un seul paramètre doit être évalué. L’estimateur de ce paramètre vaut 1,21. Il n’est pas très éloigné de la valeur théorique \(1/3 . \pi = 1.05\). Souvenons-nous que le tronc de nos cerisiers noirs a une forme plus complexe qu’un cône et que le diamètre est mesuré à 4 pieds 6 pouces = 1,37m au dessus du sol (voir ?trees) alors que la formule du cône utilise le rayon à la base du cône, sachant que le bûcheron coupe son arbre quand même plus bas que cela.

Avec ce modèle, nous obtenons le critère d’Akaiké et l’erreur quadratique moyenne les plus faibles aussi. Tout indique que c’est le meilleur modèle, et en plus, il est mécaniste en ce sens qu’il fait intervenir la géométrie pour expliquer un volume à partir de deux dimensions dont l’une est élevée au carré. D’ailleurs, une analyse dimensionnelle (comparaison des unités intervenant à gauche et à droite dans l’équation) montre aussi qu’il est cohérent de ce point de vue : un volume en m³ s’obtient bien par la multiplication d’une dimension en m² (le rayon au carré) par une dimension en m (la hauteur). Voici pour finir à quoi ressemblent les graphiques d’analyse des résdius de ce dernier modèle :

chart$residuals(trees_lm8)

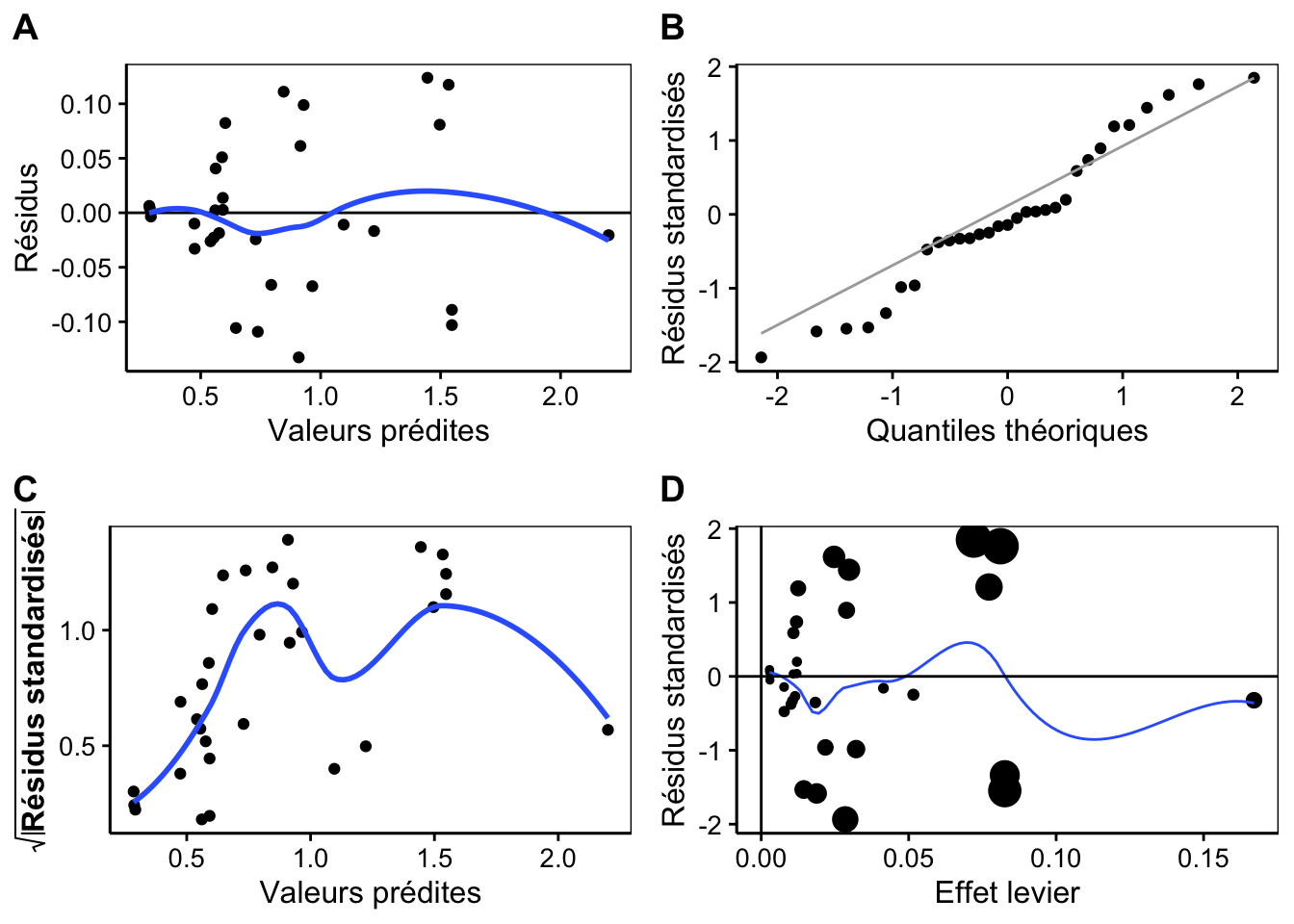
Clairement, nous aurions pu nous économiser de nombreux essais si nous étions partis directement sur cette piste-là. Malheureusement, la biologie fait intervenir souvent un ensemble de mécanismes (bio)chimiques et physiques qui rendent la compréhension mécanistique du phénomène difficile, voire impossible. Heureusement, les modèles empiriques sont également utiles à condition d’être conscient de leurs limites qui impliquent de ne pas chercher à interpréter les termes et les paramètres comme autant d’indicateurs des mécanismes responsables de la distribution des données et sans tirer de conclusions au delà de la relation entre variables (pas d’établissement de causalité sur base d’une régression, jamais).