1.3 Outils de diagnostic
Une fois la meilleure droite de régression obtenue, le travail est loin d’être terminé. Il se peut que le nuage de point ne soit pas tout-à-fait linéaire, que sa dispersion ne soit pas homogène, que les résidus n’aient pas une distribution normale, qu’il existe des valeurs extrêmes aberrantes, ou qui “tirent la droite vers elle” de manière excessive (points trop influents).
Nous allons maintenant devoir diagnostiquer ces possibles problèmes. L’analyse des résidus permet de le faire. Ensuite, si deux ou plusieurs modèles sont utilisable, il nous faut décider lequel conserver. Enfin, nous pouvons aussi calculer et visualiser l’enveloppe de confiance du modèle (une enveloppe qui reprend le “vrai” modèle à un degré de confiance spécifié, souvent 95%) et extraire une série d’informations liées à notre modèle de manière réutilisable dans R.
1.3.1 Analyse des résidus
Le tableau numérique obtenu à l’aide de summary() peut faire penser que l’étude d’une régression linéaire se limite à examiner quelques valeurs numériques et divers tests d’hypothèses associés. C’est un premier pas, mais c’est oublier que la technique est essentiellement visuelle. Le graphique du nuage de points avec la droite superposée est un premier outil diagnostic visuel indispensable, mais il n’est pas le seul ! Plusieurs graphiques spécifiques existent pour mettre en évidence diverses propriétés des résidus qui peuvent révéler des problèmes. Leur inspection est indispensable et s’appelle l’analyse des résidus. Les différents graphiques sont faciles à obtenir à partir des snippets dans RStudio.
Le premier de ces graphique permet de vérifier la distribution homogène des résidus. Dans une bonne régression, nous aurons une distribution équilibrée de part et d’autre du zéro sur l’axe y. Que pensez-vous de notre graphique d’analyse des résidus ? Nous avons une valeur plus éloignée du zéro qui est mise en avant par la courbe de tendance en bleu qui montre l’influence générale des résidus.
#plot(lm., which = 1)
lm. %>.%
chart(broom::augment(.), .resid ~ .fitted) +
geom_point() +
geom_hline(yintercept = 0) +
geom_smooth(se = FALSE, method = "loess", formula = y ~ x) +
labs(x = "Fitted values", y = "Residuals") +
ggtitle("Residuals vs Fitted")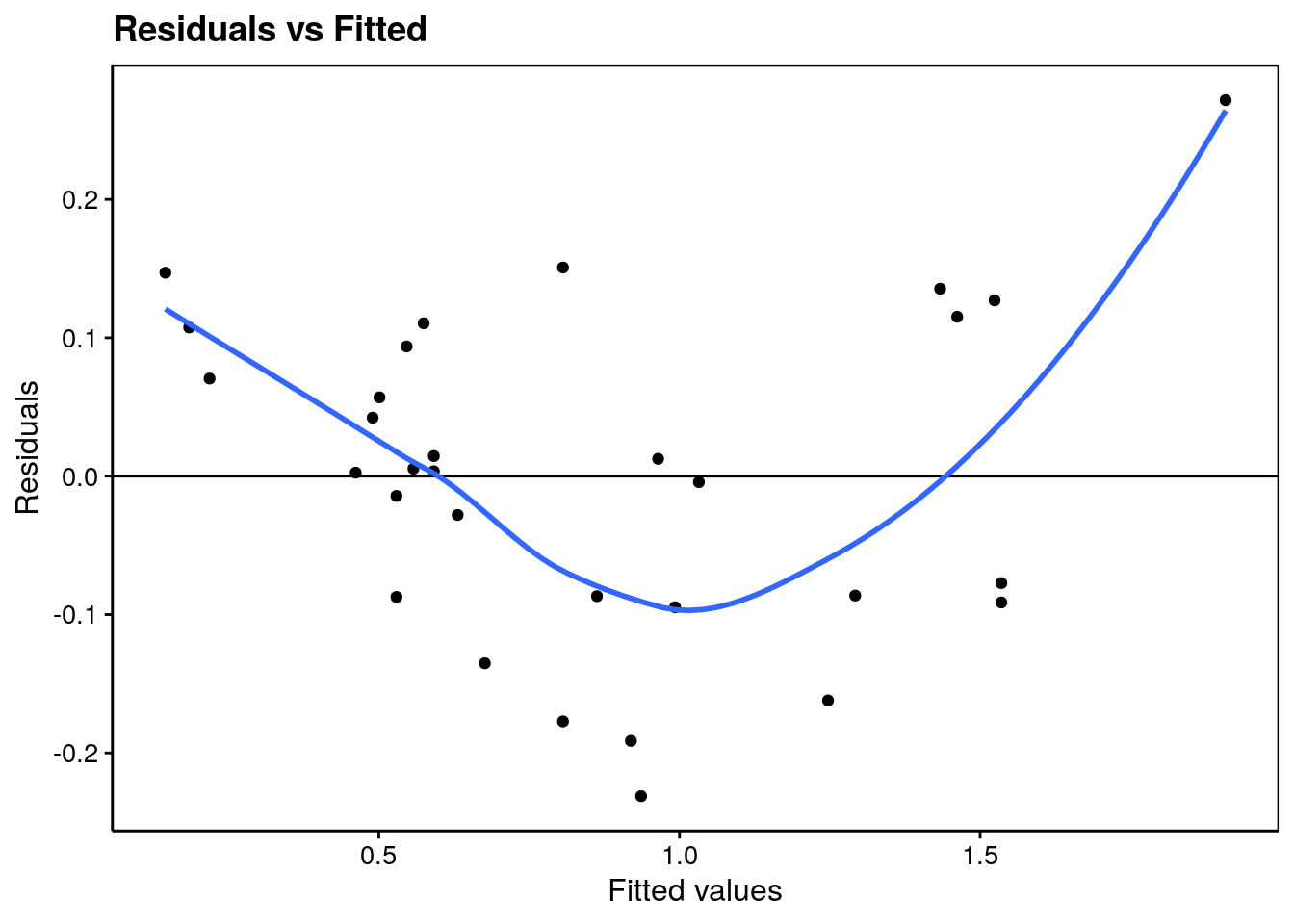
Le second graphique permet de vérifier la normalité des résidus (comparaison par graphique quantile-quantile à une distribution Normale).
#plot(lm., which = 2)
lm. %>.%
chart(broom::augment(.), aes(sample = .std.resid)) +
geom_qq() +
geom_qq_line(colour = "darkgray") +
labs(x = "Theoretical quantiles", y = "Standardized residuals") +
ggtitle("Normal Q-Q")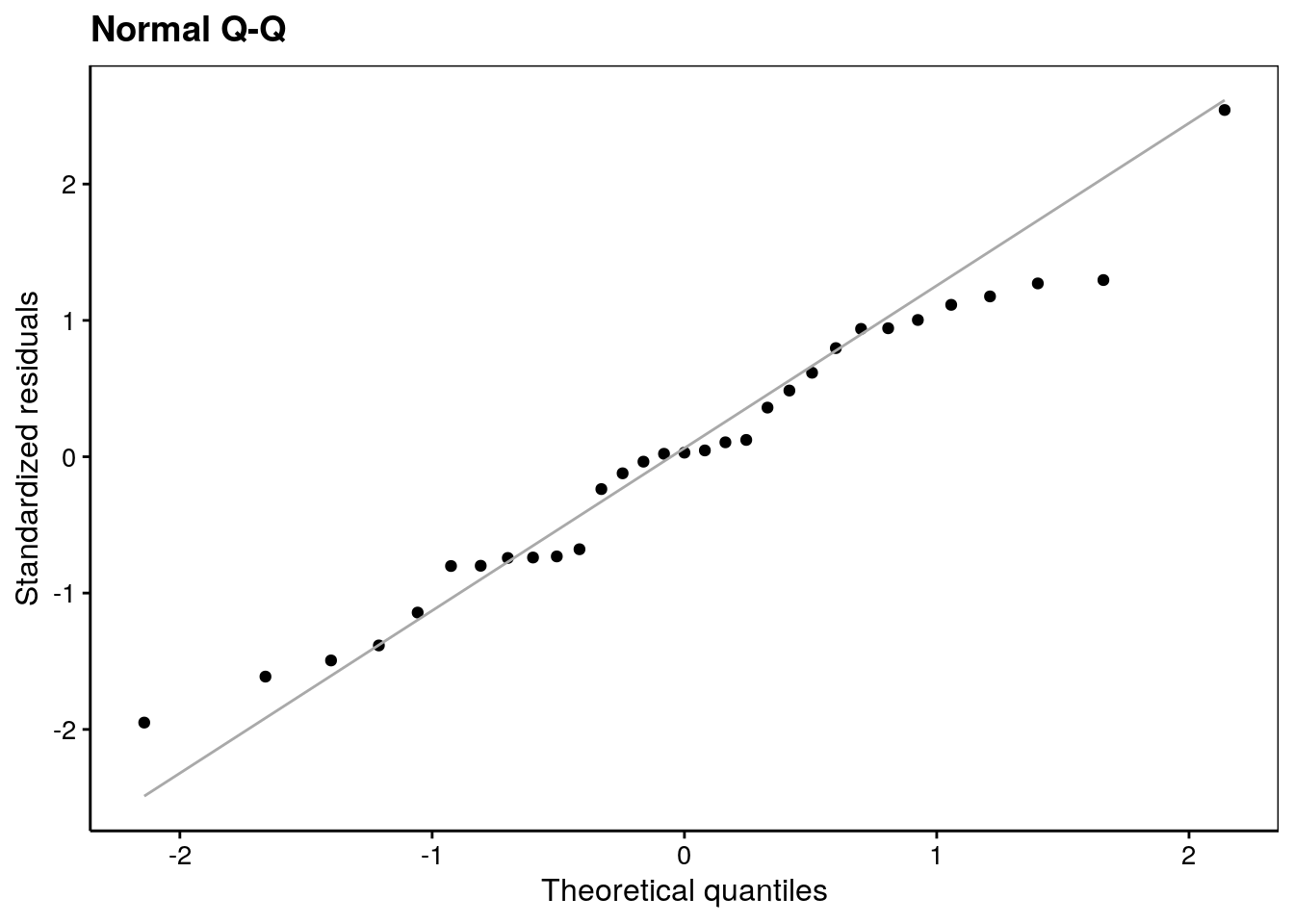
Le troisième graphique va standardiser les résidus, et surtout, en prendre la racine carrée. Cela a pour effet de superposer les résidus négatifs sur les résidus positifs. Nous y diagnostiquons beaucoup plus facilement des problèmes de distribution de ces résidus en complément de ce que le graphique quantile-quantile précédent montre. A nouveau, nous observons qu’une valeur influence fortement la régression en haut à droite sur le graphique.
#plot(lm., which = 3)
lm. %>.%
chart(broom::augment(.), sqrt(abs(.std.resid)) ~ .fitted) +
geom_point() +
geom_smooth(se = FALSE, method = "loess", formula = y ~ x) +
labs(x = "Fitted values",
y = expression(bold(sqrt(abs("Standardized residuals"))))) +
ggtitle("Scale-Location")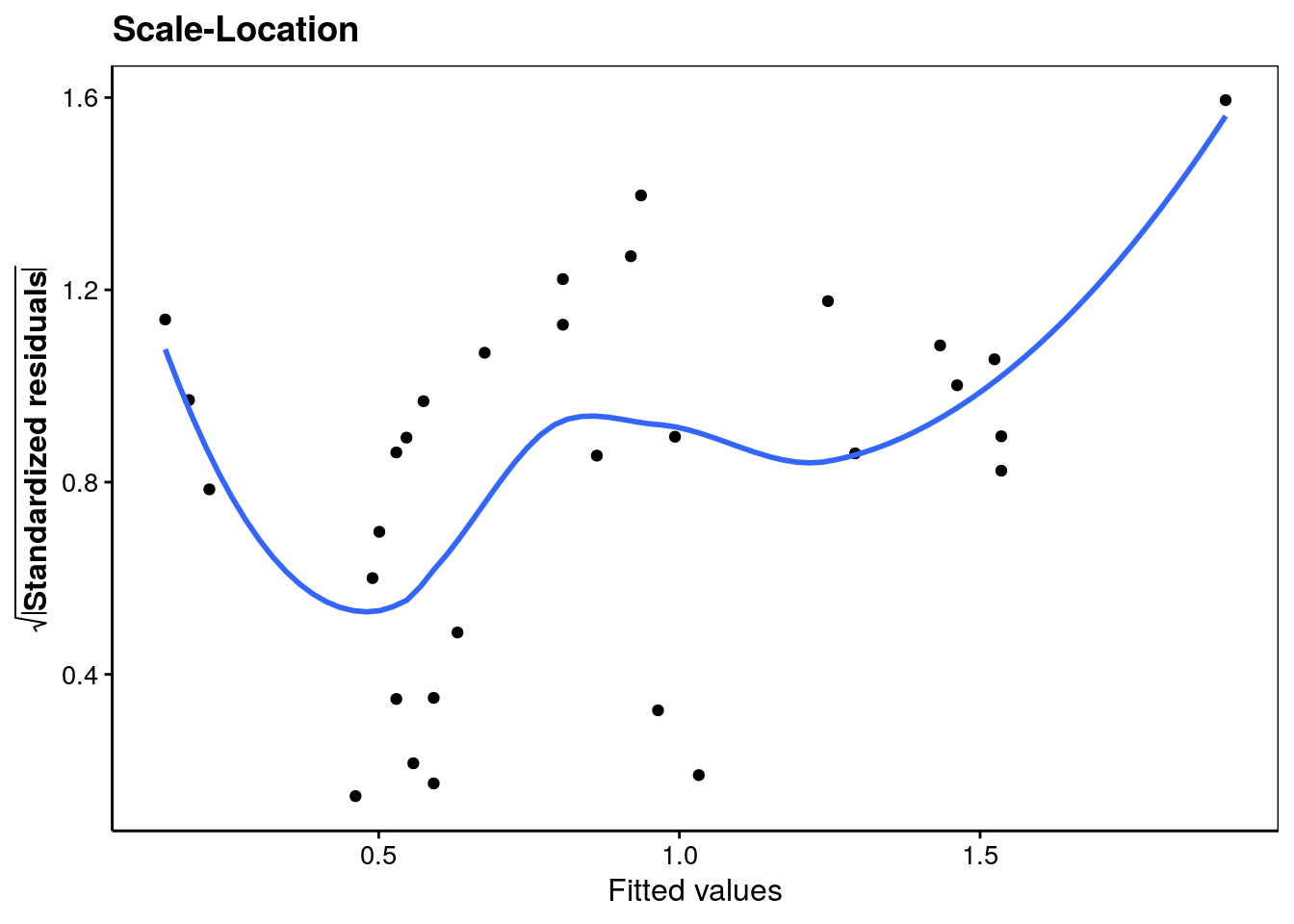
Le quatrième graphique d’analyse des résidus met en évidence l’influence des individus sur la régression linéaire. Effectivement, la régression linéaire est sensible aux valeurs extrêmes. Nous pouvons observer que nous avons une valeur qui influence fortement notre régression. On utilise pour ce faire la distance de Cook que nous ne détaillerons pas dans le cadre de ce cours.
#plot(lm., which = 4)
lm. %>.%
chart(broom::augment(.), .cooksd ~ seq_along(.cooksd)) +
geom_bar(stat = "identity") +
geom_hline(yintercept = seq(0, 0.1, by = 0.05), colour = "darkgray") +
labs(x = "Obs. number", y = "Cook's distance") +
ggtitle("Cook's distance")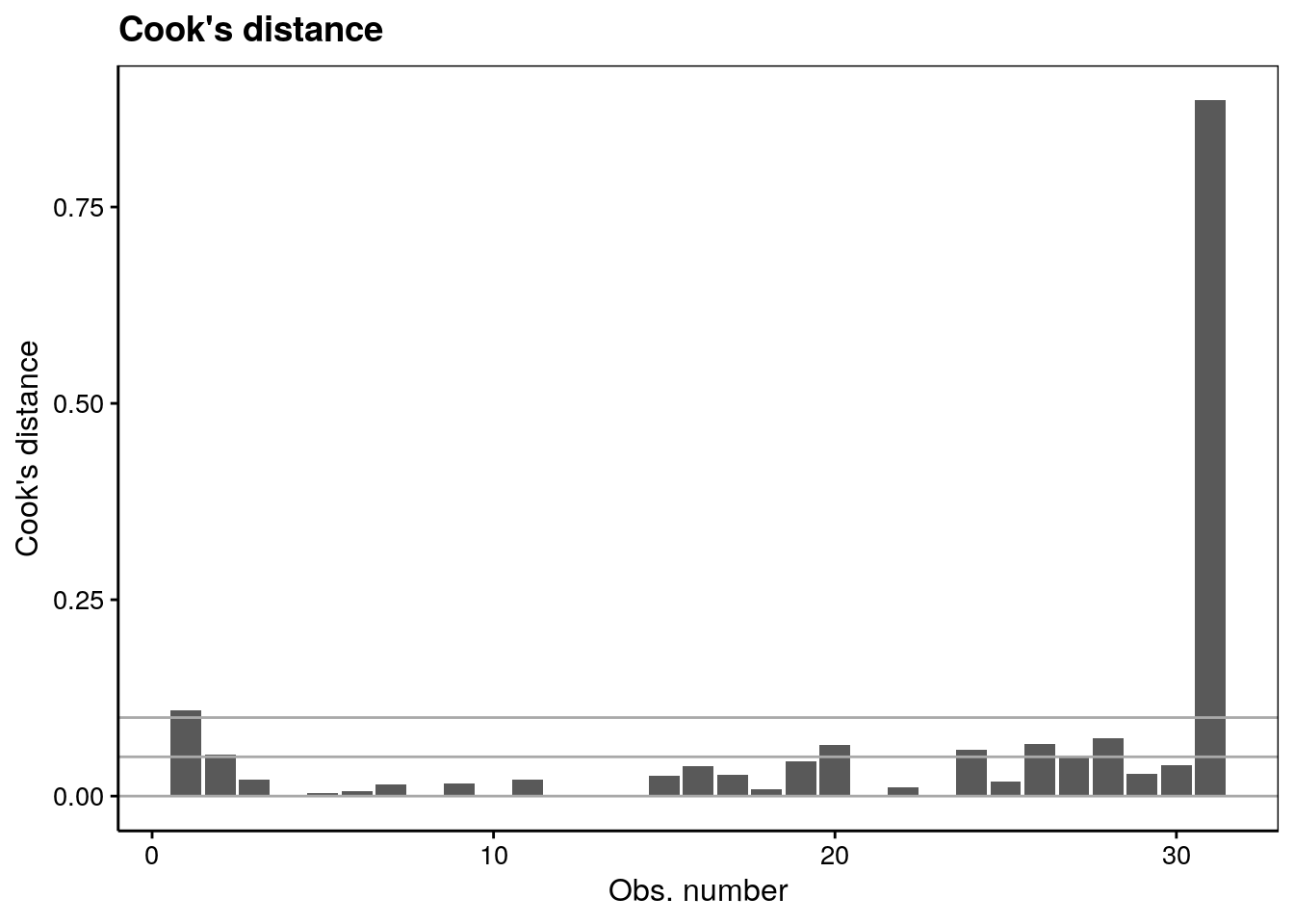
Le cinquième graphique utilise l’effet de levier (Leverage en anglais) qui met également en avant l’influence des individus sur notre régression. Il répond à la question suivante : “est-ce qu’un ou plusieurs points sont tellement influents qu’ils tirent la droite de régression vers eux de manière abusive ?” Nous avons à nouveau une valeur qui influence fortement notre modèle.
#plot(lm., which = 5)
lm. %>.%
chart(broom::augment(.), .std.resid ~ .hat %size=% .cooksd) +
geom_point() +
geom_smooth(se = FALSE, size = 0.5, method = "loess", formula = y ~ x) +
geom_vline(xintercept = 0) +
geom_hline(yintercept = 0) +
labs(x = "Leverage", y = "Standardized residuals") +
ggtitle("Residuals vs Leverage")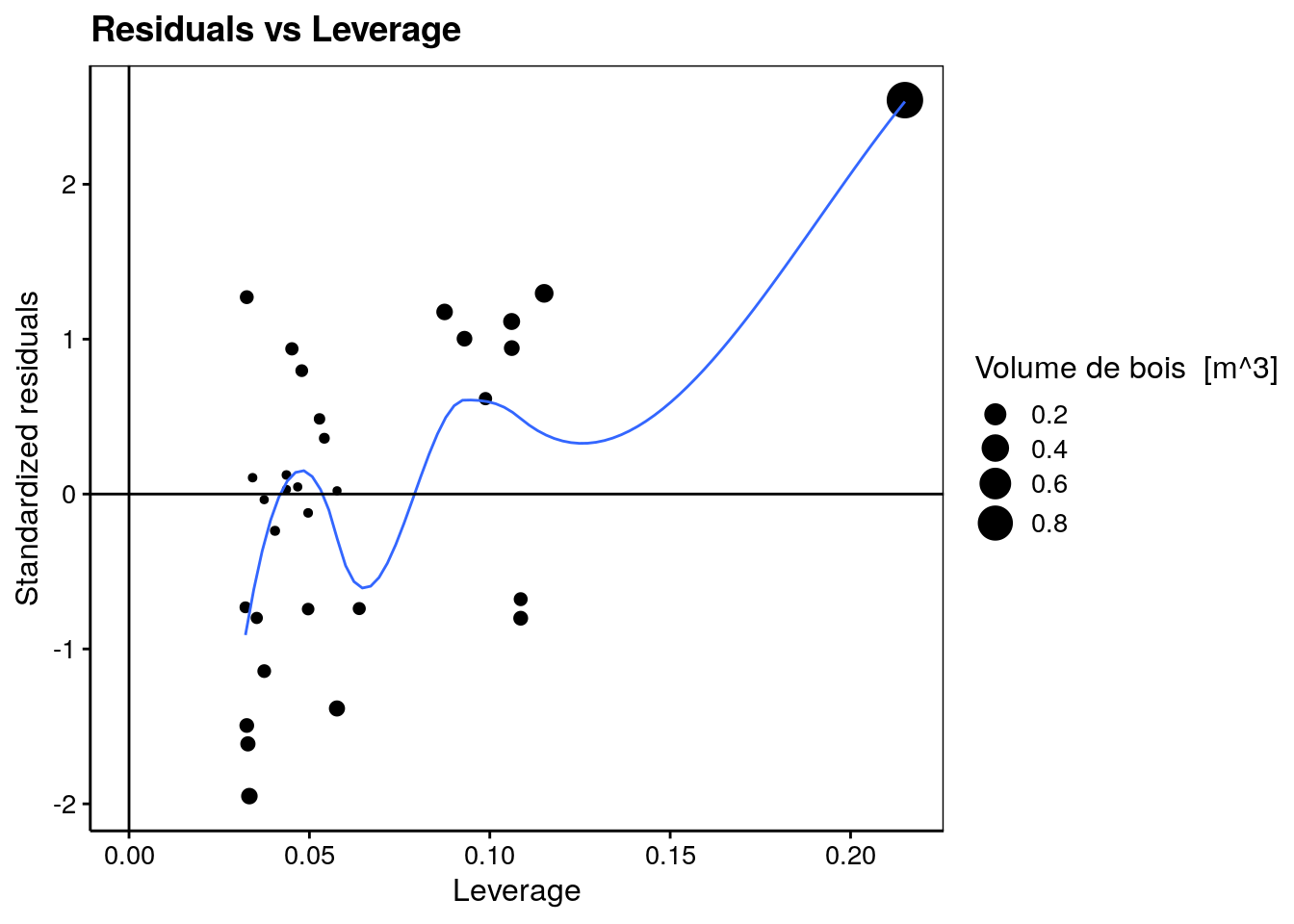
Le sixième graphique met en relation la distance de Cook et l’effet de levier. Notre unique point d’une valeur supérieur à 0.5m de diamètre influence fortement notre modèle, et est dons clairement individualisé sur ce dernier graphique.
#plot(lm., which = 6)
lm. %>.%
chart(broom::augment(.), .cooksd ~ .hat %size=% .cooksd) +
geom_point() +
geom_vline(xintercept = 0, colour = NA) +
geom_abline(slope = seq(0, 3, by = 0.5), colour = "darkgray") +
geom_smooth(se = FALSE, size = 0.5, method = "loess", formula = y ~ x) +
labs(x = expression("Leverage h"[ii]), y = "Cook's distance") +
ggtitle(expression("Cook's dist vs Leverage h"[ii] / (1 - h[ii])))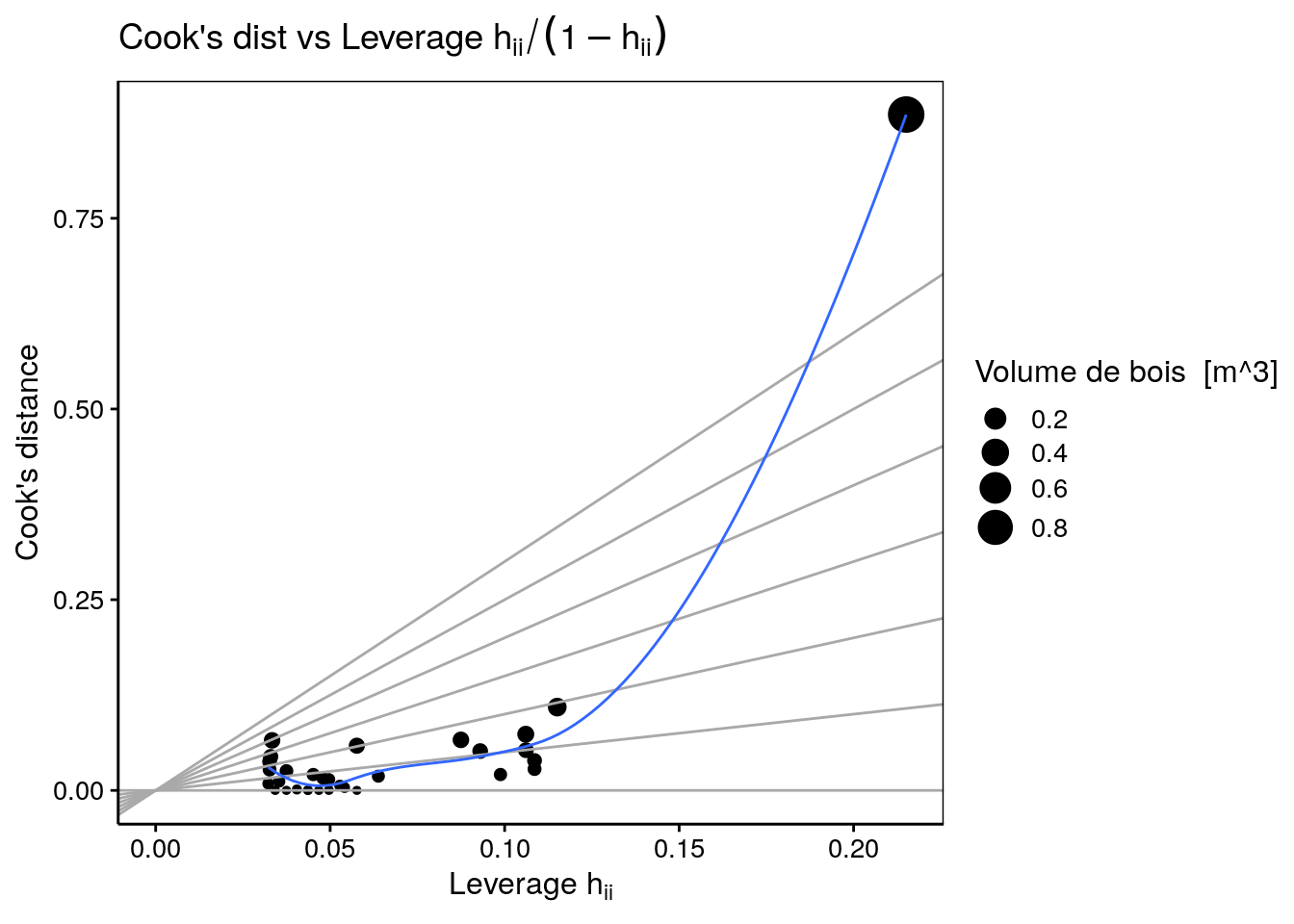
A l’issue de l’analyse des résidus, nous observons donc différents problèmes qui suggèrent que le modèle choisi n’est peut être pas le plus adapté. Nous comprendrons pourquoi plus loin, mais à ce stade si vous avez compris et vous sentez capable d’identifier les problèmes à l’aide de ces graphiques de diagnostic, c’est suffisant.
À vous de jouer !
Effectuez maintenant les exercices du tutoriel B01Lb_reglin1 (Régression linéaire simple).
BioDataScience2::run("B01Lb_reglin1")Pièges et astuces : extrapolation
Notre régression linéaire a été réalisée sur des cerisiers noirs dont le diamètre est compris entre 0.211 et 0.523 mètre. Pensez-vous qu’il soit acceptable de prédire des volumes de bois pour des arbres dont le diamètre est inférieur ou supérieur aux valeurs extrêmes de notre jeu de données d’apprentissage (extrapolation) ?
Utilisons notre régression linéaire afin de prédire huit volumes de bois à partir d’arbres dont le diamètre varie entre 0.1 et 0.7m.
Ajoutons une variable pred qui contient les prédictions en volume de bois d’après notre meilleur modèle linéaire. Observez-vous un problème particulier sur base du tableau obtenu ?
# diameter pred
# 1 0.1000000 -0.482324424
# 2 0.1857143 0.002092891
# 3 0.2714286 0.486510206
# 4 0.3571429 0.970927522
# 5 0.4428571 1.455344837
# 6 0.5285714 1.939762152
# 7 0.6142857 2.424179468
# 8 0.7000000 2.908596783Il est peut-être plus simple de voir le problème sur un graphique en nuage de points. Pour un diamètre de 0.1857143 m de diamètre, le volume de bois est de 0 m3, mis en avant par l’intersection des lignes pointillées bleues.
chart(data = trees, volume~diameter) +
geom_hline(yintercept = 0, linetype = "dashed", color = "grey") +
geom_vline(xintercept = new$diameter[2], linetype = "twodash", color = "blue") +
geom_hline(yintercept = new$pred[2], linetype = "twodash", color = "blue") +
geom_point() +
geom_abline(aes(intercept = lm.$coefficients[1], slope = lm.$coefficients[2])) +
geom_point(data = new, f_aes(pred~diameter), color = "red") 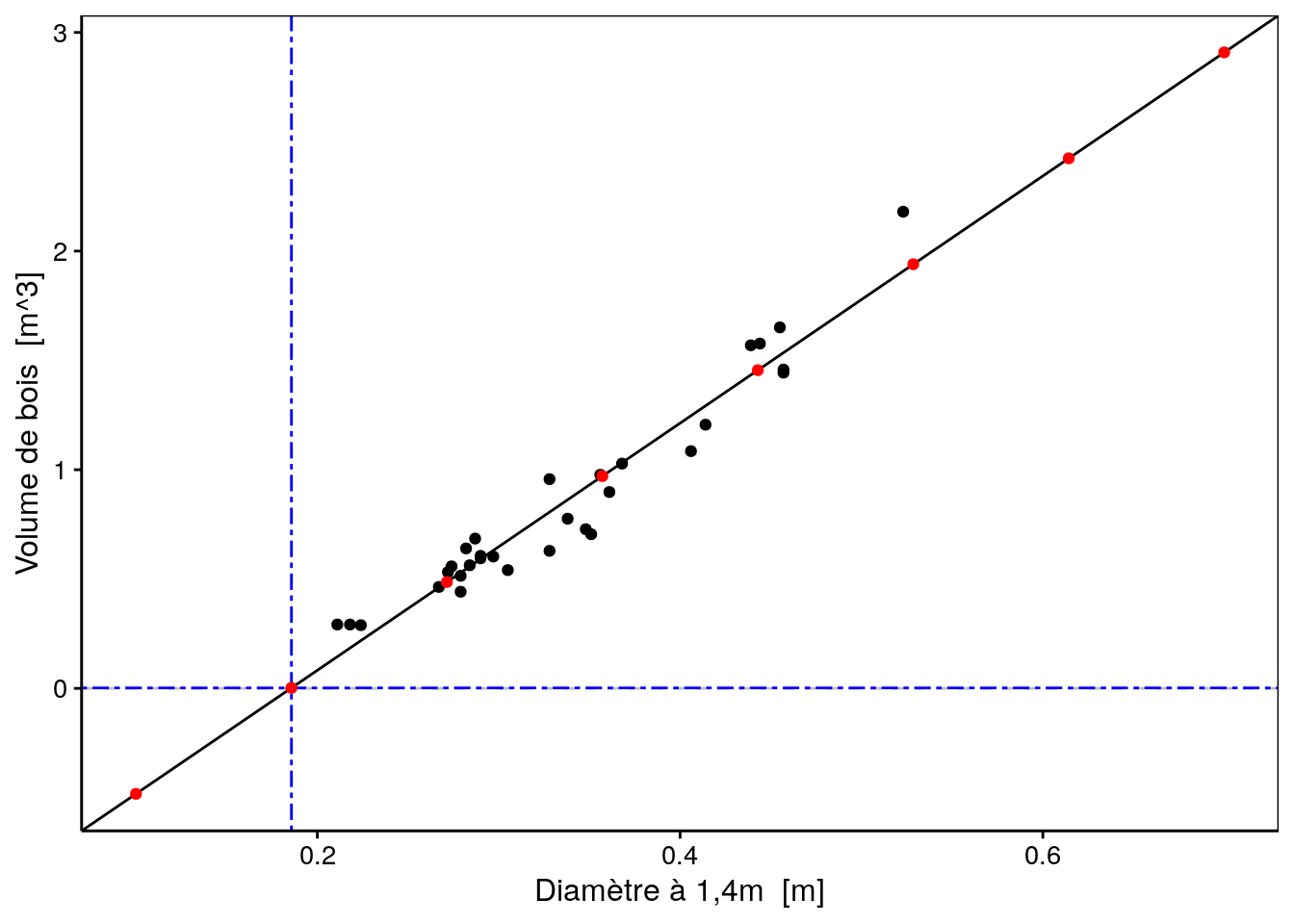
Le volume de bois prédit est même négatif pour des arbres encore plus petits ! Notre modèle est-il alors complètement faux ? Rappelons-nous qu’un modèle est nécessairement une vision simplifiée de la réalité. En particulier, notre modèle a été entraîné avec des données comprises dans un intervalle. Il est alors valable pour effectuer des interpolations à l’intérieur de cet intervalle mais ne peut pas être utilisé pour effectuer des extrapolations en dehors, comme nous venons de le faire.
trees %>.%
modelr::add_predictions(., lm.) -> trees
chart(data = trees, volume~diameter) +
geom_point() +
geom_line(f_aes(pred ~ diameter))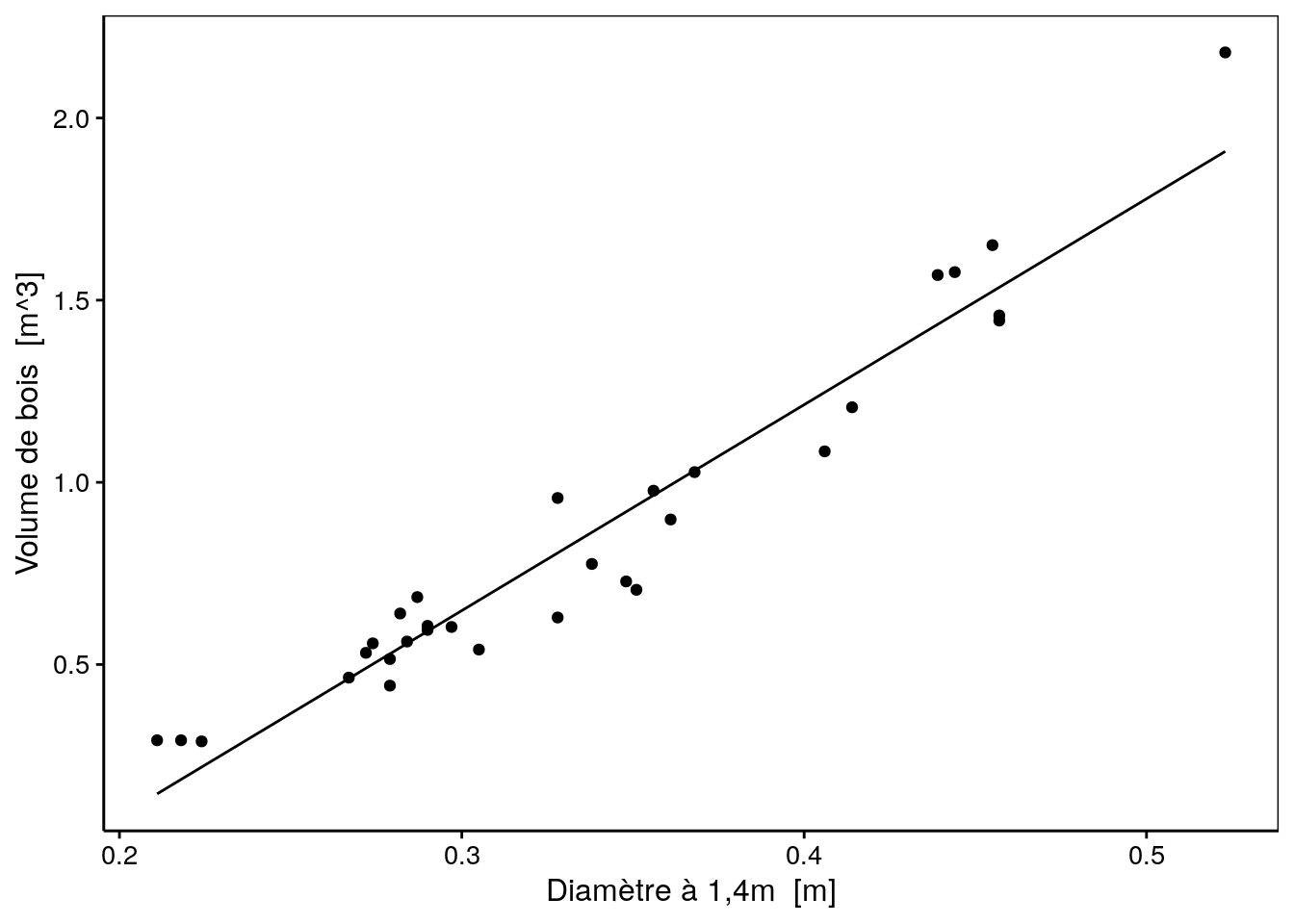
Pièges et astuces : significativité fortuite
Gardez toujours à l’esprit qu’il est possible que votre jeu de données donne une régression significative, mais purement fortuite. Les données supplémentaires de test devraient alors démasquer le problème. D’où l’importance de vérifier/valider votre modèle.
Le principe de parcimonie veut que l’on ne teste pas toutes les combinaisons possibles deux à deux des variables d’un gros jeu de données, mais que l’on restreigne les explorations à des relations qui ont un sens biologique afin de minimiser le risque d’obtenir une telle régression de manière fortuite.
1.3.2 Enveloppe de confiance
De même que l’on peut définir un intervalle de confiance dans lequel la moyenne d’un échantillon se situe avec une probabilité donnée, il est aussi possible de calculer et de tracer une enveloppe de confiance qui indique la région dans laquelle le “vrai” modèle se trouve avec une probabilité donnée (généralement, on choisi cette probabilité à 95%). Voici ce que cela donne en utilisant la fonction stat_smooth() pour ajouter cette enveloppe de confiance sur le graphique :
lm. %>.% (function(lm, model = lm[["model"]], vars = names(model))
chart(data = model, aes_string(x = vars[2], y = vars[1])) +
geom_point() +
stat_smooth(method = "lm", formula = y ~ x))(.)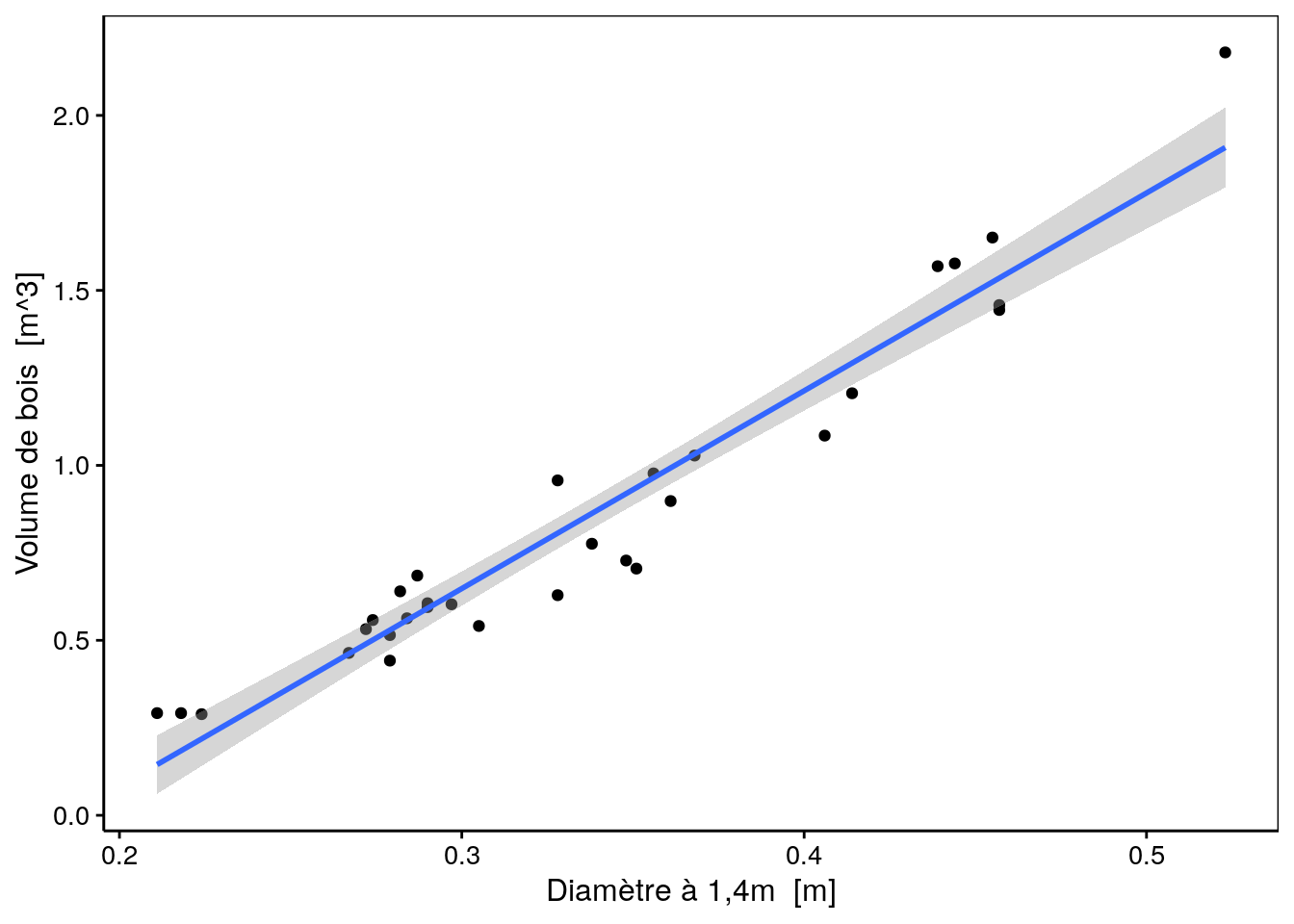
Cette enveloppe de confiance est en réalité basée sur l’écart type conditionnel (écart type de \(y\) sachant quelle est la valeur de \(x\)) qui se calcule comme suit :
\[s_{y|x}\ =\ \sqrt{ \frac{\sum_{i = 0}^n\left(y_i - \hat y_i\right)^2}{n-2}}\]
A partir de là, il est possible de définir également un intervalle de confiance conditionnel à \(x\) :
\[CI_{1-\alpha}\ =\ \hat y_i\ \ \pm \ t_{\frac{\alpha}{2}}^{n-2} \frac{s_{y|x}\ }{\sqrt{n}}\]
C’est cet intervalle de confiance conditionnel qui est matérialisé par l’enveloppe de confiance autour de la droite de régression représentée sur le graphique précédent.
1.3.3 Extraire les données d’un modèle
La fonction tidy() du package broom extrait facilement et rapidement sous la forme d’un tableau différentes valeurs associées à la paramétrisation de notre régression linéaire (informations relatives aux paramètres du modèle). Notez que vous êtes censé renommer DF en quelque chose de plus explicite et changer lm. pour le nom que vous avez donné à votre objet lm.
# # A tibble: 2 x 5
# term estimate std.error statistic p.value
# <chr> <dbl> <dbl> <dbl> <dbl>
# 1 (Intercept) -1.05 0.0955 -11.0 7.85e-12
# 2 diameter 5.65 0.276 20.4 9.09e-19Pour extraire facilement et rapidement sous la forme d’un tableau des valeurs numériques servant au diagnostic de la qualité d’ajustement d’un modèle, nous pouvons aussi utiliser la fonction glance() du même package broom.
# # A tibble: 1 x 11
# r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
# <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
# 1 0.935 0.933 0.121 418. 9.09e-19 2 22.6 -39.2 -34.9
# # … with 2 more variables: deviance <dbl>, df.residual <int>Des snippets sont à votre disposition pour ces deux fonctions :
... -> models ..m -> .models tools .mt -> .mtmoddf... -> models ..m -> .models tools .mt -> .mtpardf
À vous de jouer !
Réalisez l’assignation B01Ga_reglin1.
Si vous êtes un utilisateur non enregistré ou que vous travaillez en dehors d’un cours, faites un “fork” de ce dépôt.
Voyez les explications dans le fichier README.md.